
Beschränkte Variation
In der Analysis ist eine Funktion von beschränkter Variation (beschränkter Schwankung), wenn ihre totale Variation (totale Schwankung) endlich ist, sie also in gewisser Weise nicht beliebig stark oszilliert. Diese Begriffe hängen eng mit der Stetigkeit und der Integrierbarkeit von Funktionen zusammen.
Der Raum aller Funktionen von beschränkter Variation auf dem Gebiet
wird mit
bezeichnet.
Das Konzept geht auf Camille Jordan zurück.
Reelle Funktionen
Definition
Die totale Variation einer reellwertigen
Funktion ,
die auf einem abgeschlossenen Intervall definiert ist, ist das Supremum
wobei dieses Supremum über alle möglichen Partitionen
des Intervalls
gebildet wird. Das hier angegebene
hängt von
ab.
Genau die stetigen Funktionen von beschränkter Variation sind Riemann-Stieltjes-integrierbar.
Deshalb kann
mit einer Halbnorm ausgestattet werden:
.
Dieses Supremum wird über alle Funktionen
mit kompaktem
Träger
und Funktionswerten im Intervall
gebildet.
Die Halbnorm stimmt mit dem Supremum, das die beschränkte Variation definiert, überein.
Beispiel
.svg.png)
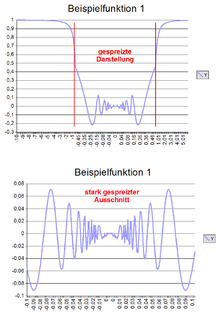
Ein einfaches Beispiel für eine unbeschränkte Variation ist die
Funktion
in der Nähe von
.
Es ist anschaulich einsichtig, dass der Wert des Quotienten
für
mit zunehmender Annäherung an 0 immer schneller gegen ∞ anwachsen wird, und
damit der Sinus
dieses Werts dabei unendlich viele Schwingungen durchlaufen wird. Dies zeigt das
Bild rechts.
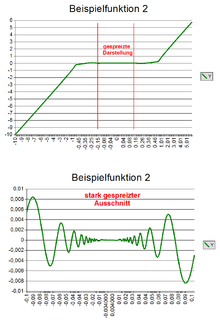
Die Funktion
ist ebenfalls nicht von beschränkter Schwankung im Intervall [0, 1], im Gegensatz zur Funktion:
.
Hier wird die Variation des Sinusterms, die für
stark zunimmt, durch die zusätzliche Potenz genug gedämpft.
Erweiterungen
Diese Definition kann auch für komplexwertige Funktionen verwendet werden.
BV-Funktionen in mehreren Variablen
Funktionen von beschränkter Variation, oder -Funktionen,
sind Funktionen, deren distributionelle
Ableitungen endliche vektorwertige
Radonmaße sind. Genauer:
Definition
Sei
eine offene Teilmenge von
.
Eine Funktion
ist von beschränkter Variation oder Element von
,
wenn ihre distributionelle Ableitung ein endliches, signiertes, vektorwertiges
Radonmaß ist. D.h., es existiert
,
so dass
gilt.
Zusammenhang mit rektifizierbaren Wegen
Eine stetige Funktion
kann auch als Weg
im metrischen
Raum
aufgefasst werden. Es gilt, dass
genau dann von beschränkter Variation ist, wenn
>
ein rektifizierbarer
Weg ist, also eine endliche Länge hat.
Zusammenhang mit der Maßtheorie
In der Maßtheorie
sind die reell-/komplexwertigen Funktionen von beschränkter Variation genau die
Verteilungsfunktionen
von signierten/komplexen Borelmaßen
auf .


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.11. 2020