Komplexer Schubmodul

Der komplexe Schubmodul $G^{*}$ beschreibt in der Schwingungsrheometrie das Verhalten viskoelastischer Körper bei einer oszillierenden Scherbelastung. Er verknüpft die auf die Probe einwirkende Schubspannung $\tau$ mit der resultierenden Scherdeformation $\gamma$ .

Der komplexe Schubmodul kann messtechnisch relativ einfach mit einem Rheometer (für Flüssigkeiten) und durch Dynamisch-mechanische Analyse (für Feststoffe) bestimmt werden. Die Veränderung des komplexen Schubmoduls bei Variation von Amplitude, Frequenz oder anderen Parametern wie der Temperatur gibt Aufschluss über die Eigenschaften des Materials. So kann z.B. der lineare Bereich ermittelt, auf die Molekülstruktur geschlossen oder ein Vernetzungsvorgang untersucht werden.

Speicher- und Verlustmodul

Allgemein hat der komplexe Schubmodul die Form einer komplexen Zahl:

$G^{*}=G'+i\cdot G''$

mit

dem Speichermodul (Realteil), der für den elastischen Anteil steht. Er ist proportional zu dem Anteil der Deformationsenergie, der im Material gespeichert wird und nach Entlastung wieder aus dem Material gewonnen werden kann.
dem Verlustmodul (Imaginärteil), der für den viskosen Anteil steht. Er entspricht dem Verlustanteil der Energie, welcher durch innere Reibung in Wärme umgewandelt wird.

Der Quotient aus G'' und ist der Verlustfaktor $\tan \delta$ :

$\tan \delta = \frac{G''}{G'}$

Er nimmt für einen ideal elastischen Körper den Wert 0 an $\left(G''=0\Rightarrow \tan \delta =0\right),$
für einen ideal viskosen Körper geht er gegen unendlich $\left(G'\to 0\Rightarrow \tan \delta \to \infty \right).$

Grundlagen

Prinzip der Scherung

Maxwell-Körper

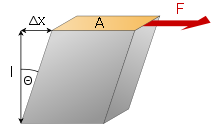
Erfährt ein Körper eine Scherung

$\gamma =\tan \theta ={\frac {\Delta x}{l}}$ ,

so ist dazu die Schubspannung

$\tau ={\frac {F}{A}}$

notwendig

mit

$\theta$ - Scherwinkel
$\Delta x$ - Verformungsweg
- Dicke des betrachteten Körpers
- Verformungskraft
- Fläche.

Das Verhalten eines viskoelastischen Materials, d.h. der Zusammenhang zwischen Schubspannung und Scherung, kann durch rheologische Modellkörper nachgebildet werden, die sich zusammensetzen aus

Federn (Hooke-Elementen), die den rein elastischen Anteil darstellen. Hier ist die Schubspannung $\tau _{H}$ über den Schubmodul mit der Scherung $\gamma _{H}$ verbunden:

$\tau _{H}=G\cdot \gamma _{H}$

Setzt man den Körper einer sinusförmigen Scherung mit Amplitude ${\hat \gamma }$ und Kreisfrequenz $\omega$ aus:

$\gamma (t)={\hat \gamma }\cdot \sin(\omega t),$

so gilt im elastischen Zweig:

$\tau _{H}(t)=G\cdot {\hat \gamma }\cdot \sin(\omega t)$

Bei einem ideal elastischen Körper hat also auch die Schubspannung einen sinusförmigen Verlauf, und zwar in Phase mit der Scherung: im Nulldurchgang der Schwingung erfährt der Körper keine Verformung und deswegen ist auch keine Schubspannung zur Überwindung der Rückstellkraft notwendig. In der Amplitude ist dagegen der Körper maximal verformt, dann ist auch die Rückstellkraft am größten.

Dämpfungszylindern (Newton-Elementen mit einer newtonschen Flüssigkeit) für den ideal viskosen Anteil. Hier ist die Schubspannung $\tau _{N}$ über die Viskosität $\eta$ mit der Schergeschwindigkeit ${\dot \gamma }_{N}$ verbunden, also mit der ersten Ableitung der Scherung:

${\begin{aligned}\tau _{N}&=\eta \cdot {\dot \gamma }_{N}\\&=\eta \cdot ({\hat \gamma }\cdot \sin(\omega t))'\\&=\eta \cdot {\hat \gamma }\cdot \omega \cdot \cos(\omega t)\end{aligned}}$

Ein ideal viskoser Körper weist also einen um 90° phasenverschobenen Verlauf der Schubspannung auf: im Nulldurchgang der Deformation ist die Änderung der Verformung am größten, deswegen ist auch der von der Flüssigkeit entgegengesetzte Widerstand, der überwunden werden muss, am größten. In der Amplitude kehrt sich die Bewegungsrichtung um, die Schergeschwindigkeit und damit auch die Schubspannung werden für einen Moment zu Null.

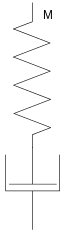
Einfache Modelle zur Beschreibung eines viskoelastischen Festkörpers sind z.B.

das Maxwell-Modell, d.h. die Hintereinanderschaltung einer Feder mit einem Dämpfungselement, oder
das Kelvin-Modell, d.h. die Parallelschaltung einer Feder mit einem Dämpfungszylinder.

Herleitung für den Kelvin-Körper

Kelvin-Körper

Bei einem Kelvin-Körper ist wegen der Parallelschaltung die Scherung $\gamma$ in beiden Zweigen dieselbe, die Gesamtschubspannung setzt sich dagegen aus den Schubspannungen in Hooke- und Newton-Element zusammen:

${\begin{alignedat}{2}\gamma (t)&=\gamma _{H}(t)&&=\gamma _{N}(t)\\\tau (t)&=\tau _{H}(t)&&+\tau _{N}(t)\\&=G\cdot {\hat \gamma }\cdot \sin(\omega t)&&+\eta \cdot \omega \cdot {\hat \gamma }\cdot \cos(\omega t)\end{alignedat}}$

Rein formal entsprechen die Beziehungen der Parallelschaltung eines ohmschen Widerstandes mit einer Induktivität in der Elektrizitätslehre. Wie dort kann die Gleichung mit einem Zeigerdiagramm umgeformt werden zu:

$\tau (t)=|G^{*}|\cdot {\hat \gamma }\cdot \sin(\omega t+\delta )$

mit

$|G^{*}|={\sqrt {G^{2}+(\eta \cdot \omega )^{2}}}$

und

$\tan \delta ={\frac {\eta \cdot \omega }{G}}$

Die Schubspannung ist also um den Phasenwinkel $\delta$ , der einen Wert zwischen 0° und 90° annehmen kann, gegenüber der Scherung verschoben.

In Analogie zur komplexen Wechselstromrechnung können die Größen auch mit komplexen Funktionen beschrieben werden:

$\gamma ^{*}={\hat \gamma }\cdot e^{{i\omega t}}\qquad \qquad \qquad \qquad \qquad {\text{mit}}\quad \gamma (t)=\operatorname {Re}(\gamma ^{*})$

$\tau ^{*}=(G\cdot {\hat \gamma }+i\cdot \eta \cdot \omega \cdot {\hat \gamma })\cdot e^{{i\omega t}}\qquad {\text{mit}}\quad \tau (t)=\operatorname {Re}(\tau ^{*})$

Dann ist der komplexe Schubmodul $G^{*}$ der Quotient aus komplexer Schubspannung und komplexer Scherung:

$G^{*}={\frac {\tau ^{*}}{\gamma ^{*}}}={\frac {(G\cdot {\hat \gamma }+i\cdot \eta \cdot \omega \cdot {\hat \gamma })\cdot e^{{i\omega t}}}{{\hat \gamma }\cdot e^{{i\omega t}}}}=G+i\cdot \eta \cdot \omega$

Der Kehrwert

$J^{*}={\frac {1}{G^{*}}}={\frac {\gamma ^{*}}{\tau ^{*}}}$

wird als komplexe Nachgiebigkeit bezeichnet.

Komplexe Viskosität

Leitet man $\gamma ^{*}$ ab, so erhält man die komplexe Schergeschwindigkeit:

${\dot \gamma }^{*}={\frac {{\mathrm {d}}({\hat \gamma }\cdot e^{{i\omega t}})}{{\mathrm {d}}t}}={\hat \gamma }\cdot (i\cdot \omega )\cdot e^{{i\omega t}}$

Damit lässt sich die komplexe Viskosität $\eta ^{*}=\eta '+i\cdot \eta ''$ berechnen:

$\eta ^{*}={\frac {\tau ^{*}}{{\dot \gamma }^{*}}}={\frac {G^{*}\cdot \gamma ^{*}}{{\dot \gamma }^{*}}}={\frac {(G'+i\cdot G'')\cdot {\hat \gamma }\cdot e^{{i\omega t}}}{{\hat \gamma }\cdot (i\cdot \omega )\cdot e^{{i\omega t}}}}=\underbrace {{\frac {G''}{\omega }}}_{{\eta '}}+i\cdot \underbrace {\left(-{\frac {G'}{\omega }}\right)}_{{\eta ''}}$

Ihr Betrag ist:

$|\eta ^{*}|={\sqrt {\left({\frac {G''}{\omega }}\right)^{2}+\left({\frac {G'}{\omega }}\right)^{2}}}={\frac {|G^{*}|}{\omega }}$

Aus dem Realteil von $\eta ^{*}$ wird die dynamische Viskosität berechnet:

$Re(\eta ^{*})={\frac {G''}{\omega }}={\frac {\eta \omega }{\omega }}=\eta$

Basierend auf einem Artikel in:

Wikipedia.de