CAT(0)-Raum

CAT(0)-Räume sind ein Begriff aus der Geometrie, mit dem Eigenschaften von Mannigfaltigkeiten nichtpositiver Krümmung auf allgemeine metrische Räume verallgemeinert werden. Ihre definierende Eigenschaft ist, dass Dreiecke dünner sein sollen als Vergleichsdreiecke in der euklidischen Ebene.

Definition

Vergleichsdreiecke

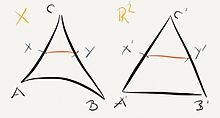
$d(x,y)\leq \parallel x^{\prime }-y^{\prime }\parallel$

Sei (X,d) ein geodätischer metrischer Raum. Ein geodätisches Dreieck $\Delta (a,b,c)$ in ist ein Dreieck mit Ecken $a,b,c\in X$ , dessen drei Seiten Geodäten sind. Zu jedem geodätischen Dreieck $\Delta (a,b,c)$ gibt es ein (bis auf Kongruenz eindeutiges) Vergleichsdreieck $\Delta (a^{\prime },b^{\prime },c^{\prime })$ im $\mathbb R^2$ mit

$d(a,b)=\lVert a^{\prime }-b^{\prime }\rVert ,\ d(a,c)=\lVert a^{\prime }-c^{\prime }\rVert ,\ d(b,c)=\lVert b^{\prime }-c^{\prime }\rVert$ .

Man hat dann eine Vergleichsabbildung

$f:\partial \Delta (a,b,c)\rightarrow \partial \Delta (a^{\prime },b^{\prime },c^{\prime })$ ,

die (zum Beispiel) jedem Punkt auf der Seite (a,b) den entsprechenden Punkt $x^{\prime }$ auf der Seite $(a^{\prime },b^{\prime })$ (d.h. den eindeutigen Punkt mit $\lVert x^{\prime }-a^{\prime }\rVert =d(x,a)$ ) zuordnet, analog für die beiden anderen Seiten.

CAT(0)-Räume

Ein geodätischer metrischer Raum (X,d) ist ein CAT(0)-Raum, wenn zu jedem geodätischen Dreieck $\Delta (a,b,c)$ in mit Vergleichsabbildung $f:\partial \Delta (a,b,c)\rightarrow \partial \Delta (a^{\prime },b^{\prime },c^{\prime })$ die Ungleichung

$d(x,y)\leq \lVert f(x)-f(y)\rVert$ für alle $x,y\in \partial \Delta (a,b,c)$ gilt.

Anschaulich: Jedes geodätische Dreieck ist mindestens so dünn wie sein Vergleichsdreieck.

Beispiele

Einfach zusammenhängende vollständige Riemannsche Mannigfaltigkeiten nichtpositiver Schnittkrümmung sind CAT(0)-Räume. Dazu zählen der euklidische $\mathbb {R} ^{n}$ , der hyperbolische Raum, $SL(n,{\mathbb R})/SO(n)$ , allgemeiner alle symmetrischen Räume ohne kompakten Faktor.
Einfach zusammenhängende vollständige Riemannsche Mannigfaltigkeiten nichtpositiver Schnittkrümmung werden auch als Hadamard-Mannigfaltigkeiten bezeichnet. Vollständige CAT(0)-Räume bezeichnet man als Hadamard-Räume.
Endliche Produkte von CAT(0)-Räumen sind CAT(0)-Räume.
$\mathbb {R}$ -Bäume und euklidische oder hyperbolische Gebäude sind CAT(0)-Räume.
Hilberträume sind CAT(0)-Räume.
Eine zusammenziehbare Mannigfaltigkeit der Dimension $\geq 6$ trägt genau dann eine geodätisch vollständige CAT(0)-Metrik, wenn sie kollabierbar ist.
Satz von Gromov: Ein kubischer Komplex ist genau dann ein CAT(0)-Raum, wenn er einfach zusammenhängend und der Link jeder Ecke ein Fahnenkomplex ist.

Eigenschaften

In einem CAT(0)-Raum lassen sich je zwei Punkte durch eine eindeutige Geodäte verbinden. Die Geodäte hängt stetig von ihren Endpunkten ab.
In CAT(0)-Räumen gilt die Ptolemäische Ungleichung

$d(x,y)d(u,v)\leq d(x,u)d(y,v)+d(x,v)d(y,u)$ für alle $x,y,u,v\in X$ .

Für Geodäten $\gamma _{1},\gamma _{2}:\left[a,b\right]\rightarrow X$ ist die Funktion $d(\gamma _{1}(t),\gamma _{2}(t))$ konvex.
CAT(0)-Räume sind zusammenziehbar.

Geodätischer Rand

Geodätische Strahlen in einem CAT(0)-Raum heißen asymptotisch, wenn sie endlichen Abstand haben. Dies definiert eine Äquivalenzrelation auf der Menge der geodätischen Strahlen. Der Geodätische Rand $\partial _{\infty }X$ des CAT(0)-Raumes (X,d) ist die Menge der Äquivalenzklassen von auf Bogenlänge parametrisierten geodätischen Strahlen.

Jeder Punkt in $\partial _{\infty }X$ lässt sich mit jedem Punkt in durch eine eindeutige Geodäte verbinden. Unterschiedliche Punkte in $\partial _{\infty }X$ müssen sich aber nicht immer durch eine Geodäte verbinden lassen.

Kegel-Topologie

Die Topologie auf (X,d) lässt sich zu einer Topologie auf $X\cup \partial _{\infty }X$ erweitern, so dass gilt: Eine Folge $(x_{n})_{n\in \mathbb {N} }$ konvergiert gegen $p\in \partial _{\infty }X$ genau dann, wenn (für beliebiges $x_{0}\in X$ ) die Folge der $x_{0}$ und $x_{n}$ verbindenden Geodäten lokal gleichmäßig gegen die $x_{0}$ und verbindende Geodäte konvergiert.

Diese Topologie wird als Kegel-Topologie bezeichnet.

Beispiel: Wenn (X,d) eine einfach zusammenhängende, vollständige n-dimensionale Riemannsche Mannigfaltigkeit nichtpositiver Schnittkrümmung ist, dann ist $\partial _{\infty }X$ mit der Kegel-Topologie homöomorph zur (n-1)-dimensionalen Sphäre.

Tits-Metrik

Die Tits-Metrik $d_{T}:\partial _{\infty }X\times \partial _{\infty }X\rightarrow {\mathbb R}$ ist für $p_{1},p_{2}\in \partial _{\infty }X$ definiert durch

$d_{T}(p_{1},p_{2}):=\sup _{{x\in X}}\lim _{{t\rightarrow \infty }}\angle _{x}(\gamma _{1}(t),\gamma _{2}(t))$ ,

wobei $\gamma_1,\gamma_2$ zu $p_{1},p_{2}$ asymptotische Geodäten sind.

Hierbei ist (allgemein für $x,a,b\in X$ ) der Winkel $\angle _{x}(a,b)$ definiert als der Winkel bei $x^{\prime }$ des Vergleichsdreiecks $\Delta (x^{\prime },a^{\prime },b^{\prime })$ im $\mathbb R^2$ .

Die Tits-Metrik induziert im Allgemeinen nicht die Kegel-Topologie auf $\partial _{\infty }X$ .

Beispiele: Falls (X,d) eine einfach zusammenhängende, vollständige Riemannsche Mannigfaltigkeit negativer Schnittkrümmung ist, dann ist $d_{T}(p_{1},p_{2})=\pi$ für alle $p_{1},p_{2}\in \partial _{\infty }X$ , die Tits-Metrik induziert also die diskrete Topologie. Falls $(X,d)=({\mathbb R}^{n},d_{{eukl}})$ der euklidische Raum ist, dann ist $(\partial _{\infty }X,d_{T})$ homöomorph zur Sphäre.

Horosphären

Zu einem Punkt $p\in \partial _{\infty }X$ und einer Geodäte $\gamma :\left[0,\infty \right]\rightarrow X$ mit $\lim _{{t\rightarrow \infty }}\gamma (t)=p$ definiert man die Busemann-Funktion $b_{\gamma }:X\rightarrow {\mathbb R}$ durch

$b_{\gamma }(x):=\lim _{{t\rightarrow \infty }}d(x,\gamma (t))-t$ .

Falls vollständig ist und $\gamma _{1}$ und $\gamma_2$ zwei zu $p\in \partial _{\infty }X$ asymptotische Geodäten sind, dann ist $b_{{\gamma _{1}}}-b_{{\gamma _{2}}}$ konstant. Insbesondere hängt die Zerlegung von in die Niveaumengen von $b_{\gamma }$ nur von $p\in \partial _{\infty }X$ und nicht von der Wahl der zu asymptotischen Geodäte $\gamma$ ab. Die Niveaumengen von $b_{\gamma }(x)$ werden als Horosphären von bezeichnet.

Isometrien

Jede Isometrie $f:X\rightarrow X$ eines vollständigen CAT(0)-Raumes (X,d) fällt in eine der folgenden 3 Klassen:

elliptisch: hat einen Fixpunkt in ,
hyperbolisch: hat keinen Fixpunkt in , lässt aber eine Geodäte invariant,
parabolisch: lässt einen Punkt $p\in \partial _{\infty }X$ und seine Horosphären invariant.

CAT(0)-Gruppen

Eine CAT(0)-Gruppe ist eine Gruppe, die eigentlich diskontinuierlich und kokompakt durch Isometrien auf einem endlich-dimensionalen CAT(0)-Raum wirkt.

Lokale CAT(0)-Räume

Ein vollständiger, zusammenhängender, metrischer Raum heißt lokal CAT(0), wenn jeder Punkt eine Umgebung besitzt, die (mit der eingeschränkten Metrik) ein CAT(0)-Raum ist.

Eine Verallgemeinerung des Satzes von Cartan-Hadamard besagt: wenn ein lokaler CAT(0)-Raum ist, dann gibt es auf der universellen Überlagerung $\widetilde {X}$ eine eindeutige Metrik ${\tilde {d}}$ so dass

die Überlagerung ${\widetilde {X}}\to X$ eine lokale Isometrie ist, und
$({\widetilde {X}},{\tilde {d}})$ ein CAT(0)-Raum ist.

Basierend auf einem Artikel in:

Wikipedia.de