Nernst-Gleichung

Die Nernst-Gleichung (benannt nach Walther Nernst, seltener auch Peterssche Gleichung) beschreibt die Konzentrationsabhängigkeit des Elektrodenpotentials eines Redox-Paares (Ox + z e⁻ $\rightarrow$ Red)

$E=E^{0}+{\frac {RT}{z_{e}F}}\ln {\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}$

Durch Zusammenfassen der Naturkonstanten R, F, dem Umrechnungsfaktor für den natürlichen Logarithmus zum dekadischen Logarithmus und der Festlegung auf eine Temperatur von 25 °C (298 K) vereinfacht sich diese Form zu:

$E=E^{0}+{\frac {8{,}314\ \mathrm {\frac {J}{mol\cdot K}} \cdot 298\ \mathrm {K} \cdot 2{,}303}{z_{e}\cdot 96485{,}336\ \mathrm {\frac {C}{mol}} }}\log {\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}=E^{0}+{\frac {8{,}314\cdot 298\cdot 2{,}303\ \mathrm {J} }{z_{e}\cdot 96485{,}336\ \mathrm {C} }}\log {\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}\approx E^{0}+{\frac {0{,}059\ \mathrm {V} }{z_{e}}}\log {\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}$

	Elektrodenpotential
$E^{0}$	Standardelektrodenpotential
	Universelle oder molare Gaskonstante, R = 8,31447 J mol⁻¹ K⁻¹ = 8,31447 C V mol⁻¹ K⁻¹
	absolute Temperatur (= Temperatur in Kelvin)
$z_{e}$	Anzahl der übertragenen Elektronen (auch Äquivalentzahl)
	Faraday-Konstante, F = 96485,34 C mol⁻¹ = 96485,34 J V⁻¹ mol⁻¹
	Aktivität des betreffenden Redox-Partners

Interpretation und Bedeutung

Galvanische Zelle

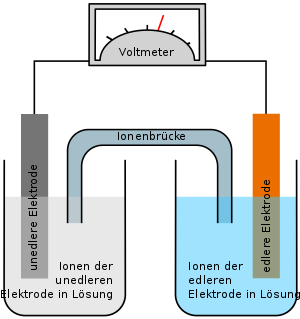
Jede Kombination von zwei Elektroden nennt man Galvanische Zelle (z. B. Batterien, Akkus oder auch biologische Zellen). Ihre Leerlaufspannung U₀ (historisch: Elektromotorische Kraft) ist gleich der Potentialdifferenz ΔE der Elektroden, die bei Anwendung der Nernst-Gleichung auf die Halbzellen als U₀ = ΔE = E_Akzeptor − E_Donator berechnet werden kann. Analog erlaubt sie die Berechnung der sich einstellenden Gleichgewichtsaktivitäten, wenn an die Halbzellen eine Spannung angelegt wird.

Die Nernst-Gleichung besitzt zentrale Bedeutung in der Elektrochemie, Galvanik und Elektroanalytik, weil sie die elektrische Größe Spannung (bzw. Elektrodenpotential) mit der chemischen Größe Konzentration verbindet. Sie ist streng genommen nur gültig für Zellen ohne Überführung und stromlose Vorgänge, bietet aber einen Ausgangspunkt für die Herleitung von Gleichungen in stromdurchflossenen elektrochemischen Systemen. Das Nernstpotential U₀ multipliziert mit der Ladung z·F für einen molaren Stoffumsatz z·F·U₀ ergibt die Gibbsenergie. ∆G = −z·F·U₀. Das Nernstpotential gibt demnach die chemische Energie der elektrochemischen Reaktion, geteilt durch die beteiligte Ladung an.

Alternative Formulierungen

Die Bezeichnung Nernst-Gleichung wird je nach Anwendung für verschiedene abgeleitete oder erweiterte Gleichungen benutzt.

Spezielle (historische) Nernst-Gleichung

Die ursprüngliche Form leitete im Jahr 1889 der deutsche Physiker und Chemiker Walther Nernst unter Verwendung von Konzentrationen c ab.

$E=E^{0}+{\frac {RT}{z_{\mathrm {e} }F}}\ln {\frac {c_{\mathrm {Ox} }}{c_{\mathrm {Red} }}}$

Der Faktor R T / z_e F wird Nernst-Faktor oder Elektrodensteilheit genannt; eine Wertetabelle für R T / z_e F bei verschiedenen Temperaturen befindet sich im Artikel zur Elektrodensteilheit.

Allgemeine Nernst-Gleichung (Herleitung)

Für die Änderung der Gibbs-Energie (Freien Enthalpie) $\Delta _{\mathrm {R} }G$ einer chemischen Reaktion, an der Stoffe $A_{1},\dots ,A_{k}$ gemäß

$\nu _{1}A_{1}+\nu _{2}A_{2}+\dots \longrightarrow \dots +\nu _{k-1}A_{k-1}+\nu _{k}A_{k}$

beteiligt sind, gilt

$\Delta _{\mathrm {R} }G=\Delta _{\mathrm {R} }G^{0}+RT\,\ln \prod _{i=1}^{k}a_{i}^{\nu _{i}}$

$a_{i}$	auf die Standardaktivität bezogene Aktivität des Stoffes
$\nu _{i}$	stöchiometrischer Koeffizient des Stoffes in der Reaktionsgleichung (negativ für Edukte)

Der Zusammenhang zwischen $\Delta _{\mathrm {R} }G$ und dem Logarithmus ist plausibel, da einerseits $\Delta _{\mathrm {R} }G$ proportional zur Teilchenzahl (oder der Schreibweise der chemischen Gleichung) ist, andererseits in den Aktivitätsquotienten die einzelnen Aktivitäten mit der Potenz der stöchiometrischen Koeffizienten eingehen. Der Logarithmus wandelt den Exponenten in einen Faktor um.

$\mathrm {2\,H_{2}+O_{2}\longrightarrow 2\,H_{2}O}$ ergibt pro $\mathrm {H_{2}O}$ dasselbe (elektro-)chemischen Potential wie $\mathrm {H_{2}+{1 \over 2}\ O_{2}\longrightarrow H_{2}O} \qquad$ .

$\Delta _{\mathrm {R} }G$ ist die bei konstantem Druck und konstanter Temperatur aus der Reaktion maximal gewinnbare Arbeit, die vollständig in nutzbare elektrische Arbeit umgewandelt werden kann. Aufgrund des Energieerhaltungssatzes gilt

$\Delta _{\mathrm {R} }G=-z_{e}\,F\,\Delta E$

was in der allgemeinen Nernst-Gleichung resultiert

$\Delta E=\Delta E^{0}-{\frac {RT}{z_{e}F}}\,\ln \prod _{i=1}^{k}a_{i}^{\nu _{i}}$

Die allgemeine Nernst-Gleichung erlaubt für die betrachtete Reaktion die Berechnung der Gleichgewichtskonstanten (für $\Delta E=0$ ), Richtung (freiwillig für $\Delta E>0$ , erzwungen für $\Delta E<0$ ) und Spannung $\Delta E$ , die die Reaktion liefert, wenn man ihre Redox-Teilreaktionen in getrennten Halbzellen ablaufen lässt.

siehe auch: chemisches Potential, elektrochemisches Potential.

Anwendung

Die Nernst-Gleichung findet in der potentiometrischen Titration Verwendung. Beispielsweise wird eine Messelektrode in eine Probelösung eingetaucht und muss auf das zu bestimmende Ion reagieren, das heißt, das Potential dieser Elektrode muss abhängig von der Konzentration des zu bestimmenden Ions sein. Diese Abhängigkeit wird durch die Nernst-Gleichung beschrieben. Bei dem Versuch ist darauf zu achten, dass die Messung stromlos erfolgt, da sich sonst durch Elektrolyse die Potentiale verfälschen würden. Man verwendete daher zur Messung eine Spannungs-Kompensationsschaltung.

Reduktion

Für die Reduktion

$\mathrm {Ox+{\mathit {z}}_{\mathit {e}}e^{-}\longrightarrow Red}$

geht die allgemeine Form unmittelbar in die erstgenannte Gleichung über. Diese Identität hat zwei praktische Bedeutungen:

Die elektrochemische Spannungsreihe listet prinzipiell Reduktionen.
Da man jede chemische Reaktion in Oxidations- und Reduktionsteilreaktionen von Redox-Paaren zerlegen kann, ist ΔE die Summe der mit den zugehörigen stöchiometrischen Koeffizienten multiplizierten Nernst-Gleichungen für die Teilreaktionen. Dabei gehen die Oxidationsteilreaktionen mit negativem stöchiometrischen Koeffizienten ein.

Knallgasreaktion

Die Teilreaktionen der so genannten Knallgasreaktion

$\mathrm{2 \ H_2 + O_2 \longrightarrow 2 \ H_2O}$

laufen als Oxidation

$\mathrm {2\ H_{2}\longrightarrow 4\ H^{+}+4\ e^{-}}$

bzw. Reduktion

$\mathrm {O_{2}+4\ e^{-}\longrightarrow 2\ O^{2-}}$

räumlich getrennt in Wasserstoff-Sauerstoff-Brennstoffzellen ab. Die damit erzielbare Spannung kann mit der Nernst-Gleichung berechnet werden und beträgt unter Standardbedingungen ΔE⁰ = 1,23 V.

Konzentrationselemente

Kupfer-Konzentrationselement

Ein Konzentrationselement besteht aus zwei Halbzellen, die Elektrolyte mit den gleichen Bestandteilen enthalten, aber mit unterschiedlicher Ionenkonzentration. Es eignet sich daher besonders zur Demonstration der Nernst-Gleichung.

Ein Beispiel ist ein Kupfer-Konzentrationselement aus zwei Kupferelektroden und zwei Kupfersulfatlösungen, die sich nur in der Konzentration unterscheiden. Bei Stromfluss gleichen sich dann die Konzentrationen in den Zellen an, denn es laufen dann folgende Reaktionen ab:

Die Reduktion in der Halbzelle mit der größeren Kupferionenkonzentration c_g:

$\mathrm {Cu^{2+}({\mathit {c}}_{g})+2\ e^{-}\longrightarrow Cu}$

Die Oxidation in der Halbzelle mit der kleineren Kupferionenkonzentration c_k:

$\mathrm {Cu\longrightarrow Cu^{2+}({\mathit {c}}_{k})+2\ e^{-}}$

Anhand der Nernst-Gleichungen für die Teilreaktionen oder mit der allgemeinen Nernst-Gleichung der Gesamtreaktion erhält man für die Spannung ΔE des Kupfer-Konzentrationselements:

$\Delta E={\frac {RT}{2F}}\ln {\frac {c_{\mathrm {g} }(\mathrm {Cu} ^{2+})}{c_{\mathrm {k} }(\mathrm {Cu} ^{2+})}}$

Allgemein gilt für die Spannung eines Konzentrationselements:

$\Delta E={\frac {RT}{z_{e}F}}\ln {\frac {a_{\mathrm {g} }}{a_{\mathrm {k} }}}$ .

Im Temperaturbereich von 22 bis 26 °C gilt:

$\Delta E={\frac {0{,}059V}{z_{e}}}\lg {\frac {a_{\mathrm {g} }}{a_{\mathrm {k} }}}$ .

Konzentrationselemente mit verschiedenen Elementen

Bei Konzentrationselementen mit unterschiedlichen Elementen und Konzentrationen, die von den Normalbedingungen abweichen, wird folgende Formel verwendet:

$E=E^{0}+{\frac {0{,}059V}{z_{e}}}\lg {\frac {(c_{\mathrm {ox} })^{a}}{(c_{\mathrm {red} })^{b}}}$ .

a = Vorfaktor der Oxidationsseite (Beispiel: 4 $H^{+}$ )
b = Vorfaktor der Reduktionsseite (Beispiel: 2 ${H_{2}}O$ )

pH-Wert

Betrachten wir H⁺-Konzentrations-Elemente ( $z_{e}=1$ ), dann geht die Nernst-Gleichung bei Raumtemperatur (T = 298,15 K ≙ 25 °C), Umwandlung des natürlichen Logarithmus in den dekadischen Logarithmus (lg a(H⁺) = ln a(H⁺) / ln 10) und unter Beachtung der Definition des pH-Wertes (pH = −lg a(H⁺)) in die Form

$\Delta E=-0{,}059\,\mathrm {V} \,(\mathrm {pH} _{1}-\mathrm {pH} _{2})$

über. Glaselektroden zur pH-Messung stellen im Prinzip solche H⁺-Konzentrations-Elemente dar. In ihnen befindet sich eine Lösung mit bekanntem pH-Wert. Wird Kontakt zu einer Lösung mit unbekanntem pH-Wert hergestellt, misst das zugehörige Messgerät eine Spannung, die mit dem Faktor 0,059 V direkt in einen pH-Wert umgerechnet und angezeigt wird. Der Faktor kann herstellungsbedingt variieren und muss vor der Verwendung kalibriert werden, liegt jedoch immer nahe 0,059 V.

Lambdasonden

Bei einer Lambdasonde, deren Sensorelement für Sauerstoffionen leitfähig ist, stellt sich aufgrund des Konzentrationsgefälles des Sauerstoffes zwischen Luft und Abgas eine Spannung ein, die benutzt wird, um mit der Lambdaregelung ein gewünschtes Gemisch einzustellen.

Nernst-Gleichung in der Biologie

In biologischen Systemen trennen Zellmembranen Bereiche unterschiedlicher Ionenkonzentrationen ab. Ist die Membran für ein bestimmtes Ion selektiv permeabel, wird es entlang des Konzentrationsgradienten diffundieren, gleichzeitig entsteht aber, da das Ion geladen ist, eine Spannung (Ruhemembranpotential). Mit der Nernst-Gleichung lässt sich die Gleichgewichtslage dieses Vorgangs beschreiben.

Gebräuchlich ist eine vereinfachte Form der Gleichung, bei der R, F und T (310 K) sowie der Umrechnungsfaktor zum dekadischen Logarithmus in eine Konstante gefasst werden:

$E={\frac {61{,}51\,\mathrm {mV} }{z_{e}}}\lg {\frac {c_{\mathrm {aussen} }}{c_{\mathrm {innen} }}}$

Siehe auch: Goldman-Gleichung

Siehe auch

Nernst-Planck-Gleichung

Basierend auf einem Artikel in:

Wikipedia.de