Elektromotorische Kraft

Die elektromotorische Kraft (EMK) (engl. Electromotive Force (EMF)) und – in gleicher Bedeutung – die Urspannung sind historisch gewachsene Bezeichnungen für die Quellenspannung einer elektrischen Spannungsquelle. Auch die in den Wicklungen eines Elektromotors oder Generators durch Drehung induzierte Spannung wird EMK genannt.

Man versteht darunter die Spannung eines Systems, die dieses theoretisch ohne eingespeisten oder gelieferten Strom und ohne Leckströme erzeugt bzw. erzeugen würde.

Der Begriff wird vor allem bei galvanischen Zellen oder für die Induktionsspannung bei elektrischen Maschinen verwendet. Der Begriff beschreibt trotz seiner Bezeichnung keine Kraft im physikalischen Sinn, sondern eine elektrische Spannung.

Geschichte

Der grundsätzliche Zusammenhang von chemisch geleisteter Arbeit in galvanischen Elementen zu Stromenergie, EMK und Kraft wurde durch Arbeiten von Hermann von Helmholtz und Josiah Willard Gibbs geleistet. Max Le Blanc nutzte zur Standardisierung der elektromotorischen Kraft von galvanischen Elementen die Normallösungen. Le Blanc fand weiter, dass platinierte Platinelektroden reversible Elektroden sind und zur präzisen Messung von Normalpotentialen genutzt werden können, er schlug die mit Wasserstoffgas umspülte Platinelektrode als Standardelektrode vor. Walther Nernst stellte eine Theorie zur EMK-Bestimmung bei verschiedenen Elektrolytkonzentrationen und Temperaturen auf.

Beispiele

Galvanische Zelle

Galvanische Zelle

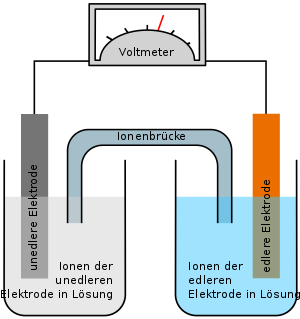
Das Daniell-Element ist ein historisches Beispiel für eine elektrochemische Zelle. Es wird aus einem Zinkstab gebildet, der in die wässrige Lösung eines Zinksalzes taucht und einem Kupferstab, der in die wässrige Lösung eines Kupfersalzes taucht. Beide Halbzellen werden mit Hilfe eines Stromschlüssels, der die Lösung eines Elektrolyten – KCl (Kaliumchlorid) oder NH₄NO₃ (Ammoniumnitrat) – enthält, oder durch ein Diaphragma zu einer galvanischen Zelle kombiniert.

Werden die beiden Metalle durch einen metallischen Leiter verbunden, fließt ein elektrischer Strom durch das System. Dabei erwärmt sich der Draht. Zink löst sich an der Zink-Elektrode auf, Kupferionen aus der Lösung scheiden sich an der Kupfer-Elektrode ab. Zur Bestimmung der EMK zerteilt man den Draht und schaltet ein Spannungsmessgerät zwischen die Drahtenden.

Im Daniell-Element findet an der Anode die Oxidation des Zinks statt.

${\mathrm {Zn\longrightarrow Zn^{{2+}}+2\ e^{-}}}$

An der Kathode wird Kupfer reduziert.

${\mathrm {Cu^{{2+}}+2\ e^{-}\longrightarrow Cu}}$

Für jede Halbzelle berechnen sich die Halbzellenpotentiale nach der Nernst-Gleichung.

$E=E_{0}+{\frac {RT}{z\cdot F}}\cdot \ln \left(a({\mathrm {Me}}^{{z+}})\right)$

	Potentialdifferenz bzw. elektrische Spannung gegen eine Referenzelektrode; [ $E\,$ ] = V
$E_{0}$	Standard-Potential (nachzuschlagen unter Spannungsreihe); [ $E_{0}$ ] = V
	Temperatur; [] = K
$a({\mathrm {Me}}^{{z+}})$	Aktivität der Metallionen in der Lösung
	Faraday-Konstante, = 96485,33 C/mol
	Universelle oder molare Gaskonstante, = 8,314460 J/mol K
	Anzahl der bei dem Potentialausgleich übertragenen Elektronen pro Atom oder Ion

Zur Berechnung der EMK für die Gesamtreaktion bildet man die Differenz der beiden Halbzellenpotentiale nach

$\Delta E=E_{\mathrm {Kathode} }-E_{\mathrm {Anode} }$

Für das Daniell-Element erhält man für Metallionenkonzentrationen von jeweils 1 mol/l

$\Delta E=E_{\mathrm {Kathode} }-E_{\mathrm {Anode} }=E_{\mathrm {Kupfer} }-E_{\mathrm {Zink} }=1{,}10\ \mathrm {V}$

da unter Standardbedingungen (Temperatur 25 °C, Konzentration 1 mol/l, Druck 1013 mbar) das Halbzellenpotential dem Standard-Potential entspricht.

Jede Halbzelle ist dabei getrennt zu betrachten. Man kann auch eine Halbzelle aus Zinkblech in Zinklösung nutzen, um auf elektrochemische Weise Wasserstoff herzustellen. Das Zinkblech wird mit einem Draht verbunden und in Kontakt mit einer Platinelektrode gebracht. Nun taucht man die Platinelektrode in Salzsäure. Es bildet sich Wasserstoffgas.

Zur Kalibrierung bzw. zur richtigen Einstellung von genau 1,000 V wurde in früherer Zeit das Clarkelement (Zink/Zinkpaste/Quecksilbersulfat/Quecksilber) oder das Westonelement benutzt.

Anwendungen

Aus der EMK lässt sich die molare freie Enthalpie einer Redox-Reaktion berechnen.

$\Delta G_{\mathrm {m} }=-z\cdot F\cdot \Delta E$

Hat man die EMK unter Standard-Bedingungen bestimmt, lässt sich so die freie Standard-Reaktionsenthalpie berechnen.

Weiterhin kann mit einer Referenz-Wasserstoffelektrode der pH-Wert bestimmt werden, indem die EMK dazu entwickelter Sonden gemessen wird, wenn sie in die zu messende Flüssigkeit eintauchen. Siehe hierzu zum Beispiel pH-Elektrode. Die EMK ändert sich dabei um 59,16 mV je pH-Änderung um 1, d.h. je Zehnerpotenz der Wasserstoff-Ionenkonzentration, wenn die Messtemperatur von 25 °C eingehalten wird (Nernst-Neigung). Andere Elektrodensysteme umgehen die schwierige Handhabung der Wasserstoffelektrode zur pH-Wert-Messung.

Elektromotoren und Generatoren

Bewegt sich ein elektrischer Leiter quer durch ein Magnetfeld, wird in ihm eine elektrische Spannung induziert; sie ist umso höher, je schneller die Bewegung ist. Dementsprechend induziert der sich im Stator-Magnetfeld drehende Läufer eines Elektromotors oder der magnetische Läufer eines Generators in seinen Wicklungen eine Spannung. Diese induzierte Spannung wird bei Motoren Gegen-EMK genannt. Dabei ist es unerheblich, welche Spannung tatsächlich am Motor bzw. Generator anliegt – die Differenz der beiden Spannungen fällt am Ohmschen Widerstand der Wicklungen ab oder wird durch Leckströme verursacht.

Steigt die Drehzahl eines Gleichstrommotors soweit an, dass die EMK sich der anliegenden Spannung nähert, sinkt die Stromaufnahme und die Drehzahl erhöht sich nicht weiter. Mit Kenntnis der Gegen-EMK eines Gleichstrommotors kann man somit dessen Grenzdrehzahl für eine bestimmte Spannung errechnen.

Die Gegen-EMK eines Gleichstrommotors und auch anderer Motoren kann zu deren Steuerung und Geschwindigkeitsregelung herangezogen werden. Davon wird zum Beispiel bei kleinen permanenterregten Motoren zum Antrieb von Kassetten-Tonbandgeräten Gebrauch gemacht, aber auch bei elektronisch kommutierten Motoren sowie bei modernen Frequenzumrichtern für Asynchronmotoren.

Fremderregte Gleichstrommotoren können durch Feldschwächung in ihrer Drehzahl erhöht werden – die Gegen-EMK erfordert nun eine höhere Drehzahl, um den Wert der Betriebsspannung zu erreichen.

Auch Asynchronmotoren induzieren eine Gegen-EMK – hier induziert das mit dem Kurzschlussläufer umlaufende Magnetfeld in den Statorwicklungen eine Wechselspannung, die der Stromaufnahme entgegenwirkt, wenn der Läufer die Nenndrehzahl erreicht hat.

Die EMK von Schrittmotoren begrenzt deren Dynamik bzw. das Drehmoment bei großen Drehzahlen.

Die elektromotorische Kraft ist bei Generatoren nahezu gleich der Leerlaufspannung. Die erzeugte Spannung beziehungsweise die EMK von Generatoren kann durch Verändern der Drehzahl oder des Erregerfeldes verändert werden.

Galvanometer-Antriebe und Lautsprecher

Bei Galvanometer-Antrieben und elektrodynamischen Lautsprechern spielt die Gegen-EMK ebenfalls eine Rolle: sie wirken durch die Massenträgheit ihrer Spulen auf die speisende Spannungsquelle zurück. Ihre EMK wird in der Regel durch den geringen Innenwiderstand der sie treibenden Spannungsquellen kurzgeschlossen, dadurch werden sie bedämpft – ein Nachschwingen oder Überschwinger werden verringert.

Feldtheoretische Einordnung

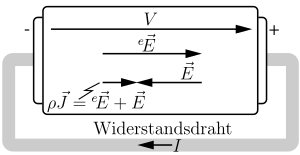
Elektrochemische Zelle im Entladebetrieb

Die stromtreibende elektromotorische Kraft (EMK, eingepräge Spannung, Urspannung) ist nach ihrer Entstehung nichtelektrischer Natur (z.B. in elektrochemischen Zellen, in Photozellen, in Thermoelementen, bei Diffusionsvorgängen, in magnetfeldbasierten elektrischen Generatoren oder Motoren). Sie kann formal auf eine eingeprägte (innere, nichtelektrische) Feldstärke $^{e}\!{\vec {E}}$ zurückgeführt werden, die nur innerhalb der Quelle existiert. $^{e}\!{\vec {E}}$ ist unabhängig von der Belastung der Quelle, so dass auch die EMK

$V=\int _{\mathcal {S}}{}^{e}\!{\vec {E}}\mathrm {d} {\vec {s}}$

wie die Quellenspannung $U_{Q}$ unabhängig von der Belastung ist. Der Integrationsweg $\mathcal{S}$ verläuft ganz innerhalb der Quelle von einem Pol zum anderen. ergibt sich positiv, wenn der Weg vom Minus- zum Pluspol führt ( ${\mathcal {S}}={\mathcal {S}}_{-+}$ ).

Im Gebiet elektromotorischer Kräfte gilt das erweiterte Ohmsche Gesetz ${\vec {J}}=({}^{e}\!{\vec {E}}+{\vec {E}})/\rho$ . Die eine Ladung verschiebende Kraft ist dort gleich $q(^{e}\!{\vec {E}}+{\vec {E}})$ . In der Akkumulatorzelle rechts, dargestellt ist der Entladefall, kompensieren sich im Leerlauf ( ${\vec {J}}=0$ ) die eingeprägte elektrische Feldstärke $^{e}\!{\vec {E}}$ und die von den Polladungen erregte elektrische Feldstärke ${\vec {E}}$ gemäß ${\vec {E}}=-^{e}\!{\vec {E}}$ , so dass keine Ladung in der Zelle transportiert wird. Die EMK

$V=\int _{{\mathcal {S}}_{-+}}\!\!\!\!{}^{e}\!{\vec {E}}\mathrm {d} {\vec {s}}=\int _{{\mathcal {S}}_{-+}}\!\!\!\!-{\vec {E}}\mathrm {d} {\vec {s}}=-U_{Q}$

ist dann an den Anschlüssen als Quellenspannung messbar.

In der zusammenfassenden Gleichungskette für die rechts skizzierte elektrochemische Zelle

$I{\stackrel {\circ }{R}}=I\oint {\frac {\rho }{A}}\mathrm {d} s=\oint \rho {\vec {J}}\mathrm {d} {\vec {s}}=\oint ({}^{e}\!{\vec {E}}+{\vec {E}})\mathrm {d} {\vec {s}}=\oint {}^{e}\!{\vec {E}}\mathrm {d} {\vec {s}}=V$

bedeutet ${\stackrel {\circ }{R}}$ den Umlaufwiderstand des Stromkreises, also die Summe aus Innen- und Außenwiderstand, den ortsabhängigen Querschnittsflächeninhalt und $\rho$ den ortsabhängigen spezifischen elektrischen Widerstand. Der Umlaufsinn der Integrale ist wie der Weg vom Minus- zum Pluspol in der Quelle orientiert.

Wenn sich der Leiterkreis in einem Magnetfeld bewegt ( ${\vec {v}}\neq 0$ , z.B. in elektrischen Maschinen), ist die Feldstärke ${\vec {v}}\times {\vec {B}}$ der Lorentzkraft als eingeprägte elektrische Feldstärke $^{e}\!{\vec {E}}$ zu rechnen. Der Leiterkreis wird dadurch insgesamt zur Quelle. Wenn das Magnetfeld zeitveränderlich ist ( $\partial {\vec {B}}/\partial t\neq 0$ ), ist die Zirkulation der elektrischen Feldstärke nicht mehr gleich null, wie in der Gleichungskette oben vorausgesetzt. Es gilt vielmehr

$\oint {\vec {E}}\cdot \mathrm {d} {\vec {s}}=-\int {\frac {\partial {\vec {B}}}{\partial t}}\mathrm {d} {\vec {A}}$

nach dem Induktionsgesetz. Die induzierte Spannung

$U_{i}=-\int \limits _{{\mathcal {A}}(t)}{\frac {\partial {\vec {B}}}{\partial t}}{\text{d}}{\vec {A}}+\oint _{\partial {\mathcal {A}}(t)}{\vec {v}}\times {\vec {B}}\ {\text{d}}{\vec {s}}$

bildet einen Teil der elektromotorischen Kraft.

Wenn man die stromtreibende Wirkung der Quellen nicht durch ihre Quellenspannung, sondern durch ihre EMK berücksichtigt, nimmt der Kirchhoffsche Maschensatz statt $\sum U=0$ die Form $\sum V=\sum U$ an. Die anschaulichere Form mit , die „Motor“ und „Fahrwerk“ unterscheidet, ist weniger üblich.

Die Aussage, EMK sei eine veraltete Bezeichnung für Quellenspannung, suggeriert, es handele sich um Synonyme für dieselbe physikalische Größe. Das ist nur soweit richtig, als EMK und Quellenspannung betragsgleich sind. Ihre Richtungen sind entgegengesetzt und ihre Definitionen fußen, wie oben dargestellt, auf verschiedenen Feldgrößen. In einer hydraulischen Analogie entspricht die EMK der Druckerzeugung einer Pumpe und die Quellenspannung dem (vermeintlichen) Druckabfall, den man an der Pumpe von der Druck- zur Saugseite misst.

Die EMK treibt einen elektrischen Strom in ihrer Richtung an, die Quellenspannung entgegen ihrer Richtung.

Literatur

Paul B. Arthur Linker: Elektrotechnische Meßkunde. 3., völlig umgearbeitete und erweiterte Auflage. Julius Springer, Berlin 1920.
Max Le Blanc: Lehrbuch der Elektrochemie. 9. und 10. Auflage. Oskar Leiner, Leipzig 1922

Basierend auf einem Artikel in:

Wikipedia.de