Sinusspannung

Viele Wechselspannungen wie die Netzspannung im öffentlichen Energieversorgungsnetz haben einen sinusförmigen Spannungsverlauf und können dann als Sinusspannung bezeichnet werden.

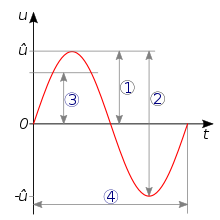
Eine sinusförmige Wechselspannung
1 = Scheitelwert
2 = Spitze-Tal-Wert
3 = Effektivwert
4 = Periodendauer

Der charakteristische Sinusverlauf ergibt sich durch die Drehbewegung, mit der im Wechselstromgenerator eine Leiterschleife mit konstanter Winkelgeschwindigkeit im Magnetfeld bewegt wird und dabei eine Spannung induziert wird.

Drei verkettete (zeitlich versetzte und auf drei Leiter verteilte) Wechselströme bilden ein System, das als Dreiphasenwechselstrom (Drehstrom) bezeichnet wird.

Zeitlicher Verlauf

Für die zeitliche Abhängigkeit einer Sinusspannung mit Amplitude $\hat u$ und Frequenz bzw. Kreisfrequenz $\omega$ bzw. Periodendauer gilt:

$u(t)={\hat u}\,\sin(\omega t)={\hat u}\,\sin(2\pi ft)={\hat u}\,\sin {\frac {2\pi t}T}$ mit $f={\frac {1}{T}}$ .

Verlauf der Sinusspannung mit Skalenbeschriftung auf der Zeit- bzw. Winkelachse

Im öffentlichen Netz beträgt $f={\text{ 50 Hz}}$ und somit $T={\frac {1}{f}}={\text{0,02 s = 20 ms}}$ .

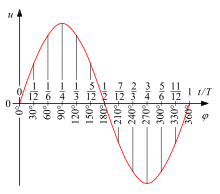
Die momentane Spannung lässt sich auch in Abhängigkeit vom Phasenwinkel $\varphi (t)=\omega t$ angeben durch:

$u={\hat u}\cdot \sin(\varphi )\,,$

wobei bei dieser Darstellung 0° als Anfang einer Periode in einen Nulldurchgang mit positivem Anstieg gelegt wird und 360° als Ende der Periode in den nächsten Nulldurchgang mit wieder positivem Anstieg.

Für spezielle Winkel gibt es eine einfache Merkregel:

φ	sin φ	dezimal
0°	${\tfrac 12}{\sqrt 0}$	0,000
30°	${\tfrac 12}{\sqrt 1}$	0,500
45°	${\tfrac 12}{\sqrt 2}$	0,707
60°	${\tfrac 12}{\sqrt 3}$	0,866
90°	${\tfrac 12}{\sqrt 4}$	1,000

Auch mit der Kosinusfunktion beschriebene Wechselspannungen heißen sinusförmig.

Effektivwert

Der Effektivwert einer Spannung wird mit $U_{\mathrm {eff} }$ bezeichnet, in der Elektrotechnik auch kurz mit . Der Effektivwert einer Wechselspannung ist so groß wie die Gleichspannung, mit der an einem ohmschen Verbraucher (z.B. Heizung) dieselbe Leistung umgesetzt wird wie mit der Wechselspannung. Bei Angaben zu Wechselspannungen wird meistens der Effektivwert angegeben (so z.B. bei einer 230-V-Netzspannung.) Dieser Wert von Sinus-Wechselspannungen lässt sich aus der Amplitude berechnen, wie das unter Effektivwert angegeben ist:

$U_{\mathrm {eff} }=U={\sqrt {{\frac {1}{T}}\int _{0}^{T}({\hat {u}}\sin(2\pi ft))^{2}\mathrm {d} t}}={\frac {\hat {u}}{\sqrt {2}}}$

und umgekehrt aus dem Effektivwert der Scheitelwert:

${{\hat u}}={U_{{\mathrm {eff}}}}\cdot {{\sqrt 2}}\,.$

Das Verhältnis Scheitelwert zu Effektivwert wird als Scheitelfaktor bezeichnet, der bei Sinus-Wechselspannungen den Wert ${\sqrt {2}}$ annimmt.

Basierend auf einem Artikel in:

Wikipedia.de