
Scheitelfaktor
Der Scheitelfaktor oder Crest-Faktor (englisch crest factor) beschreibt in der Elektrotechnik das Verhältnis von Scheitelwert zu Effektivwert einer Wechselgröße und ist immer größer oder gleich eins. Anwendung findet er in Bereichen der elektrischen Messtechnik, Nachrichtentechnik, Tontechnik und Akustik.
Er dient wie der Formfaktor oder der Klirrfaktor als Kennwert zur groben Beschreibung der Kurvenform einer Wechselgröße.
Das Quadrat des Scheitelfaktors wird als englisch Peak-to-average power ratio (PAPR) bezeichnet und drückt das Verhältnis von Spitzenleistung zu der mittleren Leistung eines Signals aus. Der PAPR wird üblicherweise als logarithmisches Maß in Dezibel angegeben. Er dient unter anderem bei Funkempfängern zur Gewinnung eines Steuersignals zur automatischen Verstärkungsregelung (AGC).
Definition
Der Scheitelfaktor der Größe
ist definiert als:
Beispiel: Wenn eine sinusförmige Wechselspannung einen Effektivwert von
230 V
aufweist, beträgt der Spitzenwert ca. 325 V. Der Scheitelfaktor
ist in diesem Fall
.
Praktische Bedeutung
Messgeräte für Wechselstrom und -spannung mit Effektivwertmessung müssen Momentanwerte um den Spitzenwert des Messsignales herum ausreichend schnell verarbeiten können. Einfache elektronische Stromzähler und Strommessgeräte arbeiten bei hohen Scheitelfaktoren daher oft ungenau, da sie entweder einen zu geringen Dynamikumfang haben und/oder eine zu geringe Abtastrate.
Hohe Scheitelfaktoren des aufgenommenen Stromes von netzbetriebenen Geräten bedeuten einen hohen Anteil von Oberschwingungen im Stromnetz, es entstehen aufgrund des Innenwiderstandes des Stromnetzes daraus auch Verzerrungen der Sinusform der Spannung. Verbraucher mit hohen Crestfaktoren bei der Stromaufnahme verursachen eine hohe Verzerrungsblindleistung. Typische Beispiele sind Schaltnetzteile, Stromrichter und Frequenzumrichter ohne Leistungsfaktorkorrektur. Der Effektivstrom ist höher als der für die aufgenommene Leistung zu erwartende Strom. Der Nullleiter im Drehstromnetz kann trotz symmetrischer Belastung mit einphasigen Verbrauchern mit verzerrter Stromaufnahme einen stark erhöhten Strom führen, der ihn überlastet, obwohl in den Außenleitern kein Überstrom herrscht. Hohe Scheitelfaktoren sind daher unerwünscht. Sie werden durch die Leistungsfaktorkorrektur vermieden.
Auch Netztransformatoren werden durch angeschlossene Gleichrichter und Siebkondensatoren weit höher belastet als bei einer ohmschen Last, da der Strom zum Nachladen des Kondensators nur während des Stromflusswinkels fließt.
Thyristorsteller und Dimmer haben bei Teillastbetrieb eine stark verzerrte, impulsförmige Stromaufnahme. Der von ihnen aufgenommene Strom hat teilweise einen sehr hohen Scheitelfaktor von bis über 10.
In der Akustik bzw. Tontechnik sind hohe Crestfaktoren des Signales als auch der Hüllkurve typisch und bestimmen die erforderliche Aussteuerbarkeit von Verstärkern, Lautsprechern, Mikrofonen und Tonträgern. Aussteuerungsanzeigen berücksichtigen das durch das sogenannte True Peak Meter, das es dem Tonmeister ermöglicht, die Aussteuerung zurückzunehmen, um Verzerrungen vorzubeugen. Gute Tontechnik muss hohe Crestfaktoren verarbeiten können, ohne zu übersteuern. Dynamikkompression kann das zwar ebenfalls vermeiden, führt jedoch zu einem Informationsverlust bzw. zu verminderter Musikqualität.
PAPR
Das Verhältnis von Spitzenleistung zu der mittleren Leistung eines Signals, englisch Peak-to-Average Power Ratio und abgekürzt PAPR, ist:
Logarithmisch ausgedrückt ist dies:
Scheitelfaktor-Werte (Beispiele)
Folgende Tabelle zeigt die Scheitelfaktoren und PAPR für verschiedene, einfache Signalformen und einige in der Nachrichtentechnik übliche Modulationsverfahren. Bei den angeführten Modulationsverfahren (modulierte HF-Signale) bezieht man den Crestfaktor auf das leistungsstärkste Symbol. Ein frequenzmoduliertes Signal beispielsweise besitzt eine konstante Hüllkurve und damit einen Crestfaktor von 1.
| Schwingungsart | Schwingungsform | Betragsmittel durch Scheitelwert |
Formfaktor
= Betragsmittel durch Effektivwert |
Scheitelfaktor = Scheitelwert durch Effektivwert |
PAPR |
|---|---|---|---|---|---|
| Sinusschwingung | 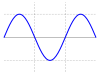 |
||||
| Volle Schwingung gleichgerichteter Sinus |
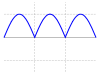 |
||||
| Halbschwingung gleichgerichteter Sinus |
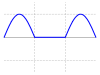 |
||||
| Dreiecksschwingung | 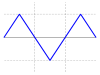 |
||||
| Symmetrische Rechteckschwingung |
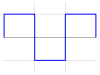 |
||||
| Unsymmetrische Rechteckschwingung (PWM-Signal) |
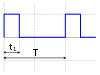 |
||||
| Frequenz- oder Phasenmodulation, z.B. GMSK bzw. QPSK |
|||||
| 4-Bit-Quadratur-Amplituden- modulation (16-QAM) |
|||||
| 6-Bit-Quadratur-Amplituden- modulation (64-QAM) |
Literatur
- Rene Flosdorff, Günther Hilgarth: Elektrische Energieverteilung. Teubner, 2003, ISBN 3-519-26424-2.
- Jürgen Nitsch, Uwe Knauff, Mathias Magdowski: Einführung in die Elektrotechnik. 2. Auflage. Shaker, 2011, ISBN 978-3-8322-7684-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.11. 2025