Erster Hauptsatz der Thermodynamik

Der Erste Hauptsatz der Thermodynamik beschreibt die Energieerhaltung in thermodynamischen Systemen. Er sagt aus, dass die Energie eines abgeschlossenen Systems konstant ist. Ausgehend von dieser Aussage lässt sich die Energiebilanz bilden: In einem geschlossenen System ist die Summe der inneren und äußeren Energie die Summe der am System verrichteten oder dem System entnommenen Arbeit und Wärme. Im offenen System müssen zusätzlich Volumenarbeit und mit Massenströmen zu- oder abgeführte Energien betrachtet werden. Bei stationären Prozessen und Kreisprozessen wird die Energiebilanz vereinfacht, da es keine zeitliche Änderung der Zustandsgrößen gibt.

Energiebilanz für das geschlossene System

Der erste Hauptsatz der Thermodynamik ist aus dem Satz der Energieerhaltung abgeleitet: Jedes System besitzt eine innere Energie , eine extensive Zustandsgröße. Diese kann sich nur durch den Transport von Energie in Form von Arbeit und/oder Wärme über die Grenze des Systems ändern. Es gilt:

$\qquad \mathrm {d} U=\delta Q+\delta W$

Dabei ist die Summe aus der Volumenarbeit und der im System dissipierten Arbeit (z. B. Reibungsarbeit), $\delta$ kennzeichnet unvollständige Differentiale, während $\mathrm {d}$ vollständige Differentiale kennzeichnet.

Die Gleichung gilt für das ruhende System. Beim bewegten System kommen die äußeren Energien $E_{a}$ (potentielle und kinetische Energie) hinzu:

$\qquad \mathrm {d} U+dE_{a}=\delta Q+\delta W$

Die Energie eines abgeschlossenen Systems bleibt unverändert. Verschiedene Energieformen können sich demnach ineinander umwandeln, aber Energie kann weder aus dem Nichts erzeugt noch kann sie vernichtet werden. Deshalb ist ein Perpetuum Mobile erster Art unmöglich (kein System verrichtet Arbeit ohne Zufuhr einer anderen Energieform und/oder ohne Verringerung seiner inneren Energie).

Eine Einschränkung der Umwandelbarkeit von Wärme in Arbeit ergibt sich erst aus dem zweiten Hauptsatz der Thermodynamik.

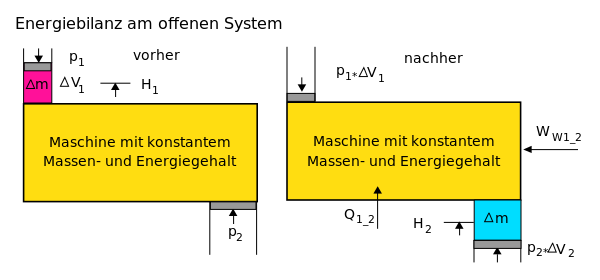
Energiebilanz für ein beliebiges offenes System

Auf das offene System angewendet, wird der erste Hauptsatz mathematisch anders formuliert. Beim offenen System fließen über die bestimmte Systemgrenze zusätzlich zur mechanischen Arbeit an der verschiebbaren Systemgrenze (Volumenänderungsarbeit z.B. am Kolben in einem Zylinder) die Verschiebearbeiten der Massenströme am Ein- und Austritt. Sie sind das Produkt aus Druck und Volumen. Statt mit der inneren Energie wird beim offenen System deshalb mit den Enthalpien bilanziert, die diesen Term enthalten. Es ist: $H=U+p\cdot V$ bzw. $h=u+p\cdot v$

Die Bilanzgleichung für ein instationäres System, bei dem sowohl Masseinhalt als auch Energieinhalt sich zeitlich ändern, lautet:

${\frac {dE_{\mathrm {sys} }}{dt}}=\sum _{i}^{\ }{\dot {Q}}_{i}+\sum _{j}^{\ }{\dot {W}}_{t,j}+\sum _{e}^{\ }{\dot {m}}_{e}\cdot \left(h_{e}+g\cdot z_{e}+{\frac {1}{2}}c_{e}^{2}\right)-\sum _{a}^{\ }{\dot {m}}_{a}\cdot \left(h_{a}+g\cdot z_{a}+{\frac {1}{2}}c_{a}^{2}\right)$

Dabei ist:

$\qquad {dE_{\mathrm {sys} } \over dt}$ die zeitliche Änderung der inneren Energie des Systems.

$\qquad {\dot {Q_{\mathrm {i} }}}$ der Wärmestrom über die Systemgrenze.

$\qquad {\dot {W_{\mathrm {t,j} }}}$ der Arbeitsstrom (technische Arbeit) über die Systemgrenze.

$\qquad {\dot {m_{\mathrm {e} }}}$ der Massenstrom in das System.

$\qquad {\dot {m_{\mathrm {a} }}}$ der Massenstrom aus dem System.

$\qquad h$ die spezifische Enthalpie.

$\qquad g\cdot z$ die spezifische potentielle Energie (mit $\qquad z$ = Höhe über dem Bezugsniveau und $\qquad g$ = Erdbeschleunigung).

$\qquad {1 \over 2}c^{2}$ die spezifische kinetische Energie (mit $\qquad c$ = Geschwindigkeit).

Sonderfälle und Vereinfachungen

Energiebilanz am offenen stationären System. Es wird ein kleiner Zeitraum $\Delta t$ betrachtet, in dem die Masse $\Delta m$ mit dem Zustand 1 in das System fließt und dieses im Zustand 2 wieder verlässt. Der Massenstrom ist dann $\Delta m$ / $\Delta t$ . Die Verschiebarbeiten am Eintritt und Austritt werden jeweils mit der inneren Energie in der Enthalpie zusammengefasst.

Geschlossenes System: ${\dot {m_{\mathrm {e} }}}={\dot {m_{\mathrm {a} }}}=0$ (siehe oben)
Stationärer Prozess : ${\dot {m_{\mathrm {e} }}}={\dot {m_{\mathrm {a} }}}={\dot {m}}$ und ${\textstyle {dE_{\mathrm {sys} } \over dt}=0}$ (siehe nebenstehendes Bild)

${\dot {Q}}+{\dot {W_{t}}}+{\dot {m}}\cdot \left(h_{\mathrm {e} }-h_{\mathrm {a} }+g\cdot z_{\mathrm {e} }-g\cdot z_{\mathrm {a} }+{1 \over 2}c_{\mathrm {e} }^{2}-{1 \over 2}c_{\mathrm {a} }^{2}\right)=0$

oder:

$\mathrm {\dot {Q}} +{\dot {W}}_{t}={\dot {m}}\cdot \left(h_{a}-h_{e}+\Delta e_{a}\right)$

zusätzlich adiabat (z.B. Dampfturbine): ${\dot {Q}}=0$

$P={\dot {m}}\cdot {\left(h_{a}-h_{e}+\Delta e_{a}\right)}$

Dabei ist P die Wellenleistung der Maschine. Da vom System abgegebene Energien in der Thermodynamik negativ definiert sind, wird die Leistung einer Turbine aus dieser Gleichung negativ. In der Praxis wird das Vorzeichen deshalb gewechselt. In vereinfachten Berechnungen vernachlässigt man auch die äußeren Energien. Dann lässt sich bei bekannten Zuständen am Eintritt und Austritt die spezifische Leistung direkt als Ordinatendifferenz aus dem h-s-Diagramm ablesen.

Energiebilanz für Kreisprozesse

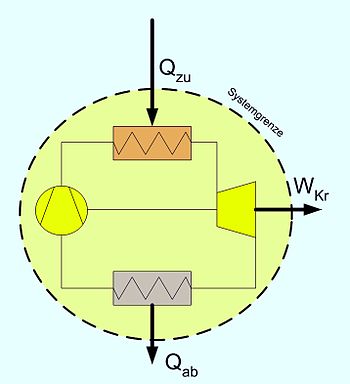
1. Hauptsatz für den Kreisprozess. Ein Kreisprozess kann als geschlossenes, inhomogenes System betrachtet werden, über dessen Grenze nur Wärme und Arbeit fließt. Als Beispiel ist hier ein Gasturbinenprozess mit Wärmeübertragern gezeichnet.

Da nach dem Durchlaufen eines Kreisprozesses das Arbeitsmedium zum Ausgangszustand zurückkehrt, vereinfacht sich die Bilanz. Es entfallen die zeitlichen Änderungen der Zustandsgrößen und es verbleiben die Prozessgrößen Wärme und Arbeit. Gemäß dem Zweiten Hauptsatz der Thermodynamik kann nicht nur Wärme zugeführt werden, die komplett in Arbeit umgewandelt wird, sondern es muss auch Wärme abgeführt werden. Die einfache Bilanzgleichung lautet:

$W_{\mathrm {Kr} }=-\oint \delta Q$

Dabei summiert das Kreisintegral alle Wärmeströme auf. Sie sind positiv, wenn sie in das System eintreten und negativ, wenn sie es verlassen. $W_{\mathrm {Kr} }$ ist die gesamte Arbeit des Zyklus. Sie ist negativ, wenn sie abgegeben wird.

Die Beziehung wird auch oft mit den Wärmebeträgen geschrieben:

$W_{\mathrm {Kr} }=Q_{\mathrm {zu} }-\left|Q_{\mathrm {ab} }\right|$ ,

wobei die Wärmeabfuhr deutlicher erkennbar wird.

Schließlich sollte auch der thermische Wirkungsgrad einer Kraftmaschine

$\eta _{\mathrm {th} }={\frac {{Q_{\mathrm {zu} }}-\left|Q_{\mathrm {ab} }\right|}{Q_{\mathrm {zu} }}}$

noch genannt werden, der den Nutzen (die Kreisprozessarbeit) ins Verhältnis zum Aufwand setzt (die zugeführte Wärme, die meist in Form von Brennstoff erzeugt werden muss). Die abgeführte Wärme wird bei technischen Realisierungen in der Regel von der Umgebung aufgenommen.

Siehe auch

Nernst-Theorem (Dritter Hauptsatz der Thermodynamik)

Literatur

Karl Stephan, Franz Mayinger: Thermodynamik. Grundlagen und technische Anwendungen. 2 Bände, Springer Verlag
- Band 1: Einstoffsysteme. 15. Auflage, 1998, ISBN 3-540-64250-1.
- Band 2: Mehrstoffsysteme und chemische Reaktionen. 14. Auflage, 1999, ISBN 3-540-64481-4.

Basierend auf einem Artikel in:

Wikipedia.de