Dichteanomalie

Wegen der Dichteanomalie beim Erstarren von Wasser schwimmt Eis oben.

Bei den meisten Stoffen nimmt die Dichte mit abnehmender Temperatur zu, auch über eine Aggregatzustandsänderung hinweg. Ein chemischer Stoff zeigt eine Dichteanomalie, wenn sich seine Dichte unterhalb einer bestimmten Temperatur bei Temperaturabnahme verringert, der Stoff sich also bei Abkühlung ausdehnt (negative thermische Ausdehnung).

Dichteanomalien treten bei den chemischen Elementen Antimon, Bismut, Gallium, Germanium, geschmolzenem Lithium, Plutonium, Silicium und Tellur auf, ebenfalls bei Legierungen wie Woodsches Metall und Verbindungen wie Zirkoniumwolframat ( ${\ce {ZrW2O8}}$ ), ${\ce {ZrV2O7}}$ , ${\ce {HfV2O7}}$ oder Zinkcyanid. Wasser ist der wichtigste Stoff, bei dem eine solche Anomalie auftritt: Hier wird zum einen die maximale Dichte des flüssigen Wassers oberhalb von 0 °C erreicht, zum anderen besitzt Eis eine geringere Dichte als flüssiges Wasser.

Auch manche stark polaren Flüssiggase zeigen Dichteanomalien, z.B. Fluorwasserstoff und Ammoniak. Auch bei der Umwandlung von β-Zinn unterhalb 13,2 °C in eine andere Modifikation (α-Zinn) ändert sich dessen Dichte, hier aber unumkehrbar.

Anwendung

Stoffe mit Dichteanomalie können ihre ingenieurwissenschaftliche Anwendung als Kompensator thermischer Ausdehnung finden. Dabei bringt man Stoffe mit positiver thermischer Ausdehnung und Stoffe mit negativer thermischer Ausdehnung (also mit Dichteanomalie) zusammen, sodass sich bei einer Temperaturveränderung Ausdehnung und Kontraktion ausgleichen und das Material sein Volumen gar nicht oder genau definiert mit Temperatur verändert. Eine thermische Ausdehnung nahe Null garantiert unveränderte Performance bei verschiedenen Temperaturen.

Ein gutes Beispiel aus dem Alltag für Materialien mit einer thermischen Ausdehnung nahe null sind Glaskeramik-Kochfelder wie z.B. Ceran. Diese weisen eine hohe Temperaturwechselbeständigkeit auf, sodass das Glas nicht springt, wenn es auf einer Seite erhitzt wird, während die andere Seite Raumtemperatur aufweist. Das liegt darin, dass manche in diesen Keramiken enthaltenen Phasen eine Dichteanomalie besitzen. Die Glaskeramik wird mit Hilfe der chemischen Zusammensetzung so eingestellt, dass die negative thermische Ausdehnung dieser Phasen bei einer Temperaturveränderung die positive thermische Ausdehnung anderer Phasen kompensiert. Dann weist das gesamte Kochfeld kaum thermische Ausdehnung auf und das Ceran springt nicht, wenn es nicht gleichmäßig überall erwärmt wird.

Gerade im Ingenieurwesen z.B. bei der Herstellung von Präzisionsinstrumenten ist man immer auf der Suche nach Materialien mit möglichst konstanter Performance in verschiedenen Temperaturbereichen. Dabei eignen sich dann gerade Materialien mit Dichteanomalie und kubischem Gitter, da diese isotrope negative thermische Ausdehnung aufweisen, d.h., dass ihre Ausdehnung in alle drei Raumrichtungen gleich ist. Beispiele dafür sind unter anderem ${\ce {ZrW2O8}}$ , ${\ce {ZrV2O7}}$ und ${\ce {HfV2O7}}$ . Während ${\ce {ZrW2O8}}$ über einen Temperaturbereich von 0,3 bis 1050 K negative thermische Ausdehnung besitzt, zeigt sich bei ${\ce {ZrV2O7}}$ und ${\ce {HfV2O7}}$ die Dichteanomalie allerdings nur in ihrer Hochtemperaturphase beginnend bei 350 bis 400 K.

Es kann allerdings auch nützlich sein, Materialien mit einer genau definierten thermischen Ausdehnung zu designen. Bei Zahnimplantaten ist es wichtig, dass sich die Füllung nicht deutlich stärker oder schwächer mit Temperatur ausdehnt, wenn man z.B. ein heißes oder kaltes Getränk zu sich nimmt. Daher kann es von Vorteil sein, die Gesamtausdehnung des Implantats durch die Verwendung von Materialien mit positiver und negativer thermischer Ausdehnung auf die Ausdehnung der Zähne abzustimmen.

Beispiele

Wasser

Dichte von Eis und Wasser in Abhängigkeit von der Temperatur, bei Normaldruck

Bei Normaldruck hat Wasser seine größte Dichte von ca. 1000 Kilogramm pro Kubikmeter bei 3,98 °C und ist flüssig. Unterhalb von 3,98 °C dehnt sich Wasser bei (weiterer) Temperaturverringerung – auch beim Wechsel zum festen Aggregatzustand – (wieder) aus. Die Anomalie des Wassers besteht also im Bereich zwischen 0 °C und 3,98 °C, das Eis verhält sich nicht anomal, wenn auch untypischerweise die Dichte des Eises geringer ist als die des flüssigen Wassers. Die derzeit genauesten publizierten Werte für die maximale Dichte liegen bei (999,974950 ± 0,00084) kg/m³ bei einer Temperatur von (3,983 ± 0,00067) °C. Die Werte stellen einen Mittelwert der von verschiedenen physikalischen Instituten veröffentlichten Zahlen dar (Stand 2005).

Die Berechnung der Dichte von luftfreiem Wasser D_LF in Abhängigkeit von der Temperatur T ([T] = °C) kann mit Hilfe der folgenden Virialgleichung erfolgen:

${\frac {D_{{{\rm {LF}}}}}{{\rm {g/l}}}}={\frac {a_{0}+a_{1}T+a_{2}T^{2}+a_{3}T^{3}+a_{4}T^{4}+a_{5}T^{5}}{1+bT}}$ .

mit den Koeffizienten: a₀ = 999,83952; a₁ = 16,952577 (°C)⁻¹; a₂ = −7,9905127·10⁻³ (°C)⁻²; a₃ = −4,6241757·10⁻⁵ (°C)⁻³; a₄ = 1,0584601·10⁻⁷ (°C)⁻⁴; a₅ = −2,8103006·10⁻¹⁰ (°C)⁻⁵ und b = 0,0168872. Für die Berechnung der Dichte von luftgesättigtem Wasser korrigiert man den Wert nach D_LG/(g/l) = D_LF/(g/l) − 0,004612 + 0,000106 (°C)⁻¹·T.

Im festen Aggregatzustand – in diesem Fall bei Eis – wird normalerweise eine hohe Fernordnung durch Ausbildung eines Kristallgitters im Zuge der Kristallisation erreicht. Im flüssigen Zustand herrscht eine Mischung von Ordnung und Chaos, wobei die Moleküle aufgrund ihrer höheren Geschwindigkeit ein größeres Volumen ausfüllen. Es erhöht sich also das Volumen, die Dichte wird damit geringer. Im gasförmigen Zustand ist die maximale Unordnung erreicht, d.h. die Moleküle verteilen sich dementsprechend gleichmäßig über den maximal zur Verfügung stehenden Raum.

Temperaturverteilung in einem stehenden See im Sommer und Winter

Der Grund der Anomalie des Wassers liegt in der Verkettung der Wassermoleküle über Wasserstoffbrückenbindungen. Durch sie benötigt die Struktur im festen Zustand mehr Raum als bei beweglichen Molekülen. Die Strukturbildung ist ein fortschreitender Vorgang, das heißt, es sind schon im flüssigen Zustand so genannte Cluster aus Wassermolekülen vorhanden. Bei 3,98 °C ist der Zustand erreicht, bei dem die einzelnen Cluster das geringste Volumen einnehmen und damit die größte Dichte haben. Wenn die Temperatur weiter sinkt, wird durch einen stetigen Wandel der Kristallstrukturen mehr Volumen benötigt. Wenn die Temperatur steigt, benötigen die Moleküle wieder mehr Bewegungsfreiraum, wodurch das Volumen ebenfalls steigt.

Die Lebensdauer der einzelnen Cluster ist temperaturabhängig und liegt bei 4 °C in der Größenordnung von nur wenige billionstel Sekunden. Bei weiterer Abkühlung wird der instabile Zustand der Cluster aufgrund der abnehmenden Wärmebewegung immer stabiler, bis sich beim Erstarren schließlich stabile hexagonale Kristallstrukturen gebildet haben (Eis). Das Volumen nimmt bei diesem Phasenübergang nochmals deutlich zu.

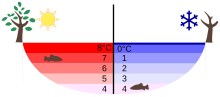
Die Dichteanomalie des Wassers ist wichtig für das Leben in Gewässern kälterer Klimazonen. Unterhalb einer Temperatur von etwa 4 °C sinkt Oberflächenwasser nicht nach unten. Statt des damit verbundenen Auskühlens tieferer Gewässerschichten und eines vollständigen Durchfrierens von unten her können sich thermische Schichten bilden. Wassertiere und -pflanzen können unter der Eisschicht überleben.

Die Temperatur, bei der Wasser die größte Dichte erreicht, sinkt mit steigendem Druck von 3,98 °C (1 bar) über ca. 2 °C (100 bar) auf ca. 0 °C (200 bar, wobei hier der Gefrierpunkt seinerseits auf −1,5 °C gesunken ist).

Zahlenwerte zu Dichteanomalie und Ausdehnungskoeffizient von Eis und Wasser bei Normaldruck

Der berechnete Ausdehnungskoeffizient ist ein mittlerer Ausdehnungskoeffizient zwischen beiden Temperaturen.

Substanz	$T_{0}$ / $T_{2}$ in [°C]	$\rho _{0}$ / $\rho _{2}$ in [g/cm³]	$\Delta T$ in [K]	mittlere Temperatur $T_{mittl.}$ in [°C]	$\gamma _{mittl.}$ in [1/K]
Wasser	0 / 0	0,918 (Eis) / 0,999840 (Wasser)	0	0	-
	0 / 1	0,918 (Eis) / 0,999899	1	0,5	-0,0819 !
	0 / 1	0,999840 (Wasser) / 0,999899	1	0,5	−0,000059006
	1 / 2	0,999899 / 0,999940	1	1,5	-0,0000410025
	2 / 3	0,999940 / 0,999964	1	2,5	-0,0000240009
	3 / 3,983 (Dichtemaximum !)	0,999964 / 0,999975	0,983	3,4915	-0,0000119051
	3 / 4	0,999964 / 0,999972	1	3,5	-0,00000800023
	3,983 (Dichtemaximum !) / 4	0,999975 / 0,999972	0,017	3,9915	+0,000176476
	3 / 5	0,999964 / 0,999964	2	4 (nah am Dichtemaximum !)	0
	4 / 5	0,999972 / 0,999964	1	4,5	+0,00000800028
	5 / 6	0,999964 / 0,999940	1	5,5	+0,0000240014
	6 / 7	0,999940 / 0,999901	1	6,5	+0,0000390039
	17 / 19	0,998773 / 0,998403	2	18	+0,0001853
	19 / 21	0,998403 / 0,997991	2	20	+0,0002064
	24 / 26	0,997295 / 0,996782	2	25	+0,0002573

Schmilzt Eis bei 0 °C zu Wasser, so nimmt dessen Volumen um etwa 8,19 % dabei ab. Beim Gefrieren nimmt es entsprechend um ca. 8,92 % zu.

Die mittleren Ausdehnungskoeffizienten $\gamma _{mittl.}$ wurden aus den Dichtewerten berechnet:

$\gamma _{mittl.}={\bar {\gamma }}={\frac {\Delta {V}}{V_{0}\cdot \Delta {T}}}={\frac {({\frac {V_{2}}{V_{0}}})-1}{\Delta {T}}}={\frac {({\frac {v_{2}}{v_{0}}})-1}{\Delta {T}}}={\frac {({\frac {\rho _{0}}{\rho _{2}}})-1}{\Delta {T}}}$

Dichteanomalie und (nicht isobarer) Ausdehnungskoeffizient von flüssigem Ammoniak

Bei jeder Temperatur hat das Flüssiggas einen anderen Dampfdruck, entsprechend seiner Dampfdruckfunktion. Daher erfolgt hier die temperaturbedingte Ausdehnung oder Kontraktion des Volumens nicht isobar.

Die negativen Ausdehnungskoeffizienten sind fett markiert.

Der berechnete Ausdehnungskoeffizient ist ein mittlerer Ausdehnungskoeffizient zwischen beiden Temperaturen.

Substanz	$T_{0}$ / $T_{2}$ in [°C]	$\rho _{0}$ / $\rho _{2}$ in [g/cm³]	$\Delta T$ in [K]	mittlere Temperatur $T_{mittl.}$ in [°C]	$\gamma _{mittl.}$ in [1/K]
flüssiges Ammoniak, siedend (beim eigenen Dampfdruck)	−70 / −68	0,72527 / 0,72036	2	−69	+0,003408
	−68 / −66	0,72036 / 0,72067	2	−67	-0,000215
	−66 / −64	0,72067 / 0,71839	2	−65	+0,001587
	−64 / −62	0,71839 / 0,71608	2	−63	+0,001613
	−50 / −48	0,70200 / 0,69964	2	−49	+0,001687
	−30 / −28	0,67764 / 0,67517	2	−29	+0,001829
	−28 / −26	0,67517 / 0,67263	2	−27	+0,001888
	−26 / −24	0,67263 / 0,67463	2	−25	-0,001482
	−24 / −22	0,67463 / 0,68587	2	−23	-0,008194
	−22 / −20	0,68587 / 0,66503	2	−21	+0,015668
	0−2 / 0	0,64127 / 0,63857	2	0−1	+0,002114
	0−2 / 2	0,64127 / 0,63585	4	000	+0,002131
	000 / 2	0,63857 / 0,63585	2	001	+0,002139
	018 / 20	0,61320 / 0,61028	2	019	+0,002392
	018 / 22	0,61320 / 0,60731	4	020	+0,002425
	020 / 22	0,61028 / 0,60731	2	021	+0,002445
	024 / 26	0,60438 / 0,60132	2	025	+0,002544
	048 / 50	0,56628 / 0,56306	2	049	+0,002859

Hinweis: Dichtewerte und Ausdehnungskoeffizienten des flüssigen Ammoniaks weisen im betrachteten Temperaturbereich zwei Dichteanomalien auf!

Die mittleren Ausdehnungskoeffizienten $\gamma _{mittl.}$ wurden aus den Dichtewerten berechnet:

Die Dichtequotienten sind den Volumenquotienten oder den Quotienten der spezifischen Volumina v (massenspezifisch oder molares Volumen) jeweils indirekt proportional!

Basierend auf einem Artikel in:

Wikipedia.de