Erweiterter euklidischer Algorithmus
Der erweiterte euklidische Algorithmus ist ein Algorithmus aus dem mathematischen
Teilgebiet der Zahlentheorie.
Er berechnet neben dem größten
gemeinsamen Teiler
zweier natürlicher
Zahlen
und
noch zwei ganze
Zahlen
und
,
die die folgende Gleichung erfüllen:
Der Algorithmus ist eine Erweiterung des bereits in der Antike bekannten euklidischen Algorithmus, der nur den größten gemeinsamen Teiler berechnet.
Das Haupteinsatzgebiet des erweiterten euklidischen Algorithmus ist
die Berechnung
der inversen Elemente in ganzzahligen
Restklassenringen, denn wenn der Algorithmus das Tripel
ermittelt, ist entweder
und damit
,
also das multiplikative Inverse von
modulo
oder aber
was bedeutet, dass
modulo
kein Inverses hat. Dies ist die Grundlage für die Lösung von diophantischen
Gleichungen oder allgemeiner von ganzzahligen linearen Gleichungssystemen.
Ebenso ist die Bestimmung inverser Elemente eine Grundlage für den chinesischen
Restsatz, welcher wiederum Grundlage des bedeutenden Tricks der kleinen
Primzahlen in der berechenbaren Algebra ist. Dabei wird eine Aufgabe in mehreren
endlichen Körpern gelöst und diese Teillösungen in immer größere
Restklassenringe gehoben, bis sich eine ganzzahlige Lösung ablesen lässt. Der
Algorithmus liefert zudem einen konstruktiven Beweis für das Lemma von Bézout.
Funktionsweise am Beispiel
Die am weitesten bekannte Version des euklidischen Algorithmus bezieht sich auf den Bereich der ganzen Zahlen. Jedoch kann er wortwörtlich auf jeden Ring angewandt werden, in welchem eine Division mit kleinstem Rest durchgeführt werden kann. Solche Ringe werden euklidisch genannt, ein Beispiel ist der Polynomring in einer Variablen mit rationalen oder reellen Koeffizienten. In diesem kann immer ein eindeutig bestimmter Rest mit kleinstem Grad gefunden werden.
Betrachten wir ein Beispiel. Zu der Vorgabe der Zahlen 99 und 78 produziert der einfache euklidische Algorithmus die Folge von Divisionen mit Rest:
3 ist ein Teiler von 6 und damit der gesuchte größte gemeinsame Teiler von 99 und 78. Nun kann man diese Gleichungen rückwärts lesen und den Rest jeweils als Differenz der beiden anderen Terme darstellen. Setzt man diese Restdarstellungen rekursiv ineinander ein, so ergeben sich verschiedene Darstellungen des letzten Restes 3:
Der größte gemeinsame Teiler ist so als ganzzahlige Linearkombination der beiden Ausgangszahlen 78 und 99 dargestellt.
In der eben dargestellten Berechnungsvorschrift muss man erst den letzten Schritt des einfachen euklidischen Algorithmus abwarten, bevor die Berechnung der gesuchten Koeffizienten beginnen kann. Man kann aber auch ebenso alle anderen Reste als ganzzahlige Linearkombination von 78 und 99 darstellen und die zugehörigen Koeffizienten in jedem Schritt des einfachen euklidischen Algorithmus mit bestimmen:
Tabellarische Darstellung
Rekursive Variante
Die Zwischenergebnisse beider Berechnungsmöglichkeiten lassen sich übersichtlich in Tabellen darstellen. Für die erste Variante, bei der die Folge der Divisionen mit Rest rückwärts aufgearbeitet wird, kann dies die folgende Gestalt annehmen:
|
|
|
Dabei wird zuerst, wie in der linken Tabelle, der einfache euklidische
Algorithmus ausgeführt. Die Division mit Rest hat dabei immer die Form
(anders gesagt, bei
handelt es sich um das Ergebnis der Ganzzahldivision von
durch
,
mit Rest
),
wobei
und
bestimmt werden.
wird in der Zeile vermerkt, das Paar
wird an die Stelle des Paars
in der nächsten Zeile eingetragen. Dieser Schritt wird solange wiederholt, bis
in der Spalte von
eine Null steht.
Bis zu diesem Punkt wurde der einfache euklidische Algorithmus ausgeführt,
und in der linken unteren Ecke (Spalte )
kann der größte gemeinsame Teiler abgelesen werden. In unserem Fall die Drei.
Nun beginnt die Berechnung der ganzzahligen Koeffizienten
und
.
In jeder Zeile soll dabei
gelten. Dementsprechend wird in der letzten Zeile
eingetragen, denn
.
Da in der letzten Zeile der Spalte
steht, kann für
ein beliebiger Wert genommen werden, denn
.
Hier im Beispiel ist
gesetzt, es ergibt sich die mittlere Tabelle.
Nun arbeitet man sich von unten nach oben. Für das
nimmt man das
der darunterliegenden Zeile. Das
berechnet sich aus dem
der jeweiligen Zeile und dem
und
der darunterliegenden Zeile.
bzw.
Für die vorletzte Zeile ergibt sich so
und
,
darüber dann
und
usw.
Diesen Schritt wiederholen wir solange, bis die Tabelle ausgefüllt ist. Es
ergibt sich die rechte Tabelle. Die Einträge für
und
in der ersten Zeile sind die gesuchten Werte. Der größte gemeinsame Teiler
findet sich, wie schon erwähnt, in der unteren linken Ecke. Für das Beispiel
gilt damit
Iterative Variante
Gegeben sind wieder die Werte 99 und 78:
Wie sich aus dem Beispiel ablesen lässt, hängt der aktuelle Rechenschritt von
den Zwischenergebnissen der zwei vorhergehenden Rechenschritte ab. Dem kann
Rechnung getragen werden, indem bei der Initialisierung eine Hilfszeile
vorangestellt wird. Weiter werden, der Übersicht halber, Hilfsvariablen
und
mit einer eigenen Spalte eingefügt.
|
Um die jeweils nächste Zeile zu bestimmen, werden folgende Operationen ausgeführt:
- Es wird die Division mit Rest ausgeführt,
und
sowie
gesetzt.
- Die neuen Werte der Hilfsvariablen werden aus der aktuellen Zeile
übernommen,
und
.
- Die neuen Koeffizienten ergeben sich durch
und
Durch diese Vorschrift gelten in jeder außer der ersten Zeile die Beziehungen
und
,
hier mit den Ausgangswerten
und
.
Aus den letzten zwei Zeilen liest man daher ab, dass 3 der größte
gemeinsame Teiler ist und
gilt.
Ist man mit dieser Methode vertraut genug, so kann man in der Tabelle die
Spalten
und
weglassen, da diese nur bereits weiter oben stehende Einträge wiederholen.
Weitere Beispiele in dieser verknappten Form sind in den folgenden Tabellen
dargestellt:
|
|
Allgemeine mathematische Grundlage
Der euklidische Algorithmus erzeugt zu vorgegebenen ganzen Zahlen a
und b (allgemein: Elementen eines euklidischen Rings) zwei Folgen: eine
Folge
von Quotienten und eine Folge
von Resten, wobei
.
In jedem Schritt
gilt dabei
,
.
Nach endlich vielen Schritten ergibt sich der Rest Null.
Wir gehen nun zu Restklassen
modulo b über. Es ist trivial zu sehen, dass
und
Vielfache von
nach Hinzufügen oder Abziehen von Vielfachen von
sind. Genauer sind die Restklassen
Vielfache der Restklasse
für
,
und nach Rekursionsvorschrift auch für
.
Es kann also eine Folge von Multiplikatoren
konstruiert werden, die mit
und
initialisiert ist, so dass
gilt. Es ergibt sich die rekursive Beziehung
.
Man kann diese Rekursion in folgende Abfolge von Schritten für den erweiterten euklidischen Algorithmus fassen:
- Erhalte
und
als Eingabe.
- Setze
,
,
und
.
- Wiederhole:
- Erhöhe
um eins.
- Bestimme den ganzzahligen Quotienten
.
- Setze
und
.
- Erhöhe
- bis
gilt.
- Gib den Rest
und die Zahl
mit
zurück.
Jeder Schritt enthält implizit auch einen Multiplikator ,
wobei diese Division keinen Rest lässt. Die Folge
kann auch explizit bestimmt werden, es gelten
,
und
.
Nach dem letzten Schritt ergibt sich nun
Der Übersicht halber werden beim händischen Rechnen auch noch die Hilfsfolgen
und
sowie
sowie
mitgeführt.
Algorithmische Umsetzung
Rekursive Variante
Für den erweiterten euklidischen Algorithmus existiert auch eine rekursive Variante, die durch den folgenden Pseudocode gegeben ist:
a,b: zwei Zahlen für die der erweiterte euklidische Algorithmus durchgeführt wird
extended_euclid(a,b) 1 wenn b = 0 2 dann return (a,1,0) 3 (d',s',t')extended_euclid(b, a mod b) 4 (d,s,t)
(d',t',s' – (a div b)t') 5 return (d,s,t)
Gleichbedeutend ist folgende mathematische Funktionsdefinition mit Fallunterscheidung:
Tricks zur effizienten Computerimplementierung
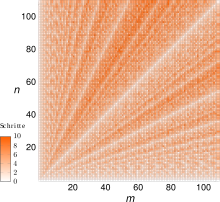
Darstellung mittels Matrizen
Versieht man die Variablen des euklidischen Algorithmus mit Indizes für den
Iterationsschritt, so wird im Schritt
die Division mit Rest
ausgeführt. Im Übergang zum nächsten Schritt wird
und
gesetzt. Bildet man aus
und
einen Spaltenvektor,
so hat der gesamte Schritt eine Darstellung mit Übergangsmatrix,
.
Terminiert der Algorithmus nach
Schritten, so gilt
und daher
.
Setzt man die Bildungsvorschriften der Spaltenvektoren ineinander ein, so ergibt
sich die Verbindung zwischen dem ersten und dem letzten Spaltenvektor durch ein
Matrizenprodukt,
.
Durch Multiplikation mit dem Zeilenvektor
wird die erste Zeile auf beiden Seiten extrahiert, somit gilt
.
Die verschiedenen Arten, das Matrixprodukt der letzten Identität
auszurechnen, ergeben die verschiedenen Varianten des erweiterten euklidischen
Algorithmus. In der klassischen Variante, in welcher die Divisionen mit Rest von
der letzten beginnend ausgewertet werden, entspricht der Bildung der
Matrixprodukte beginnend von links. Diese entspricht dem nachfolgenden
rekursiven Algorithmus. Es wird
gesetzt und rekursiv
für
bestimmt. Am Ende gilt .
Es müssen aber zuerst alle Quotienten bestimmt werden, bevor der erste
Rekursionsschritt ausgeführt werden kann.
Beginnt man die Produktbildung von rechts, so wird der Quotient der Division mit Rest in dem Augenblick benutzt, in dem er bestimmt wurde und kann danach vergessen werden. Dies entspricht dem am Anfang angegebenen Algorithmus, in welchem am Anfang
festgesetzt und
für
iteriert wird. Insgesamt ergibt sich damit
.
Am Ende gilt ,
wobei wegen der Beziehungen
und
der letzte Iterationsschritt auch weggelassen werden kann.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2020