Quasiordnung

Eine Quasiordnung, auch Präordnung, (englisch preorder) ist eine abgeschwächte Variante einer Halbordnung, bei der es möglich ist, dass verschiedene Elemente in beiden Richtungen vergleichbar sind. Die Antisymmetrie muss also nicht erfüllt sein.

Jede beliebige zweistellige Relation kann zu einer Quasiordnung erweitert werden, indem man ihre reflexiv-transitive Hülle bildet.

Insbesondere die totalen Quasiordnungen treten in praktischen Anwendungen beim Anordnen von Objekten in Sortierverfahren, Tabellenkalkulationsprogrammen oder Datenbanken auf.

Definitionen

Quasiordnung

4 Typen von Ordnungsrelationen in Beziehung: A ${\rightarrow }$ B: A ist B; A ${\color {Green}\downarrow }$ B: aus A wird B bei Quotientenbildung; A ${\color {Red}\uparrow }$ B: aus A wird B bei Erweiterung; A ${\color {Blue}\rightarrow }$ B: aus A wird B bei komponentenweiser Komposition

Eine zweistellige Relation $\lesssim$ auf einer Menge $M\$ heißt eine Quasiordnung (englisch preorder), wenn sie reflexiv und transitiv ist. Für alle $a,b,c\in M$ muss also gelten

$a\lesssim a$	(Reflexivität)
$a\lesssim b\lesssim c\implies a\lesssim c$	(Transitivität)

Man nennt dann $(M,\lesssim )$ eine quasigeordnete Menge oder kurz eine Quasiordnung.

Totale Quasiordnung

Eine Quasiordnung heißt total, auch Präferenzordnung, (englisch total preorder), wenn je zwei Elemente immer vergleichbar sind. Für alle $a,b\in M$ muss also gelten:

$a\lesssim b\;\;\vee \;\;b\lesssim a$

(Totalität)

Man nennt dann $(M,\lesssim )$ eine total quasigeordnete Menge oder kurz eine totale Quasiordnung.

Eigenschaften

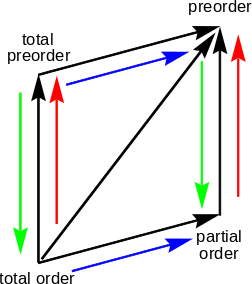
Eine Halbordnung (englisch partial order) ist eine Quasiordnung.

Eine Totalordnung (englisch total order) ist eine totale Quasiordnung (und auch eine Halbordnung).

Jede Äquivalenzrelation ist eine Quasiordnung.

Ist $(M,\lesssim )$ eine Quasiordnung, dann gilt für alle $a,b\in M$
$a\lesssim b\iff \forall x\in M\colon (x\lesssim a\Rightarrow x\lesssim b)$ .
Diese Eigenschaft ist sogar charakterisierend für Quasiordnungen: jede Relation $\lesssim$ mit dieser Eigenschaft ist eine Quasiordnung.

Ist $(M,\lesssim )$ eine Quasiordnung, dann gilt $a\lesssim b\wedge b\lesssim a$ genau dann, wenn für alle
$x\lesssim a\iff x\lesssim b$
gilt.

Beispiele und Gegenbeispiele

Vergleicht man komplexe Zahlen anhand ihres Betrags, erhält man eine totale Quasiordnung. Deren Definition lautet also: $a\lesssim b:\Longleftrightarrow |a|\leq |b|$ . Dies ist keine Halbordnung, da zum Beispiel die Zahlen und $\mathrm {i}$ gegenseitig vergleichbar sind, also $1\lesssim {\mathrm {i}}$ und ${\mathrm {i}}\lesssim 1$ gilt.
Auf der Knotenmenge eines gerichteten Graphen erhält man eine Quasiordnung durch die Festlegung
$a\lesssim b:\Longleftrightarrow$ es gibt einen gerichteten Weg von nach ( ist also von aus erreichbar).
Diese Quasiordnung ist genau dann eine Halbordnung, wenn der Graph zyklenfrei (azyklisch) ist, also keine oder nur triviale Zyklen enthält.
Tatsächlich lässt sich jede endliche Quasiordnung auf diese Weise aus einem geeigneten Graphen gewinnen.
Die Teilbarkeitsrelation | ist eine Quasiordnung auf der Menge der ganzen Zahlen. Sie ist keine Halbordnung, da zum Beispiel 3 | -3, aber auch -3 | 3 gilt. Betrachtet man die Teilbarkeit auf der Menge der natürlichen Zahlen, kommt die Antisymmetrie hinzu, so dass eine Halbordnung vorliegt.
Ist das Vergleichen von (reellen oder rationalen) Zahlen mit einer Schwankungsbreite (Ungenauigkeit) behaftet, dann handelt es sich nicht um eine Quasiordnung, da die zugehörige Duplikatrelation keine Äquivalenzrelation ist.
Dagegen ist das Vergleichen nach Abschneiden von Dezimal- oder Binärstellen, oder allgemeiner nach Rundung, eine totale Quasiordnung.
Die Normen für die alphabetische Sortierung im Deutschen sind bei der Groß-/Kleinschreibung und der Behandlung von Umlauten Beispiele für totale Quasiordnungen, die keine Totalordnungen sind.

Induzierte Äquivalenzrelation und Striktordnung

Eine Quasiordnung $\lesssim$ auf einer Menge $M\$ erzeugt eine Äquivalenzrelation – die „kanonische“, das heißt die zu $\lesssim$ gehörige, ausgezeichnete Äquivalenzrelation – $\sim$ auf $M\$ durch die Festlegung

$a\sim b:\Longleftrightarrow a\lesssim b\wedge b\lesssim a$ .

Zwei Elemente sind also äquivalent, wenn sie gegenseitig vergleichbar sind. Diese Äquivalenzrelation sei der Kürze halber als Duplikatrelation der Quasiordnung bezeichnet. Ist $\lesssim$ bereits eine Äquivalenzrelation, entsteht durch diese Konstruktion wieder $\lesssim$ .

Die Nebenklasse von ist die Menge

${\bar a}:=\{x\mid x\sim a\}$ .

Weiterhin erhält man die kanonische Striktordnung $<\$ auf $M\$ vermöge

$a<b:\Longleftrightarrow a\lesssim b\wedge a\not \sim b$ .

Ist $\lesssim$ total, dann ist $<\$ eine strenge schwache Ordnung. Generell ist das Komplement einer totalen Quasiordnung eine strenge schwache Ordnung, und umgekehrt.

Zwischen der Ursprungsrelation und den 2 induzierten Relationen besteht der folgende Zusammenhang:

$a\lesssim b\Longleftrightarrow a\sim b\vee a<b\$ ,

wobei die zwei Bedingungen auf der rechten Seite sich gegenseitig ausschließen.

Beispiele:

Vergleicht man komplexe Zahlen anhand ihres Betrags (siehe oben), dann sind zwei Zahlen genau dann äquivalent, wenn ihr Betrag gleich ist. Die Äquivalenzklassen sind also die Kreise um den Nullpunkt in der komplexen Ebene. Eine Zahl ist „kleiner“ als eine zweite, wenn sie auf dem Kreis mit kleinerem Radius liegt (Radius 0 ist zugelassen).

Ein gerichteter Graph

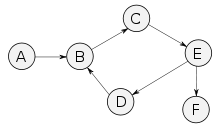
Bei der durch einen gerichteten Graphen gegebenen Quasiordnung (siehe oben) sind zwei Knoten genau dann äquivalent, wenn sie gleich sind oder auf einem gemeinsamen Zyklus liegen. Weiterhin gilt , wenn es zwar einen gerichteten Weg von nach , aber keinen gerichteten Weg von nach gibt. Die drei Äquivalenzklassen beim nebenstehenden Graphen sind also $\left\{A\right\},\left\{B,C,D,E\right\},\left\{F\right\}.$ Außerdem gilt für die induzierte strenge Halbordnung: $A<B,C,D,E<F.$

Die Teilbarkeitsrelation ist auch eine Quasiordnung auf jedem Integritätsring. Zwei Elemente sind genau dann äquivalent (im Sinne der Quasiordnung), wenn sie assoziiert sind, also durch Multiplikation mit einer Einheit auseinander hervorgehen.

Quotientenmenge

Auf der Quotientenmenge oder Faktormenge $M/\!\sim$ (also der Menge der Äquivalenzklassen) erhält man die kanonische Halbordnung durch die wohldefinierte Festlegung

$[x]\leq [y]:\Longleftrightarrow x\lesssim y$

(wobei die Klasse von $x\$ mit $[x]\$ bezeichnet ist).

Ist die gegebene Quasiordnung total, dann ist das Ergebnis eine Totalordnung.

Beispiele:

Beim Vergleich komplexer Zahlen anhand ihres Betrags (siehe oben) ist die Halbordnung auf der Quotientenmenge isomorph zur gewöhnlichen (totalen) Ordnung $\leq \$ auf den nichtnegativen reellen Zahlen.
Bei der Teilbarkeitsrelation auf den ganzen Zahlen (siehe oben) ist die Halbordnung auf der Quotientenmenge isomorph zur Teilbarkeitsrelation auf der Menge der natürlichen Zahlen (einschließlich 0).

Spiegelung

Eine Quasiordnung $(M,\lesssim )$ kann gespiegelt werden:

$a\lesssim _{2}b:\Longleftrightarrow \ b\lesssim a\;\;$ (siehe auch Umkehrrelation).

Normalerweise nimmt man dann die Schreibweise:

$a\gtrsim b:\Longleftrightarrow \ b\lesssim a$ .

Ist die gegebene Quasiordnung total, dann ist auch das Ergebnis total.

Ist sie eine Halbordnung, so auch das Ergebnis.

Die Spiegelung der Spiegelung ist das Original.

Komposition (Zusammensetzung, Hintereinanderschaltung)

komponentenweise Zusammensetzung

Auf zwei quasigeordneten Mengen $(M_{1},\lesssim _{1})$ und $(M_{2},\lesssim _{2})$ kann die Zusammensetzung komponentenweise-kleiner-oder-gleich $\lesssim _{1}\!\oplus \!\lesssim _{2}$ auf der Menge $M_{1}\!\times \!M_{2}$ der Paare wie folgt definiert werden:

${\left(a_{1},a_{2}\right)}\;\;\lesssim _{1}\!\oplus \!\lesssim _{2}\;\;{\left(b_{1},b_{2}\right)}\;\;\;:\Longleftrightarrow \;\;\;a_{1}\lesssim _{1}b_{1}\wedge a_{2}\lesssim _{2}b_{2}$

Die Zusammensetzung $(M_{1}\!\times \!M_{2},\lesssim _{1}\!\oplus \!\lesssim _{2})$ ist wieder eine Quasiordnung.

Asymmetrie bleibt erhalten. Totalität geht jedoch verloren, das heißt, bei zwei totalen Quasiordnungen bleibt nur eine Quasiordnung, bei zwei Totalordnungen nur eine Halbordnung übrig. (Beispiel: (1,0) ist nicht vergleichbar mit (0,1).)

Eine Art Kommunitativität ist vorhanden, denn $(M_{2}\!\times \!M_{1},\lesssim _{2}\!\oplus \!\lesssim _{1})$ ist isomorph zu $(M_{1}\!\times \!M_{2},\lesssim _{1}\!\oplus \!\lesssim _{2})$ .

Lexikographische Zusammensetzung

Auf zwei quasigeordneten Mengen $(M_{1},\lesssim _{1})$ und $(M_{2},\lesssim _{2})$ kann die lexikographische Zusammensetzung $\lesssim _{1}\!\otimes \!\lesssim _{2}$ auf der Menge $M_{1}\!\times \!M_{2}$ der Paare wie folgt definiert werden:

${\left(a_{1},a_{2}\right)}\;\;\lesssim _{1}\!\otimes \!\lesssim _{2}\;\;{\left(b_{1},b_{2}\right)}\;\;\;:\Longleftrightarrow \;\;\;a_{1}<_{1}b_{1}\vee (a_{1}\sim _{1}b_{1}\wedge a_{2}\lesssim _{2}b_{2})$

Die Zusammensetzung $(M_{1}\!\times \!M_{2},\lesssim _{1}\!\otimes \!\lesssim _{2})$ ist wieder eine Quasiordnung. (Für die Ordnung der gleich langen Wörter unten sei der Einfachheit halber wieder $\lesssim _{1}\!\otimes \!\lesssim _{2}\,\,=:\,\,\lesssim$ gesetzt.)

Nach dem lexikographischen Prinzip lassen sich folgende Quasiordnungen für variabel lange Symbolsequenzen ableiten:

Sei $(M,\lesssim )$ quasigeordnet und seien $l_{a}:=\operatorname {length}(a)$ und $l_{b}:=\operatorname {length}(b)$ die Längen zweier Wörter $a,b\in M^{*}$ (Kleenesche Hülle) und $m:=\operatorname {min}(l_{a},l_{b})$ , dann kann $M^{*}\$ sowohl durch:

$a\lesssim _{q}b\;:\Longleftrightarrow \ l_{a}<l_{b}\,\,\,\vee \,\,\,(l_{a}=l_{b}\,\wedge \,\operatorname {left}(a,m)\lesssim \operatorname {left}(b,m))$ ^[1]

als auch durch:

$a\lesssim \ b\;:\Longleftrightarrow \ \operatorname {left}(a,m)<\ \operatorname {left}(b,m)\,\,\,\vee \,\,\,(\operatorname {left}(a,m)\sim \operatorname {left}(b,m)\,\wedge \,l_{a}\leq l_{b})$

quasigeordnet werden. Letztere Zusammensetzung nennt man wieder lexikographisch.

Sind die gegebenen Quasiordnungen alle total (auf ihren jeweiligen Komponentmengen), und nur dann, entsteht wieder eine totale Quasiordnung.

Sind sie allesamt sogar Totalordnungen, entsteht wieder eine Totalordnung.

Assoziativität

Die genannten Zusammensetzungen verhalten sich assoziativ, das heißt $(\lesssim _{1}\!\oplus \!\lesssim _{2})\oplus \!\lesssim _{3}\,=\,\lesssim _{1}\!\oplus (\lesssim _{2}\!\oplus \!\lesssim _{3})$ und $(\lesssim _{1}\!\otimes \!\lesssim _{2})\otimes \!\lesssim _{3}\,=\,\lesssim _{1}\!\otimes (\lesssim _{2}\!\otimes \!\lesssim _{3})$ .

Bemerkung:

Bei den Tabellenkalkulationsprogrammen entspricht eine „Spalte“ einer Komponentmenge $M_{i}\$ . Die in diesen Programmen häufig angebotene Sortierfunktion entspricht einer lexikographischen Zusammensetzung mit zu spezifizierender Rangfolge der Spalten, wobei es in der Regel zu jeder Spalte eine „Standard“-Ordnung gibt, die meist eine totale Quasiordnung, seltener eine echte Totalordnung (und dann höchstens auf der entsprechenden Spalte) ist. Es kann die „aufsteigende“ oder „absteigende“ Sortierreihenfolge gewählt werden.

Urbild einer Ordnungsrelation

Sei $M_{0}\$ eine nicht-leere Menge, $(M,\lesssim )$ eine quasigeordnete Menge und $f\colon \,M_{0}\to M$ eine beliebige Abbildung. Dann kann vermöge

$a_{0}\lesssim _{f}b_{0}:\Longleftrightarrow f(a_{0})\lesssim f(b_{0})$

die Menge $(M_{0},\lesssim _{f})$ quasigeordnet werden.

Ist $(M,\lesssim )$ total quasigeordnet, so ist es auch $(M_{0},\lesssim _{f})$ .

Ist $(M,\lesssim )$ eine Halbordnung, so ist $(M_{0},\lesssim _{f})$ eine Halbordnung genau dann, wenn $f\$ injektiv ist.

Bemerkung:

Seit 1991 gibt es für die digitale Codierung der Alphabete die internationale Norm des Unicode, die sich immer stärker durchzusetzen scheint. Über die Anordnung der Zeichen ist damit noch nicht allzu viel ausgesagt, da hier neben Sonderproblematiken wie den Umlauten zum Beispiel auch die Beachtung/Nichtbeachtung der Groß-/Kleinschreibung und Sonderzeichen die Abbildung zu einer nicht-injektiven machen kann.

Erweiterung

Ist $(M_{1},\lesssim )$ eine Quasiordnung und $M_{2}\$ eine beliebige nicht-leere Menge, so kann $\lesssim$ wie folgt auf die Menge $M_{1}\!\times \!M_{2}$ erweitert werden:

${\left(a_{1},a_{2}\right)}\lesssim _{2}{\left(b_{1},b_{2}\right)}\;\;\;:\Longleftrightarrow \;\;\;a_{1}\lesssim b_{1}$ .

Wie $\lesssim$ ist auch $(M_{1}\!\times \!M_{2},\lesssim _{2})$ eine Quasiordnung.

Ist $\lesssim$ total, so ist das Ergebnis wieder eine totale Quasiordnung.

Antisymmetrie geht im Allgemeinen verloren, das heißt, wenn die gegebene Quasiordnung $\lesssim$ eine Halbordnung (bzw. Totalordnung) ist, ist das Ergebnis nur dann wieder eine Halbordnung (bzw. Totalordnung), wenn $M_{2}\$ aus genau einem Element besteht. Besteht $M_{2}\$ aus mehreren Elementen, so ist das Ergebnis nur noch eine Quasiordnung (bzw. totale Quasiordnung).

$\lesssim _{2}$ ist die Quasiordnung $(\lesssim \!\otimes \,\tau )$ (mit der trivialen Ordnung $\tau \$ auf $M_{2}\,$ ). Man kann sich $\lesssim$ als eine Vergleichsfunktion vorstellen, die auf ihren Schlüsselfeldern in $M_{1}\$ operiert. Die Ergebnisordnung kann also ohne Verlust an Genauigkeit wieder mit $(M_{1}\!\times \!M_{2},\lesssim )$ bezeichnet werden.

Zusammensetzung auf der Grundmenge

Hat man auf einer Menge mehrere Quasiordnungen $\lesssim _{1},\lesssim _{2},\ldots$ , so kann man ähnlich wie oben die lexikographischen Zusammensetzungen $(M,\lesssim _{1}\!\otimes \!\lesssim _{2}\!\otimes ...)$ bilden gemäß

$a\lesssim _{1}\!\otimes \!\lesssim _{2}b\;\;\;:\Longleftrightarrow \;\;\;a<_{1}b\vee (a\sim _{1}b\wedge a\lesssim _{2}b)$ .

Sie bilden eine (nicht-kommutative) Halbgruppe mit dem (beidseitig) neutralen Element $\tau$ .

$(M,\lesssim _{1}\!\otimes \!\lesssim _{2}\!)$ ist eine Verfeinerung von $(M,\lesssim _{1}\!)$ . Das heißt auch, dass eine einer (auf ganz totalen) Totalordnung nachgeschaltete Quasiordnung nichts mehr ändert.

Beispiel:

Sei $M:={\mathbb N}$ die Menge der natürlichen Zahlen, $\lesssim _{1}\;:=\;<_{{\varphi }}$ mit der (nicht-injektiven) Eulerschen $\varphi$ -Funktion und $\lesssim _{2}\;:=\;<$ die übliche Kleinerrelation, dann ordnet die Totalordnung $(\lesssim _{1}\!\otimes \!\lesssim _{2})\;=\;(<_{{\varphi }}\!\otimes \!<)$

die Zahlen	2,	3,	4,	5,	6,	7,	8,	9,	10,	11,	12	um
zu	2,	3,	4,	6,	5,	8,	10,	12,	7,	9,	11	wegen
	1,	2,	2,	2,	4,	4,	4,	4,	6,	6,	10	für die $\varphi$ -Werte.

Einschränkung einer Quasiordnung

In naheliegender Weise wird von einer Quasiordnung $(M_{1},\lesssim )$ die Einschränkung $(M_{2},\lesssim )$ auf eine Teilmenge $M_{2}\subseteq M_{1}$ gebildet.

Bemerkung:

Die Definitionsbereiche sind in der Regel konzeptionell unendliche Mengen. Insoweit können Aussagen über die Eigenschaften der Ordnungsrelationen (insbesondere über die Transitivität) nur aus mathematischen Überlegungen stammen. Die Belegungen in den Anwendungen der Informatik sind natürlich stets endlich.

Intervalle

Ähnlich wie bei den Zahlen lässt sich allgemeiner bei quasigeordneten Mengen ein Intervallbegriff einführen – in einer Notation, wie man sie von der Schule her kennt:

	$:=\{x\mid a\lesssim x\;\wedge \;x\lesssim b\}$
${[}a,b{)}:=\,{[}a,b{[}$	$:=\{x\mid a\lesssim x\;\wedge \;x<b\}$
${(}a,b{]}:=\,{]}a,b{]}$	$:=\{x\mid a<x\;\wedge \;x\lesssim b\}$
$(a,b):=\,{]}a,b{[}$	$:=\{x\mid a<x\;\wedge \;x<b\}$

Die Duplikatsklasse von ist dann ${\bar a}=[a,a]=:[a]$ .

Für uneigentliche Intervalle gibt es die Notationen:

${[}a,\;{)}\;:=\,{[}a,\;{[}$	$:=\,\{x\mid a\lesssim x\}$
$(a,\;)\,:=\,{]}a,\;{[}$	$:=\,\{x\mid a<x\}$
${(}\;,a{]}\;:=\,{]}\;,a{]}$	$:=\,\{x\mid x\lesssim a\}$
$(\;,a)\,:=\,{]}\;,a{[}$	$:=\,\{x\mid x<a\}$

Fußnoten

↑ auch als quasi-lexikographische Ordnung bezeichnet (im Englischen quasi-lexicographic, radix, length-plus-lexicographic oder shortlex order)

Siehe auch

transitive Hülle

Basierend auf einem Artikel in:

Wikipedia.de