Nichtlineare Optimierung

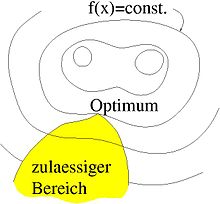
Nichtlineares Programm mit zulässigem Bereich und Optimum

In der Mathematik ist die nichtlineare Optimierung (auch nichtlineares Programm, NLP, genannt) das Vorhaben, eine skalare Zielfunktion einer oder mehrerer reeller Variablen in einem eingeschränkten Bereich zu optimieren, wobei die Zielfunktion oder die Bereichsgrenzen nicht linear (affin) sind. Es ist ein Teilgebiet der mathematischen Optimierung und ein Obergebiet der konvexen Optimierung. In Abgrenzung von den genannten Begriffen wird hier die Anwendung auf differenzierbare nichtlineare Zielfunktionen ohne Beschränkung auf Konvexität der Zielfunktion oder des Suchbereiches beschrieben. Unter Begriffe: Zielfunktion, Nebenbedingungen, zulässige Menge, lokale und globale Optimierung finden sich wesentliche Erklärungen.

Anwendungsfelder

Nichtlineare Programme finden sich in vielfältiger Weise in der Wissenschaft und im Ingenieurwesen.

In der Wirtschaftswissenschaft kann es darum gehen, die Kosten eines Prozesses zu minimieren, der Einschränkungen in der Verfügbarkeit der Mittel und Kapazitäten unterliegt. Die Kostenfunktion kann darin nichtlinear sein. In der theoretischen Mechanik findet sich im Hamiltonschen Prinzip ein Extremalprinzip, dessen Lösung bei nichtlinearen Randbedingungen ein nichtlineares Programm darstellt.

Moderne Ingenieuranwendungen beinhalten oft und in komplizierter Weise Optimierungsaufgaben. So kann es darum gehen, das Gewicht eines Bauteils zu minimieren, das gleichzeitig bestimmten Anforderungen (z.B. Einschränkungen des Bauraumes, Obergrenzen für Verformungen bei gegebenen Lasten) genügen muss.

Bei der Anwendung eines mathematischen Modells kann es darum gehen, die Parameter des Modells an gemessene Werte anzupassen. Nichtlineare Einflüsse der Parameter und Einschränkungen an die Parameter (z.B. dass nur positive Werte zugelassen sind) führen hier auf ein nichtlineares Programm.

In diesen Fragestellungen ist oftmals nicht a priori bekannt, ob das gestellte Problem konvex ist oder nicht. Manchmal beobachtet man eine Abhängigkeit der gefundenen optimalen Lösung vom Startpunkt der Suche. Dann hat man lokale Optima gefunden und das Problem ist mit Sicherheit nicht konvex.

Problemdefinition

Es gibt viele mögliche Formulierungen eines nicht linearen Programms. An dieser Stelle soll eine möglichst allgemeine Form gewählt werden. Der Eingabeparameter ${\vec {x}}$ sei aus dem $\mathbb {R} ^{n}$ , das heißt, das Problem hängt von Einflussparametern ab, die im Vektor ${\vec {x}}$ eingelagert sind. Die Zielfunktion $f\colon D\to\R$ sei einmal stetig differenzierbar. Weiterhin seien die Nebenbedingungen (NB) in Ungleichheitsform $g_{i}\colon D\to \mathbb {R}$ mit $1 \leq i \leq m$ und in Gleichheitsform $h_{k}\colon D\to \mathbb {R}$ mit $1\leq k\leq l$ gegeben und einmal stetig differenzierbar. Dann lautet das Problem mathematisch:

${\begin{array}{llll}P:&f({\vec {x}})&&\to \mathrm {extremum} \\f:&{\vec {x}}\in S\subset &D\subseteq \mathbb {R} ^{n}&\to \mathbb {R} \\S:&\{{\vec {x}}\in D\;|&g_{i}({\vec {x}})\leq 0&{\text{für}}\;1\leq i\leq m,\\&&h_{k}({\vec {x}})=0&{\text{für}}\;1\leq k\leq l\}\\\end{array}}$ .

Der zulässige Bereich wird von den Nebenbedingungen (NB) eingeschränkt: Für alle Werte der Parameter aus dem zulässigen Bereich ( ${\vec {x}}\in S$ ) sollen die NB erfüllt sein. Zulässig ist das Problem , wenn der zulässige Bereich nicht leer ist.

Zumeist beschränkt sich die theoretische Behandlung der nicht linearen Optimierung auf Minimierungsprobleme. In der Tat kann das Maximierungsproblem einer Funktion in ein Minimierungsproblem von oder 1/f , falls f>0 gesichert ist, umformuliert werden.

Vorgehen

Das Problem wird mit den unten beschriebenen Verfahren auf die Optimierung einer Hilfsfunktion ohne NB zurückgeführt. Um sich die gradientenbasierten Methoden zu Nutze machen zu können, teilt man das abzusuchende Gebiet gegebenenfalls in solche auf, in denen die Zielfunktion differenzierbar ist. Wenn möglich, sollten die Teilgebiete konvex sein und die Zielfunktion in ihnen auch. Dann kann man die globalen Extrema in den Teilgebieten mit den in Mathematische Optimierung und Konvexe Optimierung aufgeführten Verfahren berechnen und das optimale auswählen.

Die Konstruktion der Hilfsfunktion soll anhand eines Beispiels erläutert werden: Zwei Kugeln in einer Mulde versuchen den tiefstmöglichen Punkt einzunehmen, dürfen sich dabei aber nicht durchdringen. Die Zielfunktion ist also die Lageenergie der Kugeln und nimmt im Gleichgewicht ein Minimum an. Die Nebenbedingung $g(x,y)\leq 0$ würde hier die Durchdringung der Kugeln und bezeichnen, wobei mit negativer Durchdringung ein positiver Abstand gemeint wird.

Lagrange-Multiplikatoren: Die NB werden mit reellen Faktoren, den Lagrange-Multiplikatoren, multipliziert und in die Zielfunktion eingebaut, so dass bei positiven Lagrange-Multiplikatoren die Verletzung der NB bestraft wird. Die so erhaltene Hilfsfunktion heißt Lagrange-Funktion. Die Lagrange-Multiplikatoren werden als Unbekannte in das Problem eingeführt und müssen ebenfalls bestimmt werden. Bei den Kugeln sind die Lagrange-Multiplikatoren gerade die Kontaktkräfte, die die Kugeln bei Berührung aufeinander ausüben, so dass sie sich nicht durchdringen.
Barrierefunktionen: Die NB werden mit Barrierefunktionen dargestellt, die bei Annäherung an die Grenze des Definitionsbereiches positive Werte annehmen und auf der Grenze ins Unendliche wachsen. Die Barrierefunktionen werden mit Barriereparametern multipliziert und in die Zielfunktion eingebaut, so dass die Annäherung an die Grenze bestraft wird und so die Verletzung der NB verhindert wird. Im Kugelbild bekämen die Kugeln einen mehr oder weniger dicken Mantel, der immer steifer wird, je stärker er bei Berührung zusammengedrückt wird. Eine Verletzung der NB wird so verhindert zu dem Preis, dass bereits die Annäherung an die Bereichsgrenze bestraft wird. Die Methode wird bei Innere-Punkte-Verfahren angewendet.
Straffunktionen: Die Straffunktionen werden wie die Barrierefunktionen eingesetzt. Die NB werden mit Straffunktionen dargestellt, die im zulässigen Bereich verschwinden und bei Verletzung der NB positiv sind. Die Straffunktionen werden mit Strafparametern multipliziert und in die Zielfunktion eingebaut, so dass die Verletzung der NB bestraft wird, daher der Name. Hier werden aktive NB evtl. verletzt und die Zulässigkeit der Lösung muss geprüft werden. Im Kugel-Bild entspricht die Straffunktion der „echten“ Durchdringung (die bei positivem Abstand der Kugeln verschwindet) und der Strafparameter einer Federsteifigkeit. Die Feder versucht eindringende Punkte wieder an die Oberfläche zu ziehen. Je steifer die Feder ausfällt, desto geringer wird die Eindringung sein.
Erweiterte Lagrange-Methode (englisch augmented Lagrange method): Dies ist eine Kombination der Lagrange-Multiplikatoren und der Strafmethode. Der Lagrange-Multiplikator wird iterativ anhand der Verletzung der NB bestimmt.
Trivial (und deshalb in den Quellen oftmals nicht behandelt), aber doch zu erwähnen und im praktischen Gebrauch ist, dass aktive NB dazu genutzt werden können, Variable zu eliminieren. Die Variablen werden auf Werte festgelegt, derart dass eine Verletzung der NB nunmehr unmöglich ist. Im Kugel-Bild würde man Berührungspunkte der Kugeln aneinanderkoppeln (ihre Koordinaten gleichsetzen), so dass eine Durchdringung (dort) nicht mehr stattfinden kann.

Die Vor- und Nachteile der beschriebenen Methoden sind in der Tabelle zusammengefasst:

Methode	Vorteile	Nachteile
Lagrange-Multiplikatoren	Erfüllt die NB exakt Das Vorzeichen des Multiplikators zeigt an, ob die NB aktiv ist oder nicht.	Führt zusätzliche Unbekannte ein. Schleust verschwindende Diagonalglieder in das Gleichungssystem ein (problematisch bei Cholesky-Zerlegung).
Barrierefunktionen	Die NB werden eingehalten. Für $r\to 0$ geht die gefundene Lösung in die mit Lagrange-Multiplikatoren gefundene über.	Die Höhenlinien der Hilfsfunktion stimmen nicht mit denen der Zielfunktion überein. Im Extremfall gibt es für einige Werte von gar kein Optimum. Bei Annäherung an die Grenze des zulässigen Bereiches und mit $r\to 0$ ist die Hesse-Matrix schlecht konditioniert.
Strafverfahren	Für $r\to \infty$ geht die gefundene Lösung in die mit Lagrange-Multiplikatoren gefundene über.	Die Nebenbedingung wird nur näherungsweise erfüllt. Mit $r\to \infty$ ist die Hesse-Matrix schlecht konditioniert. Die Prüfung der Aktivität der NB kann nur durch Auswertung der Funktionen $g_{i}$ und erfolgen.
Erweiterte Lagrange-Methode	Mit zunehmender Anzahl an Iterationen geht die gefundene Lösung in die mit Lagrange-Multiplikatoren gefundene über. Erfüllt die NB beliebig genau. Das Vorzeichen des Multiplikators zeigt an, ob die Nebenbedingung aktiv ist oder nicht.	Benötigt mehrere konvergierte Lösungen des globalen Problems.
Eliminierung der Freiheitsgrade	Reduziert die Anzahl an Unbekannten. Hält Gleichheitsnebenbedingungen exakt ein.	Ist nur anwendbar, wenn die Aktivität der NB bekannt ist.

Theorie der Optimierung

Isolierte Punkte

In einem nicht linearen Programm können NB den zulässigen Bereich in einigen Punkten ${\vec {x}}$ derart einschränken, dass zwar ${\vec {x}}$ aber kein Punkt in seiner Umgebung $U_{{\varepsilon }}({\vec {x}})$ im zulässigen Bereich liegt. Mathematisch formuliert heißt das, dass es eine Umgebung $U_{{\varepsilon }}({\vec {x}})$ gibt, so dass

$U_{\varepsilon }({\vec {x}})\cap S=\lbrace {\vec {x}}\rbrace$

gilt. Isolierte Punkte müssen alle einzeln, jeder für sich, auf Optimalität geprüft werden.

Regularitäts-Bedingungen, Tangenten- und Linearisierender Kegel

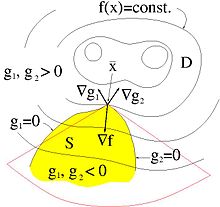
Beispiel eines Nicht Linearen Programms

Für die Formulierung von Optimalitätsbedingungen müssen die NB gewisse Anforderungen erfüllen, engl. constraint qualifications (CQ). Unter Anderem geht es darum, optimale Punkte aus der Betrachtung auszuschließen, die isoliert sind oder in denen es redundante NB gibt. Es existieren mehrere unterschiedlich scharfe Formulierungen, welche die Erfüllung dieser CQ sicherstellen. Punkte, in denen die Anforderungen erfüllt sind, heißen regulär. Irreguläre Punkte, in denen keine dieser Anforderungen greift, müssen ausgeschlossen oder gesondert betrachtet werden.

Zentral für die Formulierung der Anforderungen an die NB und der Optimalitätsbedingungen ist der Begriff Tangentenkegel $T(S,{\vec {x}})$ und Linearisierender Kegel. Um sich diese anschaulich klarzumachen, stellt man sich an einen Punkt ${\vec {x}}_{0}\neq {\vec {x}}$ im zulässigen Gebiet und läuft unter Beachtung der NB (die NB kann man sich als undurchdringliche Wände vorstellen) zum Zielpunkt ${\vec {x}}$ . Der Tangentenkegel ist dann die Menge aller möglichen Richtungen aus denen man im Zielpunkt ${\vec {x}}$ ankommen kann. Beim linearisierenden Kegel werden zunächst die NB linearisiert, d.h. durch ihre Tangenten im Zielpunkt ${\vec {x}}$ ersetzt. Der linearisierende Kegel ist dann die Menge aller möglichen Richtungen, aus denen man unter Beachtung der linearisierten NB im Zielpunkt ${\vec {x}}$ ankommen kann. Der Tangentenkegel und Linearisierende Kegel unterscheiden sich dort, wo zwei Wände am Standort parallel verlaufen und der Zielpunkt ${\vec {x}}$ sozusagen in einem Gang (der Breite 0) liegt. Im linearisierenden Kegel kann man dann aus beiden Richtungen des Gangs ankommen, er linearisierte ja die Wände. Wenn die zunächst parallelen Wände in einer Richtung unmittelbar ihre Parallelität verlieren und den Gang zumachen, so dass kein noch so kleiner Schritt in diese Richtung möglich ist, kann man im Tangentenkegel nur aus der offenen Richtung in ${\vec {x}}$ ankommen. Das ist der Unterschied, siehe den ersten pathologischen Fall unten. In der Grafik stimmen Tangentenkegel und Linearisierender Kegel im optimalen Punkt überein und sind rot angedeutet.

Die Anforderungen an die NB stellen sicher, dass im optimalen Punkt der Tangentenkegel und der linearisierende Kegel übereinstimmen und der optimale Punkt nicht isoliert ist. Die Übereinstimmung von linearisierenden Kegel und Tangentialkegel wird manchmal auch als eigene Regularitätsbedingung aufgeführt und Abadie Constraint Qualification genannt. Beispiele für Regularitätsbedingungen sind:

Slater-Bedingung (nur für konvexe Probleme): Es gibt einen Punkt ${\tilde {x}}\in S$ , so dass $g_{i}({\tilde {x}})<0$ für alle $1 \leq i \leq m$ und alle Gleichungsnebenbedingungen in $\tilde x$ erfüllt sind. An dieser Stelle sei erwähnt, dass die Constraint Qualification von Slater im Allgemeinen als die Wichtigste angesehen wird.
Lineare Unabhängigkeit – linear independence constraint qualification (LICQ): Die Gradienten der aktiven Ungleichungsbedingungen und die Gradienten der Gleichungsbedingungen sind linear unabhängig im Punkt $\hat{x}$ .
Mangasarian-Fromovitz – Mangasarian-Fromovitz constraint qualification (MFCQ): Die Gradienten der aktiven Ungleichungsbedingungen und die Gradienten der Gleichungsbedingungen sind positiv-linear unabhängig im Punkt $\hat{x}$ .
Konstanter Rang – constant rank constraint qualification (CRCQ): Für jede Untermenge der Gradienten der Ungleichungsbedingungen, welche aktiv sind, und der Gradienten der Gleichungsbedingungen ist der Rang in der Nähe von $\hat{x}$ konstant.
Konstante positive-lineare Abhängigkeit – constant positive-linear dependence constraint qualification (CPLD): Für jede Untermenge der Gradienten, der Ungleichungsbedingungen, welche aktiv sind, und der Gradienten der Gleichungsbedingungen, und falls eine positive-lineare Abhängigkeit im Punkt $\hat{x}$ vorliegt, dann gibt es eine positiv-lineare Abhängigkeit in der Nähe von $\hat{x}$ .

Man kann zeigen, dass die folgenden beiden Folgerungsstränge gelten

${\mbox{LICQ}}\Rightarrow {\mbox{MFCQ}}\Rightarrow {\mbox{CPLD}}$ und ${\mbox{LICQ}}\Rightarrow {\mbox{CRCQ}}\Rightarrow {\mbox{CPLD}}$ ,

obwohl MFCQ nicht äquivalent zu CRCQ ist. In der Praxis werden schwächere Constraint Qualifications bevorzugt, da diese stärkere Optimalitäts-Bedingungen liefern.

Pathologische Fälle

Die CQ sind dazu da, Zustände wie im Ursprung in folgenden Beispielen von der Betrachtung auszuschließen:

Minimiere $f(x,y):=x$ unter den NB $g_{1}(x,y)=-y\leq 0$ und $g_{2}(x,y)=y-x^{3}\leq 0$ .
Minimiere $f(x):=x\in \mathbb {R}$ unter der NB $g(x)=x^{2}\leq 0$ .
Minimiere $f(x):=\left\{{\begin{array}{lll}-{\sqrt {x}}&\mathrm {falls} &x\geq 0\\\infty &\mathrm {sonst} &\end{array}}\right.$ unter der NB $g(x)=x\leq 0$ .

Optimalitätsbedingungen

Notwendige Bedingung

Karush-Kuhn-Tucker-Bedingungen

→ Hauptartikel: Karush-Kuhn-Tucker-Bedingungen

Die Karush-Kuhn-Tucker-Bedingungen sind ein notwendiges Optimalitätskriterium erster Ordnung und eine Verallgemeinerung der notwendigen Bedingung $\nabla f({\vec {x}})={\vec {0}}$ von Optimierungsproblemen ohne Nebenbedingungen sowie der Lagrange-Multiplikatoren für Optimierungsprobleme unter Gleichungsnebenbedingungen. In Worten bedeutet der Satz von Karush-Kuhn-Tucker ungefähr, dass wenn ${\bar {x}}$ ein zulässiger, regulärer und optimaler Punkt ist, sich der Gradient der Zielfunktion $-\nabla f({\bar {x}})$ als positive Linearkombination der Gradienten der aktiven NB darstellen lässt, siehe auch das Bild oben.

Sei $f:D\rightarrow \mathbb{R}$ die Zielfunktion und die Funktionen $g_{i}:D\rightarrow \mathbb{R}$ mit $1 \leq i \leq m$ und die Funktionen $h_{k}:D\rightarrow \mathbb{R}$ mit $1\leq k\leq l$ sind Nebenbedingungs-Funktionen. Alle vorkommenden Funktionen $f,g_{i},h_{k}$ seien einmal stetig differenzierbar. Es sei ${\bar {x}}\in S$ ein regulärer Punkt, das heißt, eine der Regularitätsanforderung (CQ) von oben ist erfüllt. Falls ${\bar {x}}$ ein lokales Optimum ist, dann existieren Konstanten $\mu _{i}$ und $\nu _{k}$ so dass

$\nabla f({\bar {x}})\pm \sum _{{i=1}}^{m}\mu _{i}\nabla g_{i}({\bar {x}})+\sum _{{k=1}}^{l}\nu _{k}\nabla h_{k}({\bar {x}})=0$ ("+" bei Minimierung, "-" bei Maximierung),

$g_{i}({\bar {x}})\leq 0\,,\;\mu _{i}\geq 0\,,\;\mu _{i}g_{i}({\bar {x}})=0$ für alle $1 \leq i \leq m$ ,

$h_{k}({\bar {x}})=0$ für alle $1\leq k\leq l$ .

Jeder Punkt, in dem diese Bedingungen erfüllt sind, heißt Karush-Kuhn-Tucker-Punkt (kurz: KKT-Punkt).

Ist ${\bar {x}}$ ein Punkt des zulässigen Gebietes in dem keine NB aktiv sind, insbesondere keine Gleichheitsnebenbedingungen $h_{k}(x)=0$ vorliegen, dann sind wegen $g_{i}({\bar {x}})<0$ alle $\mu _{i}=0$ und die obigen Bedingungen reduzieren sich auf die bekannte notwendige Bedingung unrestringierter Probleme $\nabla f({\bar {x}})={\vec {0}}$ .

Fritz-John-Bedingungen

→ Hauptartikel: Fritz-John-Bedingungen

Die Fritz-John-Bedingungen (oder kurz FJ-Bedingungen) sind genau wie die KKT-Bedingungen ein Optimalitätskriterium erster Ordnung. Im Gegensatz zu den KKT-Bedingungen kommen sie ohne Regularitätsbedingungen aus, liefern aber eine schwächere Aussage. Unter Umständen stimmen sie mit den KKT-Bedingungen überein.

Ist ${\bar {x}}$ ein zulässiger Punkt, der lokal Optimal ist, dann existieren $\mu _{i},\nu _{k},{\bar z}$ so dass

${\bar {z}}\nabla f({\bar {x}})\pm \sum _{i=1}^{m}\mu _{i}\nabla g_{i}({\bar {x}})+\sum _{k=1}^{l}\nu _{k}\nabla h_{k}({\bar {x}})=0$ ("+" bei Minimierung, "-" bei Maximierung),

$g_{i}({\bar {x}})\leq 0\,,\;\mu _{i}\geq 0\,,\;\mu _{i}g_{i}({\bar {x}})=0$ für alle $1 \leq i \leq m$ ,

$h_{k}({\bar {x}})=0$ für alle $1\leq k\leq l$ .

und $(\mu ,\nu ,{\bar {z}})$ ungleich dem Nullvektor ist.

Jeder Punkt, in dem diese Bedingungen erfüllt sind, heißt Fritz-John-Punkt oder kurz FJ-Punkt. Die FJ-Bedingungen unterscheiden sich nur durch Einführung des Skalars ${\bar {z}}$ vor dem Gradient der Zielfunktion.

Hinreichende Bedingungen

Ist ${\bar {x}}$ ein KKT-Punkt und die Richtung des steilsten Auf- bzw. Abstiegs schließt mit den Flanken des Tangentenkegels einen Winkel kleiner als 90° ein, dann ist ${\bar {x}}$ ein minimaler bzw. maximaler Punkt. Mathematisch: Gilt

$\nabla f({\bar {x}})\cdot {\vec {d}}>0\;(\mathrm {oder} <0)$ für alle ${\vec {d}}\in T(S,{\bar {x}})\setminus \lbrace {\vec {0}}\rbrace$ ,

dann ist ${\bar {x}}$ ein lokales Minimum (bzw. Maximum). Dies ist ein hinreichendes Optimalitätskriterium erster Ordnung. Ein hinreichendes Optimalitätskriterium zweiter Ordnung für einen KKT-Punkt ${\bar {x}}$ besagt, dass wenn ${\bar {x}}$ ein stationärer Punkt und die Hesse-Matrix der Zielfunktion ist positiv (negativ) definit für alle Vektoren aus dem Tangentenkegel, dann ist ${\bar {x}}$ ein lokales Minimum (bzw. Maximum). Mathematisch:

$\nabla f({\bar {x}})={\vec {0}}$ und ${\vec {d}}\cdot \nabla ^{2}f({\bar {x}}){\vec {d}}>0\;({\mathrm {oder}}<0)$ für alle ${\vec {d}}\in T(S,{\bar {x}})\setminus \lbrace {\vec {0}}\rbrace$ .

Darin ist $T(S,{\vec {x}})$ der Tangentenkegel, siehe Regularitäts-Bedingungen, Tangenten- und Linearisierender Kegel.

Sätze zu den Näherungsverfahren

Im Grenzwert der gegen null gehenden Barriereparameter geht die mit Barrierefunktionen gefundene Lösung in die mit den Lagrange Multiplikatoren gefundene Lösung über.
Im Grenzwert der gegen unendlich gehenden Strafparameter geht die mit Straffunktionen gefundene Lösung in die mit den Lagrange Multiplikatoren gefundene Lösung über.
Im Grenzwert unendlich vieler Iterationen strebt die mit der erweiterten Lagrange Methode gefundene Lösung auch gegen die mit den Lagrange Multiplikatoren gefundene Lösung.

Beispiel

Fläche f(a,b) = a b

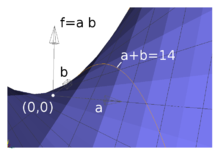
Anhand eines einfachen Beispiels sollen die oben genannten fünf Methoden der Lösung eines Problems erläutert werden. In dem Problem soll das Produkt zweier positiver reeller Zahlen maximiert werden, deren Summe höchsten sechzehn beträgt. Mathematisch formuliert heißt das: Gesucht wird

$f\left(a,b\right)=a\cdot b\rightarrow \mathrm {max}$

mit der NB

$g\left(a,b\right)=a+b-16\leq 0$ .

Es ist anschaulich klar, dass im Optimum die NB aktiv ist, sonst könnte leicht eine bessere Lösung gefunden werden. Der einzige stationäre Punkt mit $\nabla f={\vec {0}}$ dieser in und linearen Funktion liegt in (0,0) weswegen die Suche manchmal in diese Richtung geht. Dann muss man die NB gewissermaßen „in den Weg legen“, damit der Algorithmus sie „bemerkt“.

Eliminierung der Freiheitsgrade

Aus der als aktiv erkannten NB ermittelt man

$a+b-16=0\rightarrow b=16-a$

und die Hilfsfunktion hängt nur noch von ab, so dass die Lösung mittels Kurvendiskussion berechnet werden kann:

${\begin{array}{l}\Pi (a):=f(a,16-a)=a\cdot (16-a)=16a-a^{2}\rightarrow \mathrm {max} \\\rightarrow \Pi '(a)=16-2a=0\rightarrow a=8\rightarrow b=16-8=8\\\rightarrow \Pi ''(a=8)=-2<0\end{array}}$

Man sieht:

Die Hilfsfunktion hat nur noch eine Variable.
Die Lösung ist korrekt, denn es handelt sich um ein Maximum.
Das Verfahren findet vor allem dann Anwendung, wenn bekannt ist, dass die NB aktiv ist, z.B. im Kontakt fest verklebter Bauteile.

Lagrange-Multiplikator

Hier wird die $\lambda$ -fache NB von der Zielfunktion subtrahiert, worin der Faktor $\lambda$ der Lagrange-Multiplikator ist und wie eine zusätzliche Unbekannte behandelt wird. Die Subtraktion wird gewählt, damit eine Verletzung der NB bei $\lambda >0$ bestraft wird. Die Hilfs- oder Lagrange-Funktion lautet hier also:

$\Pi (a,b,\lambda )=a\cdot b-\lambda (a+b-16)\rightarrow \mathrm {max}$ .

Im Minimum verschwinden alle Ableitungen nach allen Variablen:

${\begin{aligned}{\frac {\partial \Pi }{\partial a}}=&b-\lambda =0&\rightarrow \lambda &=b\\{\frac {\partial \Pi }{\partial b}}=&a-\lambda =0&\rightarrow a&=\lambda =b\\{\frac {\partial \Pi }{\partial \lambda }}=&16-a-b=16-2a=0&\rightarrow a&=b=\lambda =8\end{aligned}}$

und die Lösung $a=b=8$ ist gefunden. Wegen $g(a=8,b=8)=0$ und $\lambda =8\geq 0$ ist die Karush-Kuhn-Tucker-Bedingung erfüllt. Das obige Gleichungssystem kann als Matrizengleichung geschrieben werden:

${\begin{pmatrix}1&0&-1\\0&1&-1\\-1&-1&0\end{pmatrix}}{\begin{pmatrix}b\\a\\\lambda \end{pmatrix}}={\begin{pmatrix}0\\0\\-16\end{pmatrix}}$

Die Methode der lagrangeschen Multiplikatoren

erfüllt die NB exakt,
führt zusätzliche Unbekannte ( $\lambda$ ) ein,
schleust verschwindende Diagonalelemente in das Gleichungssystem ein, die bei Anwendung der Cholesky-Zerlegung problematisch sind.
kann anhand des Vorzeichens von $\lambda$ beurteilen, ob die Nebenbedingung aktiv ist oder nicht (positiv bei Aktivität).

Barrierefunktion

Mit Barrierefunktionen können Neben-Bedingungen mit Sicherheit erfüllt werden zu dem Preis, dass im Optimum die NB nicht ausgereizt wird. Bei der Suche nach einer Lösung wird zur Ziel-Funktion das -fache einer Barrierefunktion hinzu addiert, z.B.:

$\Pi \left(a,b\right)=a{\cdot }b+2r\ln(16-a-b)\rightarrow \mathrm {max}$ .

Darin ist $\ln(16-a-b)$ eine logarithmische Barrierefunktion und der Barriereparameter. Im Extremum verschwinden wieder alle Ableitungen:

${\begin{aligned}{\frac {{\partial }\Pi }{\partial a}}=b-{\frac {2r}{16-a-b}}=0\\{\frac {{\partial }\Pi }{\partial b}}=a-{\frac {2r}{16-a-b}}=0\end{aligned}}$ ,

und daher a=b sowie $a(16-2a)-2r=-2(a^{2}-8a+r)=0$ , was die Lösung

$a=b=4\pm {\sqrt {16-r}}\leq 8$

besitzt, die für $r\rightarrow 0$ die Lösungen $(a,b)\in \{(0,0),(8,8)\}$ annimmt. Bei der iterativen Suche mit dem Newton-Raphson Verfahren bekommt man die Vorschrift

${\nabla }\Pi +\nabla ^{2}\Pi \Delta {\vec {x}}={\begin{pmatrix}b-{\frac {2r}{16-a-b}}\\a-{\frac {2r}{16-a-b}}\end{pmatrix}}+{\begin{pmatrix}-{\frac {2r}{(16-a-b)^{2}}}&1-{\frac {2r}{(16-a-b)^{2}}}\\1-{\frac {2r}{(16-a-b)^{2}}}&-{\frac {2r}{(16-a-b)^{2}}}\end{pmatrix}}{\begin{pmatrix}\Delta a\\\Delta b\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}$

für die Berechnung des Inkrements $\Delta a$ und $\Delta b$ . Die Determinante der Hesse-Matrix ${\nabla }^{2}\Pi$ lautet:

${\frac {4r^{2}}{(16-a-b)^{4}}}-\left(1-{\frac {2r}{(16-a-b)^{2}}}\right)^{2}={\frac {4r}{(16-a-b)^{2}}}-1$ .

Man sieht:

Die Nebenbedingung wird eingehalten.
Im Grenzwert $r\rightarrow 0$ erhält man die exakte Lösung.
Für $r>16$ existiert kein optimaler Punkt. Allgemein stimmen die Höhenlinien der Hilfsfunktion nicht mit denen der Zielfunktion überein.
Bei Annäherung an die Lösung und mit $r\rightarrow 0$ kann die Hesse-Matrix schlecht konditioniert sein.
Bei einer inkrementellen Suche muss sichergestellt werden, dass das Inkrement in den Unbekannten nicht so groß ist, dass man aus Versehen auf der falschen Seite der Barriere landet, wo die Barrierefunktion in diesem Beispiel nicht definiert ist.

Strafverfahren

Mit Straf-Verfahren können Neben-Bedingungen näherungsweise erfüllt werden. Bei der Suche nach einer Lösung wird von der Ziel-Funktion das -fache einer Straffunktion abgezogen (soll ja die Verletzung bestrafen):

$\Pi (a,b)=a\cdot b-{\frac {r}{n}}\cdot \mathrm {max} (0,a+b-16)^{n}\rightarrow \mathrm {max}$ .

Darin ist der Straf-Parameter und $\mathrm {max} (0,a+b-16)^{n}$ die Straffunktion. Mit n=1 nennt man die Straffunktion exakt, sie ist aber nicht differenzierbar. Hier soll n=2 benutzt werden. Im Extremum verschwinden wieder alle Ableitungen:

${\begin{aligned}{\frac {\partial \Pi }{\partial a}}=b-r\cdot \mathrm {max} (0,a+b-16)=0\\{\frac {\partial \Pi }{\partial b}}=a-r\cdot \mathrm {max} (0,a+b-16)=0\end{aligned}}$ .

Mit $a+b-16\leq 0$ bekommt man a=b=0 weswegen man hier im „verbotenen“ Gebiet $a+b-16>0$ starten muss. Dann folgt aus

${\begin{aligned}{\frac {\partial \Pi }{\partial a}}=&b-r(a+b-16)=0&\rightarrow \quad a+\left(1-{\frac {1}{r}}\right)b=&16\\{\frac {\partial \Pi }{\partial b}}=&a-r(a+b-16)=0&\rightarrow \quad \left(1-{\frac {1}{r}}\right)a+b=&16\end{aligned}}$

das Gleichungssystem

${\begin{pmatrix}1-{\frac {1}{r}}&1\\1&1-{\frac {1}{r}}\end{pmatrix}}{\begin{pmatrix}a\\b\end{pmatrix}}={\begin{pmatrix}16\\16\end{pmatrix}}$

mit der Lösung

$a=b={\frac {16r}{2r-1}}=8+{\frac {8}{2r-1}}>8$ ,

die für $r\rightarrow \infty$ in die Lösung $a=b=8$ übergeht.

Man sieht:

Die Nebenbedingung wird nur näherungsweise erfüllt aber mit wachsendem Strafparameter immer besser, allerdings nur weil hier exakt gerechnet werden kann. Bei numerischer Lösung des Gleichungssystems würden Rundungsfehler mit wachsendem Strafparameter zu Fehlern führen.
Der Grund hierfür liegt darin, dass mit zunehmendem Strafparameter der Wert der Determinante des Gleichungssystems $\left(1-{\frac {1}{r}}\right)^{2}-1={\frac {1}{{r}^{2}}}-{\frac {2}{r}}$ gegen null geht. Das Problem ist zunehmend schlecht gestellt.
Es muss ein Kompromiss hinsichtlich der Konditionierung des Gleichungssystems und der Genauigkeit der Erfüllung der NB gefunden werden.
Durch Einsetzen von und in die NB kann geprüft werden, wie stark sie verletzt wird.
Es werden keine zusätzlichen Variablen oder verschwindende Diagonalelemente eingeschleust, es existiert eine Lösung für alle Strafparameter $r\neq 1/2$ und das Verfahren gilt als numerisch robust.

Erweiterte oder verallgemeinerte-Lagrange-Methode

Die erweiterte oder verallgemeinerte Lagrange-Methode (englisch augmented-lagrange-method) benutzt die Straffunktion, um die Lagrange-Multiplikatoren näherungsweise zu berechnen. Bei der Suche nach einer Lösung wird von der Zielfunktion das $\lambda _{i}$ -fache der NB und das -fache einer Straffunktion abgezogen (Strafidee):

$\Pi (a,b)=a\cdot b-{\frac {1}{2r}}\left(\mathrm {max} (0,\lambda _{i}+r(a+b-16))^{2}-\lambda _{i}^{2}\right)\rightarrow \mathrm {max}$ .

Im Extremum verschwinden alle Ableitungen:

${\begin{aligned}{\frac {\partial \Pi (a,b)}{\partial a}}=b-\mathrm {max} (0,\lambda _{i}+r(a+b-16))=0\\{\frac {\partial \Pi (a,b)}{\partial b}}=a-\mathrm {max} (0,\lambda _{i}+r(a+b-16))=0\end{aligned}}$ .

Mit $\lambda _{i}+r(a+b-16)\leq 0$ bekommt man a=b=0 . Andernfalls entsteht aus

${\begin{aligned}b-\lambda _{i}-r(a+b-16)=&0&\rightarrow \quad a+\left(1-{\frac {1}{r}}\right)b=16-{\frac {\lambda _{i}}{r}}\\a-\lambda _{i}-r(a+b-16)=&0&\rightarrow \quad \left(1-{\frac {1}{r}}\right)a+b=16-{\frac {\lambda _{i}}{r}}\end{aligned}}$

das Gleichungssystem

${\begin{pmatrix}1-{\frac {1}{r}}&1\\1&1-{\frac {1}{r}}\end{pmatrix}}{\begin{pmatrix}a\\b\end{pmatrix}}={\begin{pmatrix}16-{\frac {\lambda _{i}}{r}}\\16-{\frac {\lambda _{i}}{r}}\end{pmatrix}}$ ,

das die Lösung

$a_{i+1}=b_{i+1}={\frac {16r-\lambda _{i}}{2r-1}}=8+{\frac {8-\lambda _{i}}{2r-1}}$

hat.

Die numerische Suche des Extremums mit der erweiterten Lagrange-Methode

startet normalerweise mit und den Anfangswerten $a_{0}=b_{0}=\lambda _{0}=0$ ,
berechnet $a_{{i+1}}$ und $b_{i+1}$ (im nicht-linearen Fall Iteration bis zur Konvergenz),
setzt $\lambda _{i+1}=\mathrm {max} (0,\lambda _{i}+r\cdot g(a_{i+1},b_{i+1}))=\mathrm {max} (0,\lambda _{i}+r\cdot (a_{i+1}+b_{i+1}-16))$ und
bricht ab, wenn ein geeignetes Konvergenzkriterium erfüllt ist oder inkrementiert und kehrt in Schritt 2 zurück.

Hier muss allerdings ein Startwert mit $a+b-16>0$ vorgegeben werden, damit der Punkt $(a,b)=(8,8)$ gefunden werden kann. Mit $r=100\,,\;a_{0}=100$ und $b_{0}=\lambda _{0}=0$ ergibt sich bis zu einem Fehler $|a_{i}-a_{i-1}|<10^{-10}$ folgender Iterationsverlauf:

	$a_{i}$	$a_{i}-a_{{i-1}}$	$\lambda _{i}$	$a_{i}b_{i}-a_{i-1}b_{i-1}$	$a_{i}+b_{i}-16$
1	8.04020100503	−91.959798995	8.04020100502	64.6448322012	0.0804020100502
2	7.9997979849	−0.0404030201258	7.9997979849	−0.648064402007	−0.000404030201256
3	8.00000101515	0.000203030251889	8.00000101515	0.00324844322116	2.03030252166e-06
4	7.9999999949	−1.02025252513e-06	7.9999999949	−1.63240414395e-05	−1.02025285997e-08
5	8.00000000003	5.12689890542e-09	8.00000000003	8.20303824867e-08	5.12692110988e-11
6	8.0	−2.57633914202e-11	8.0	−4.12214262724e-10	−2.57571741713e-13

Mit einem größeren Straf-Parameter wäre die Konvergenz schneller, das Beispiel aber weniger illustrativ.

Die erweiterte Lagrange-Methode

erfüllt die NB beliebig genau,
führt weder neue Unbekannte ein noch beeinträchtigt sie die Konditionierung des Gleichungssystems,
benötigt dazu mehrere konvergierte Lösungen des globalen Problems (im zweiten Schritt) und
kann die Aktivität der Neben-Bedingung an $\lambda _{i}$ messen.

Literatur

R. Reinhardt, A. Hoffmann, T. Gerlach: Nichtlineare Optimierung. Springer, 2013, ISBN 978-3-8274-2948-3.

Basierend auf einem Artikel in:

Wikipedia.de