Maßproblem

Das Maßproblem ist ein Problem in der Mathematik, das grundlegend für die Maßtheorie ist. Es stellt die Frage, ob man jeder Teilmenge der Ebene, das heißt jeder in beliebiger Weise aus Punkten der Ebene zusammengesetzten Menge, in vernünftiger Weise ein Flächenmaß, oft auch Flächeninhalt genannt, zuordnen kann. Abhängig davon, was als vernünftig gelten soll, lautet die überraschende Antwort nein. Nicht nur in der zweidimensionalen Ebene, sondern auch in anderen Dimensionen ist die entsprechende Fragestellung negativ zu beantworten.

Das Maßproblem in der Ebene

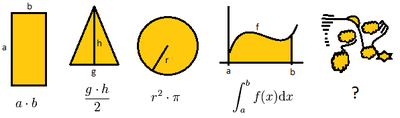
Komplexer werdende Teilmengen der Ebene und ihre Flächeninhalte

Schon in der elementaren Schulmathematik lernt man, gewissen Teilmengen der Ebene, die man Flächen nennt, Zahlen als ihren Flächeninhalt zuzuordnen. Ein Rechteck erhält den Flächeninhalt „Seite mal Seite“, einem Dreieck wird „Grundseite mal Höhe durch 2“ zugeordnet. Später kommen krummlinig berandete Flächen wie Kreise ( $\pi$ mal Radius zum Quadrat) hinzu, noch später werden Flächenstücke unter Kurven betrachtet, die Methoden zur Ermittlung des Flächeninhalts werden dabei zunehmend komplexer. Kann man das immer weiter treiben und schließlich jeder Teilmenge der Ebene in vernünftiger Weise eine Zahl als Flächeninhalt zuordnen?

An ein vernünftiges Flächenmaß, das jeder Menge $A\subset \mathbb {R} ^{2}$ , also jeder Teilmenge der Ebene, eine Zahl $\mu (A)$ als Flächeninhalt zuordnet, wird man folgende Forderungen stellen (der griechische Buchstabe μ soll dabei an Maß erinnern):

Positivität: Für jede Menge $A\subset {\mathbb R}^2$ ist $\mu(A) \ge 0$ , wobei auch $\infty$ zugelassen ist. Negative Zahlen werden nicht als Flächeninhalte zugelassen.

Kongruenz: Sind zwei Mengen $A,B\subset \mathbb {R} ^{2}$ kongruent, d. h. sie gehen durch Parallelverschiebung, Spiegelung oder Drehung auseinander hervor, so sollen sie dasselbe Flächenmaß haben, d.h., es soll $\mu(A)=\mu(B)$ gelten.

Normiertheit: Das Einheitsquadrat $[0,1]^{2}\subset \mathbb {R} ^{2}$ soll das Flächenmaß 1 haben, d. h. $\mu \left([0,1]^{2}\right)=1$ . Damit ist die einfache, aber wenig sinnvolle Lösung, alle Flächeninhalte auf 0 festzulegen, ausgeschlossen.

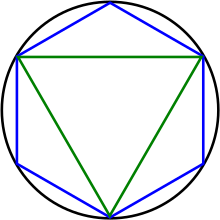
Ausschöpfung eines Kreises durch Dreiecke

Für die nächste Eigenschaft erinnern wir uns daran, wie man einen Kreis durch eine Folge immer kleiner werdender Dreiecke ausschöpfen kann. Man beginnt damit, dem Kreis ein gleichseitiges Dreieck einzubeschreiben. Anschließend setzt man auf jede Dreiecksseite ein gleichschenkliges Dreieck, dessen Spitze auf der Kreislinie liegt und dessen Grundseite nicht dazugehören soll, und erhält so ein dem Kreis einbeschriebenes Sechseck. Indem man dies wiederholt, erhält man ein Zwölfeck, dann ein 24-Eck usw. Man sieht, dass sich der Kreis aus unendlich vielen nicht überlappenden Dreiecken zusammensetzt. Der Flächeninhalt des Kreises berechnet sich dann als die „unendliche Summe“ der immer kleiner werdenden Dreiecke. Damit solche Konstruktionen erfolgreich sein können, muss man an das Flächenmaß noch folgende Anforderung stellen:

$\sigma$ -Additivität: Ist $A_{1},A_{2},A_{3},\ldots \subset \mathbb {R} ^{2}$ eine Folge von paarweise punktfremden Mengen, d. h. $A_i \cap A_j = \emptyset$ für $i\neq j$ , so soll die unendliche Vereinigung $A_1\cup A_2\cup A_3\cup\ldots$ die Reihe $\mu(A_1) + \mu(A_2) + \mu(A_3) + \ldots$ als Flächenmaß haben, d. h. in kompakter Schreibweise: $\mu \left(\bigcup _{i=1}^{\infty }A_{i}\right)=\sum _{i=1}^{\infty }\mu (A_{i})$ , falls $A_i \cap A_j = \emptyset$ für alle $i\neq j$ .

Das $\sigma$ in der Bezeichnung $\sigma$ -Additivität soll darauf hinweisen, dass hier abzählbar unendliche Summen behandelt werden.

Bezeichnet man die Menge aller Teilmengen von $\mathbb {R} ^{2}$ wie üblich mit ${\mathcal {P}}\left(\mathbb {R} ^{2}\right)$ , so lautet das Maßproblem in seiner präzisen Form:

Gibt es eine Abbildung $\mu \colon {\mathcal {P}}\left(\mathbb {R} ^{2}\right)\rightarrow [0,\infty ]$ , die die oben genannten Eigenschaften Positivität, Kongruenz, Normiertheit und $\sigma$ -Additivität erfüllt?

Das Maßproblem in n Dimensionen

Das Maßproblem kann leicht auf -dimensionale Räume ausgedehnt werden; das umfasst die der Anschauung zugänglichen Dimensionen 1, 2 und 3, wobei man es dann mit Längen-, Flächen- bzw. Volumenmessung zu tun hat. Das Maßproblem in Dimensionen lautet:

Gibt es eine Abbildung $\mu _{n}:{\mathcal {P}}\left(\mathbb {R} ^{n}\right)\rightarrow [0,\infty ]$ mit folgenden Eigenschaften:

Positivität: $\mu_n(A)\ge 0$ für alle $A\subset \mathbb {R} ^{n}$ (diese Bedingung steckt eigentlich bereits in der Vorgabe des Bildbereichs der Abbildung),
Kongruenz: $\mu _{n}(A)=\mu _{n}(B)$ , falls A und B kongruent sind,
Normiertheit: $\mu _{n}\left([0,1]^{n}\right)=1$ ,
$\sigma$ -Additivität: $\mu _{n}\left(\bigcup _{i=1}^{\infty }A_{i}\right)=\sum _{i=1}^{\infty }\mu _{n}\left(A_{i}\right)$ , falls $A_i \cap A_j = \emptyset$ für alle $i\neq j$ ?

Man könnte sogar noch weitere naheliegende Forderungen an eine Maßfunktion stellen:

Leere Menge: $\mu _{n}(\emptyset )=0$ ,

Einpunktmenge: $\mu _{n}\left(\{x\}\right)=0$ für alle Punkte $x\in \mathbb {R} ^{n}$ ,

Additivität: $\mu _{n}(A_{1}\cup A_{2})=\mu _{n}(A_{1})+\mu _{n}(A_{2})$ , falls $A_1 \cap A_2 = \emptyset$ , oder

Monotonie: $\mu_n(A) \le \mu_n(B)$ , falls $A\subset B$ .

Diese Eigenschaften können leicht als einfache Konsequenzen der eingangs formulierten Eigenschaften erkannt werden, sie stellen also keine weitergehenden Forderungen dar.

Unlösbarkeit des Maßproblems

Hier wird mittels einer auf den italienischen Mathematiker Giuseppe Vitali zurückgehenden Idee gezeigt, dass das Maßproblem für den eindimensionalen Fall ${\mathbb R}^1 = {\mathbb R}$ nicht lösbar ist. Dazu konstruiert man eine Menge $V\subset[0,1]$ , die sogenannte Vitali-Menge, mit folgenden Eigenschaften:

Sind und verschiedene rationale Zahlen, so ist $(p+V) \cap (q+V)=\emptyset$ . Dabei ist die um verschobene Menge.
Ist die Folge $(p_n)_{n\in{\mathbb N}}$ eine Abzählung der im Intervall enthaltenen rationalen Zahlen, so ist $\textstyle [0,1]\subset\bigcup_{n=1}^\infty p_n+V$ .

Daraus ergibt sich nun leicht die Unlösbarkeit des Maßproblems. Wäre nämlich $\mu$ eine Lösung, so wäre wegen der zweiten Eigenschaft und weil jedes p_n+V im Intervall [-1,2] liegt:

$[0,1] \subset\bigcup_{n=1}^\infty p_n+V \subset [-1,2].$

Da $[-1,2] = [-1,0)\cup [0,1] \cup (1,2]$ überlegt man sich leicht, dass $\mu([-1,2])=3$ sein muss. Aus der Monotonie ergibt sich daher

$1\leq \mu \left(\bigcup _{n=1}^{\infty }p_{n}+V\right)\leq 3.$

Nach der ersten Eigenschaft sind die Mengen p_n+V paarweise disjunkt, so dass aus der $\sigma$ -Additivität

$1 \le \sum_{n=1}^\infty \mu(p_n+V) \le 3$

folgt. Nun sind die Mengen p_n+V alle kongruent, denn sie gehen durch Verschiebungen auseinander hervor. Daher sind die Zahlen $\mu(p_n+V)$ alle gleich. Dann kann die unendliche Summe aber nur 0 oder $\infty$ sein, sie kann jedenfalls nicht zwischen 1 und 3 liegen. Dieser Widerspruch zeigt, dass das Maßproblem nicht lösbar ist.

Es bleibt noch die Aufgabe, die Menge anzugeben: $\mathbb{Q} \subset \R$ ist eine Untergruppe. Jede Nebenklasse von $\mathbb {Q}$ enthält Elemente aus [0,1] . Mit Hilfe des Auswahlaxioms wählen wir aus jeder Nebenklasse von $\mathbb {Q}$ ein solches Element und fassen diese zur Menge zusammen. Dann ist in [0,1] enthalten, und man überlegt sich leicht, dass auch die beiden genannten Eigenschaften hat. Die erste Eigenschaft gilt, da aus jeder Nebenklasse genau ein Element enthält. Zum Nachweis der zweiten Eigenschaft sei $x\in [0,1]$ beliebig. Dieses muss in irgendeiner Nebenklasse liegen, denn die Vereinigung über alle Nebenklassen ist $\mathbb {R}$ . Da aus jeder Nebenklasse ein Element enthält, gibt es ein $v\in V$ , das in derselben Nebenklasse wie liegt, für dieses gilt daher $x-v\in \mathbb{Q}$ . Da und beide zwischen 0 und 1 liegen, ist auch $x-v\in[-1,1]$ , d.h. es gibt ein mit $x-v\,=\,p_m$ . Dann folgt $\textstyle x=p_m+v\in p_m+V \subset \bigcup_{n=1}^\infty p_n+V$ , was den Beweis beendet.

Damit ist die Unlösbarkeit des Maßproblems für ${\mathbb R}^1$ vollständig gezeigt. Daraus ergibt sich sofort auch die Unlösbarkeit in höheren Dimensionen, denn wäre $\mu _{n}$ eine Lösung des Maßproblems für die Dimension , so wäre durch

$\mu_1(A):=\mu_n(A\times [0,1]^{n-1})$

eine Lösung des eindimensionalen Falls gegeben, von deren Nichtexistenz wir uns aber gerade überzeugt haben.

Historische Bemerkungen

Mathematiker vergangener Tage waren mit Begriffen wie Flächeninhalt oder Volumen recht sorglos umgegangen. Erst durch die cantorsche Mengenlehre und die damit einhergehende strengere Formalisierung der Mathematik konnten solche Probleme überhaupt erkannt und formuliert werden. Die älteste Formulierung des Maßproblems geht auf Henri Léon Lebesgue zurück. In seiner 1902 eingereichten Dissertation weist er darauf hin, es nicht allgemein lösen zu können, sondern nur für eine bestimmte Klasse von Mengen, die er messbar nannte. Bereits 1904 konnte Giuseppe Vitali die Unlösbarkeit des Maßproblems zeigen.

Die Messung der Größe einer Menge (Länge, Flächeninhalt, Volumen) ist aber eine der wesentlichen Aufgabenstellungen in der Mathematik, was nicht nur für Anwendungen, sondern auch für viele mathematische Theorien von fundamentaler Bedeutung ist. Ein Ausweg aus diesem Dilemma könnte darin bestehen, die Forderungen an das Maß abzuschwächen. Das hat Felix Hausdorff 1914 getan, indem er die $\sigma$ -Additivität durch die schwächere Forderung der Additivität ersetzte. Man spricht dann nicht von einem Maß, sondern von einem Inhalt. Es ist klar, dass Vitalis Argumentation für Inhalte zusammenbricht, und Felix Hausdorff konnte tatsächlich zeigen, dass es in den Dimensionen 1 und 2 Inhalte gibt, aber für $n\ge 3$ gibt es diese auch nicht mehr.

Als sehr viel erfolgreicher hat sich ein anderer Ausweg erwiesen. Man behält die stärkere und für viele Beweise wichtige technische Forderung der $\sigma$ -Additivität bei und verkleinert den Bereich der Mengen, denen man ein Maß zuordnet, wie es Lebesgue bereits in seiner Doktorarbeit getan hat. Daraus sind die Maßtheorie und die lebesguesche Integrationstheorie hervorgegangen. Felix Hausdorff schreibt 1914 in seinem Buch Grundzüge der Mengenlehre dazu:

Die Theorie des Inhalts hat sich in zwei Stufen entwickelt, die man am besten durch zwei Gesetze für additives Verhalten charakterisiert. Der Inhaltsbegriff der älteren Stufe, auf Ansätzen von G. Cantor und H. Hankel beruhend und von G. Peano und C. Jordan vervollständigt, erfüllt die Gleichung

$f(A+B)\,=\,f(A)+f(B)$

für zwei (oder endlich viele) paarweise fremde Mengen; der Inhaltsbegriff der neueren Stufe, den wir E. Borel und H. Lebesgue verdanken, erfüllt die Gleichung

$f(A+B+C+\cdots)=f(A)+f(B)+f(C)+\cdots$

für eine endliche oder abzählbare Menge von Summanden. Der älteren Stufe entspricht der Riemannsche, der neuen der Lebesguesche Integralbegriff. Der Übergang vom Endlichen zum Abzählbaren darf als einer der größten Fortschritte in der Mathematik bezeichnet werden ...

Man beschränkt sich also auf die sogenannten Lebesgue-messbaren Mengen. Vitalis Argument zeigt dann, dass die oben angegebene Menge V nicht Lebesgue-messbar sein kann, was auch als Satz von Vitali bekannt ist. Das Verfahren zur Gewinnung dieser Menge V ist nicht konstruktiv, da das Auswahlaxiom verwendet wurde. Die Frage, ob die Verwendung des Auswahlaxioms (oder einer schwächeren Variante dieses Axioms) zwingend ist, wurde 1970 von Robert M. Solovay mit ja beantwortet, indem er ein Modell der Mengenlehre angab, in dem das Auswahlaxiom nicht gilt und in dem jede Teilmenge von $\mathbb {R}$ messbar ist.

Basierend auf einem Artikel in:

Wikipedia.de