
Analytische Fortsetzung
In der Analysis versteht man unter
der analytischen Fortsetzung einer Funktion, die auf einer Teilmenge
der reellen oder komplexen Zahlen definiert ist, eine analytische
Funktion, die auf einem komplexen Gebiet,
das
umfasst, definiert ist und auf der Teilmenge
mit der ursprünglichen Funktion übereinstimmt. Hier sind fast ausschließlich die
Fälle von Interesse, in denen die Fortsetzung (und in der Regel auch ein
maximales Gebiet) durch die vorgegebene Menge
und die auf ihr definierte Funktion
eindeutig bestimmt ist.
In der Funktionentheorie, insbesondere bei Untersuchungen von Funktionen in mehreren komplexen Variablen, wird der Begriff abstrakter gefasst. Hier bedeutet analytische Fortsetzung das Fortsetzen einer holomorphen Funktion bzw. eines holomorphen Funktionskeims. Dabei wird unterschieden zwischen der Fortsetzung des Keimes entlang eines Weges und der Fortsetzung zu einer Funktion auf einem Gebiet.
Bedeutungsvoll ist, dass holomorphe Funktionen – anders als etwa stetige oder lediglich beliebig oft differenzierbare Funktionen – bereits aus lokalen Daten auf einer sehr kleinen Umgebung sehr gut rekonstruiert werden können.
Analytische Fortsetzung in der Analysis
Für die elementare Analysis wichtige Aussagen über Fortsetzbarkeit sind die folgenden:
- Sei
ein reelles (offenes oder abgeschlossenes) Intervall. Dann ist eine Funktion
genau dann analytisch fortsetzbar,
-
- wenn für jeden Punkt des Intervalls eine offene Umgebung existiert, auf der sich die Funktion durch eine absolut konvergente Potenzreihe darstellen lässt, oder
- wenn
in jedem Punkt des Intervalls beliebig oft differenzierbar ist und die Taylorreihe zu jedem Punkt des Intervalls einen nicht verschwindenden Konvergenzradius hat.
- In beiden Fällen liefern die genannten Reihen – theoretisch nur lokal, in
vielen praktisch wichtigen Fällen aber bei geeigneter Wahl des
Entwicklungspunktes auf einem komplexen Gebiet, das das gesamte Intervall
umfasst – eine Beschreibung der hier eindeutig bestimmten analytischen Fortsetzung als Potenzreihe.
- Wenn die abgeschlossene
Hülle einer unendlichen Menge
zusammenhängend, also zum Beispiel ein reelles Intervall ist und eine analytische Fortsetzung
von
auf ein Gebiet
existiert, dann stimmt eine zweite auf
holomorphe Funktion
bereits dann mit der Fortsetzung
überein,
-
- wenn sie mit
auf einer unendlichen Teilmenge von
, die sich in
häuft, übereinstimmt oder
- wenn in irgendeinem festen Punkt von
die Funktionswerte und alle Ableitungen von
und
übereinstimmen.
- wenn sie mit
Die hier genannten und einige andere Sätze über die analytische Fortsetzbarkeit und die Eindeutigkeit der Fortsetzung sind in den nachfolgenden, abstrakteren Formulierungen der Funktionentheorie als Spezialfälle enthalten.
Beispiele
- Jede ganzrationale
Funktion auf
, also jede reelle Funktion, deren Funktionsterm ein Polynom in
ist, lässt sich auf
analytisch durch die Funktion mit dem gleichen Funktionsterm fortsetzen.
- Die gebrochenrationale
Funktion
lässt sich auf das Gebiet
fortsetzen. Im Inneren des Einheitskreises
kann die Fortsetzung durch die Potenzreihe
dargestellt werden, im Äußeren
durch die Laurentreihe
. Beide Fortsetzungen
lassen sich lokal über ihr Konvergenzgebiet hinaus durch Potenzreihen analytisch fortsetzen. Sie lassen sich also zu einer gemeinsamen analytischen Fortsetzung auf
zusammensetzen, dies ist, wie immer bei gebrochenrationalen reellen Funktionen natürlich die komplexe gebrochenrationale Funktion
.
- Die reellen Exponentialfunktionen,
die Sinus-Funktion
und die Cosinus-Funktion
lassen sich als Potenzreihen mit dem Konvergenzradius
darstellen. Daher kann man sie analytisch zu ganzen Funktionen fortsetzen, die dann durch die gleichen Potenzreihen darstellbar sind.
- Die auf
definierte Fakultätsfunktion
besitzt als analytische Fortsetzung die Gammafunktion
diese Fortsetzung wird allerdings erst durch die zusätzliche Bedingung eindeutig, dass die Fortsetzung logarithmisch konvex sein soll. → Siehe Satz von Bohr-Mollerup.
Keim
Um eine präzise Definition einer analytischen Fortsetzung im Sinne der
Funktionentheorie zu geben, müssen zuerst die Begriffe Halm und
Funktionskeim erläutert werden: Sei
eine komplexe
Mannigfaltigkeit und
ein Punkt. Zudem seien
zwei Umgebungen von
und
zwei holomorphe
Funktionen. Die beiden Funktionen heißen äquivalent im Punkt
,
falls eine Umgebung
von
existiert mit
.
Die Menge all dieser Äquivalenzklassen wird als Halm
bezeichnet, die Äquivalenzklassen als (Funktions-)Keime. Die Projektion einer
Funktion
auf ihren Keim im Punkt
wird mit
notiert.
Anschaulich beschreibt der Keim
einer Funktion das Verhalten von
in „unmittelbarer“ Umgebung von
.
Das ist mehr als der bloße Funktionswert
,
denn auch die Ableitungen
usw. lassen sich aus dem Keim ablesen, da sie sich aus jeder noch so kleinen
Umgebung von
ergeben.
Der Halm
trägt auf natürliche Weise die Struktur einer
-Algebra.
Er ist isomorph zur
-Algebra
der in
konvergenten Potenzreihen,
da das lokale Verhalten einer holomorphen Funktion durch ihre
Potenzreihenentwicklung eindeutig bestimmt ist.
Fortsetzung entlang eines Weges
Sei
eine zusammenhängende komplexe Mannigfaltigkeit,
zwei Punkte und
sowie
zwei Funktionskeime.
heißt analytische Fortsetzung von
entlang des Weges
mit
,
falls folgendes gilt: Es existieren Punkte
mit offenen Umgebungen
und holomorphen Funktionen
derart, dass
für
Mit anderen Worten: Es gibt eine endliche Folge von offenen Umgebungen,
welche die Kurve überdecken. Auf diesen Umgebungen sind jeweils holomorphe
Funktionen definiert, welche in den Bereichen übereinstimmen, wo sich die
Umgebungen überlappen. Häufig wählt man offene Kreise als Mengen ,
denn diese treten als Konvergenzbereiche von Reihenentwicklungen auf; in diesem
Fall spricht man von einer Kreiskette.
Diese Fortsetzung hängt im Allgemeinen von der Wahl des Weges ab (nicht
jedoch von den Zwischenpunkten
und den Umgebungen
).
Auch gibt es im Allgemeinen keine in einer Umgebung
von ganz
holomorphe Funktion
mit
und
.
Definition
Sei
eine zusammenhängende
komplexe Mannigfaltigkeit,
ein Punkt und
ein Funktionskeim. Das Quadrupel
heißt eine analytische Fortsetzung von
,
falls gilt:
ist eine zusammenhängende komplexe Mannigfaltigkeit.
ist eine holomorphe Abbildung und ein lokaler Homöomorphismus.
ist eine holomorphe Funktion.
so, dass
und
, wobei
die Projektion von
auf die Äquivalenzklasse ihres Keims in
bezeichnet.
Die auf diese Weise definierte analytische Fortsetzung hängt mit der
Fortsetzung entlang eines Weges zusammen: Wenn
ein Weg mit Anfangspunkt
und Endpunkt
ist, dann ist
ein Weg mit Anfangspunkt
und Endpunkt
.
Die Funktion
definiert in einer Umgebung von
durch
einen Funktionskeim in
.
Beispiel
und sei
der Keim in
desjenigen Zweiges der holomorphen Quadratwurzel mit
.
Analytische Fortsetzungen davon beispielsweise sind:
- Die durch die Taylorreihe
um
in der offenen Kreisscheibe
definierte Funktion
. Die Projektion
ist die natürliche Inklusionsabbildung.
- Der Hauptzweig der Quadratwurzel, definiert auf der geschlitzten komplexen
Ebene
, wobei
wieder die natürliche Inklusionsabbildung ist.
Alle Beispiele haben gemeinsam, dass
als Teilmenge von
aufgefasst werden kann. Die beiden letzten Beispiele zeigen zudem, dass es
innerhalb von
kein größtes Gebiet gibt, auf dem die Funktion holomorph fortgesetzt werden
kann. Die Frage nach der größtmöglichen Fortsetzung führt zur Definition der
maximalen analytischen Fortsetzung:
Maximale Analytische Fortsetzung
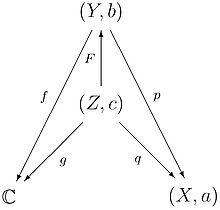
Sei
eine zusammenhängende komplexe Mannigfaltigkeit,
ein Punkt und
ein Funktionskeim. Eine analytische Fortsetzung
von
heißt maximale analytische Fortsetzung, falls für jede andere analytische
Fortsetzung
von
gilt: Es existiert eine holomorphe Abbildung
mit
,
und
.
Existenz und Eindeutigkeit
Direkt aus der Definition folgt die Eindeutigkeit der maximalen analytischen
Fortsetzung bis auf holomorphe Isomorphie. Die Existenz kann mit Hilfe der Garbentheorie
gezeigt werden:
ist die Zusammenhangskomponente des Überlagerungsraumes der Garbe der
holomorphen Funktionen
,
welche ein fest gewähltes Urbild des Keimes
enthält.
Beispiel
und
sei der Keim desjenigen Zweiges der holomorphen Quadratwurzel mit
.
Die maximale analytische Fortsetzung
ist gegeben durch:
Zu einer anderen analytischen Fortsetzung
wird die Abbildung
definiert durch
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.10. 2020