Areasinus hyperbolicus und Areakosinus hyperbolicus

Areasinus hyperbolicus (abgekürzt $\operatorname {arsinh}$ oder $\operatorname {asinh}$ ) und Areakosinus hyperbolicus (abgekürzt $\operatorname {arcosh}$ oder $\operatorname {acosh}$ ) gehören zu den Areafunktionen und sind die Umkehrfunktionen von Sinus hyperbolicus und Kosinus hyperbolicus.

Definitionen

Die Funktionen lassen sich durch die folgenden Formeln ausdrücken:

Areasinus hyperbolicus:

$\operatorname {arsinh} (x)=\ln \left(x+{\sqrt {x^{2}+1}}\right)$ mit $\,x\in \mathbb {R}$

Areakosinus hyperbolicus:

$\operatorname {arcosh} (x)=\ln \left(x+{\sqrt {x^{2}-1}}\right)$ für $x \geq 1$

Hier steht $\ln$ für den natürlichen Logarithmus.

Umrechnung

Zusammen mit der Signumfunktion $\sgn$ gilt der Zusammenhang:

$\operatorname {arsinh} (x)=\operatorname {sgn} (x)\cdot \operatorname {arcosh} \left({\sqrt {x^{2}+1}}\right)$

Für $x \geq 1$ gilt:

$\operatorname {arcosh} (x)=\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)$

Eigenschaften

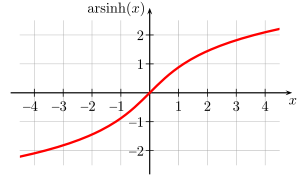
Graph der Funktion arsinh(x)

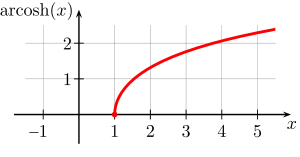
Graph der Funktion arcosh(x)

	Areasinus hyperbolicus	Areakosinus hyperbolicus
Definitionsbereich	$-\infty <x<+\infty$	$1\leq x<+\infty$
Wertebereich	$-\infty <f(x)<+\infty$	$0\leq f(x)<+\infty$
Periodizität	keine	keine
Monotonie	streng monoton steigend	streng monoton steigend
Symmetrien	Punktsymmetrie zum Ursprung, ungerade Funktion	keine
Asymptote	$f(x)\to \pm \ln(2\|x\|)$ für $x \to \pm \infty$	$f(x)\to \ln(2x)$ für $x \to +\infty$
Nullstellen
Sprungstellen	keine	keine
Polstellen	keine	keine
Extrema	keine	keine
Wendepunkte		keine

Reihenentwicklungen

Wie bei allen trigonometrischen und hyperbolischen Funktionen gibt es auch Reihenentwicklungen. Dabei treten die Doppelfakultät und die Verallgemeinerung des Binomialkoeffizienten auf.

Die Reihenentwicklungen lauten:

${\begin{alignedat}{2}\operatorname {arsinh} (x)&=x\sum _{k=0}^{\infty }{\frac {(2k-1)!!(-x^{2})^{k}}{(2k)!!(2k+1)}}=\sum _{k=0}^{\infty }{\frac {{\binom {-{\frac {1}{2}}}{k}}x^{2k+1}}{2k+1}}&{}\\&=x-{\frac {1}{2}}{\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}{\frac {x^{5}}{5}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}{\frac {x^{7}}{7}}+\cdots &{\text{ für }}|x|<1\\\operatorname {arsinh} (x)&=\operatorname {sgn} (x)\cdot \left[\ln(2|x|)-\sum _{k=1}^{\infty }{\frac {(2k-1)!!}{2k(2k)!!(-x^{2})^{k}}}\right]&{\text{ für }}|x|>1\\\operatorname {arcosh} (x)&=\ln(2x)-\sum _{k=1}^{\infty }{\frac {(2k-1)!!}{2k\cdot (2k)!!}}x^{-2k}&{}\end{alignedat}}$

Ableitungen

Die Ableitung des Areasinus hyperbolicus lautet:

${\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\operatorname {arsinh}(x)={\frac {1}{{\sqrt {x^{2}+1}}}}$

Die Ableitung des Areakosinus hyperbolicus lautet:

${\frac {{\mathrm {d}}}{{\mathrm {d}}x}}\operatorname {arcosh}(x)={\frac {1}{{\sqrt {x^{2}-1}}}}$ für x > 1

Stammfunktionen

Die Stammfunktionen des Areasinus hyperbolicus und des Areakosinus hyperbolicus lauten:

$\int \operatorname {arsinh} (x)\ \mathrm {d} x=x\cdot \operatorname {arsinh} (x)-{\sqrt {x^{2}+1}}+C$

$\int \operatorname {arcosh} (x)\ \mathrm {d} x=x\cdot \operatorname {arcosh} (x)-{\sqrt {x^{2}-1}}+C$

Andere Identitäten

${\begin{aligned}\operatorname {arcosh} (2x^{2}-1)=2\operatorname {arcosh} (x)\qquad {\text{ für }}x\geq 1\\\operatorname {arcosh} (8x^{4}-8x^{2}+1)=4\operatorname {arcosh} (x)\qquad {\text{ für }}x\geq 1\\\operatorname {arcosh} (2x^{2}+1)=2\operatorname {arsinh} (x)\qquad {\text{ für }}x\geq 0\\\operatorname {arcosh} (8x^{4}+8x^{2}+1)=4\operatorname {arsinh} (x)\qquad {\text{ für }}x\geq 0\end{aligned}}$

$\operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)$

$\operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)$

${\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}$

Numerische Berechnung

Grundsätzlich kann der Areasinus hyperbolicus über die bekannte Formel

$\operatorname {arsinh} (x)=\ln \left(x+{\sqrt {x^{2}+1}}\right)$

berechnet werden, wenn die natürliche Logarithmusfunktion $\ln x$ zur Verfügung steht. Es gibt jedoch folgende Probleme:

Große, positive Operanden lösen einen Überlauf aus, obwohl das Endergebnis immer darstellbar ist.
Für Operanden nahe an 0 kommt es zu einer numerischen Auslöschung, womit das Ergebnis ungenau wird.

Zunächst einmal soll der Operand positiv gemacht werden:

$\operatorname {arsinh} x=-\operatorname {arsinh} (-x)$ für x<0

angewandt.

Für $x\geq 0$ können dann folgende Fälle unterschieden werden:

Fall 1: ist eine große, positive Zahl mit $x\geq {10}^{\frac {k}{2}}$ :

$\operatorname {arsinh} x=\ln {2}+\ln {x},$

wobei die Anzahl der signifikanten Dezimalziffern des verwendeten Zahlentyps ist, was zum Beispiel beim 64-Bit-Gleitkommatyp double 16 ist.

Diese Formel ergibt sich aus folgender Überlegung:

${10}^{k}$ ist die kleinste positive Zahl, ab der die letzte Vorkommastelle nicht mehr gespeichert ist, weshalb ${10}^{k}+{1}\approx {10}^{k}$ gilt. Jetzt soll dasjenige berechnet werden, ab dem gilt: $x^{2}+1\approx {x}^{2}$ . Dies gilt für ${x}^{2}\geq {10}^{k}$ , woraus ${x}\geq {10}^{\frac {k}{2}}$ folgt. Somit kann man in der bekannten Formel für den Areasinus hyperbolicus x^2 + 1

durch $x^{2}$ ersetzen:

$\operatorname {arsinh} (x)=\ln \left(x+{\sqrt {x^{2}+1}}\right)$ ≈ $\ln(x+{\sqrt {x^{2}}})=\ln({2x})=\ln {2}+\ln {x}$

Fall 2: ist nahe an 0, z.B. für $x<0{,}125$ :

Verwendung der Taylorreihe:

$\operatorname {arsinh} x=x-{\frac {1}{2}}{\frac {x^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}{\frac {x^{5}}{5}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}{\frac {x^{7}}{7}}+\dotsb$