Evolute

Die Evolute (rot) einer Kurve (Parabel, blau) ist der geometrische Ort aller Krümmungsmittelpunkte oder auch die Einhüllende ihrer Normalen

Die Evolute einer ebenen Kurve ist

die Bahn, auf der sich der Mittelpunkt des Krümmungskreises bewegt, wenn der zugehörige Punkt die gegebene Kurve durchläuft.

Oder auch:

die Hüllkurve (Enveloppe) der Normalen der gegebenen Kurve.

Evoluten stehen in engem Zusammenhang mit den Evolventen einer gegebenen Kurve, denn es gilt: Eine Kurve ist die Evolute jeder ihrer Evolventen.

Evolute einer parametrisierten Kurve

Beschreibt ${\vec {x}}={\vec {c}}(t),\;t\in [t_{1},t_{2}]$ eine reguläre Kurve in der euklidischen Ebene, deren Krümmung nirgends 0 ist, und sind $\rho (t)$ der Krümmungskreisradius und ${\vec {n}}(t)$ die zum Krümmungsmittelpunkt weisende Einheitsnormale, so ist

${\vec {E}}(t)={\vec {c}}(t)+\rho (t){\vec {n}}(t)$

die Evolute der gegebenen Kurve.

Ist ${\vec {c}}(t)=(x(t),y(t))^{T}$ und ${\vec {E}}=(X,Y)^{T}$ , so ist

$\displaystyle X(t)=x(t)-{\frac {y'(t)\cdot {\Big (}x'(t)^{2}+y'(t)^{2}{\Big )}}{x'(t)\cdot y''(t)-x''(t)\cdot y'(t)}}$ und

$\displaystyle Y(t)=y(t)+{\frac {x'(t)\cdot {\Big (}x'(t)^{2}+y'(t)^{2}{\Big )}}{x'(t)\cdot y''(t)-x''(t)\cdot y'(t)}}$ .

Eigenschaften der Evolute

Evolute: Die Normale in P ist Tangente in M.

Um Eigenschaften einer regulären Kurve herzuleiten, ist es vorteilhaft, die Bogenlänge der gegebenen Kurve als Parameter zu verwenden. Denn dann gilt (s. Frenetsche Formeln) $\;|{\vec {c}}'|=1\;$ und $\;{\vec {n}}'=-{\vec {c}}'/\rho \;$ . Hieraus folgt für den Tangentenvektor der Evolute $\;{\vec {E}}={\vec {c}}+\rho {\vec {n}}\;$ :

${\vec {E}}'={\vec {c}}'+\rho '{\vec {n}}+\rho {\vec {n}}'=\rho '{\vec {n}}\;.$

Aus dieser Gleichung ergeben sich die folgenden Eigenschaften einer Evolute:

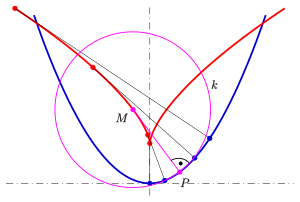
Die Evolute ist in Punkten mit $\rho '=0$ nicht regulär, d.h., sie hat in Punkten maximaler oder minimaler Krümmung Spitzen (s. Parabel, Ellipse, Nephroide).
Die Normalen der gegebenen Kurve sind Tangenten der Evolute, d.h.: Die Evolute ist die Einhüllende der Normalen der gegebenen Kurve.
In Abschnitten der gegebenen Kurve, in denen $\rho '>0$ bzw. $\rho '<0$ gilt, ist sie eine Evolvente ihrer Evolute. (Im Bild ist die blaue Parabel eine Evolvente der roten Neilschen Parabel.)

Beweis der letzten Eigenschaft:
In dem betrachteten Abschnitt sei $\rho '>0$ . Eine Evolvente der Evolute lässt sich folgendermaßen beschreiben:

${\vec {C}}_{0}={\vec {E}}-{\frac {{\vec {E}}'}{|{\vec {E}}'|}}\;{\Big (}\int _{0}^{s}|{\vec {E}}'(w)|\;\mathrm {d} w+l_{0}\;{\Big )}\;,$

wobei l_0 eine Fadenverlängerung bedeutet (s. Evolvente).
Mit ${\vec {E}}={\vec {c}}+\rho {\vec {n}}\;,\;{\vec {E}}'=\rho '{\vec {n}}$ und $\rho '>0$ ergibt sich

${\vec {C}}_{0}={\vec {c}}+\rho {\vec {n}}-{\vec {n}}\;{\Big (}\int _{0}^{s}\rho '(w)\;\mathrm {d} w\;+l_{0}{\Big )}={\vec {c}}+(\rho (0)-l_{0})\;{\vec {n}}\;.$

D. h., für die Fadenverlängerung $l_{0}=\rho (0)$ erhält man die gegebene Kurve wieder.

Parallele Kurven besitzen dieselbe Evolute.

Beweis: Eine zur gegebenen Kurve im Abstand parallele Kurve besitzt die Parameterdarstellung ${\vec {c}}_{d}={\vec {c}}+d{\vec {n}}$ und den Krümmungsradius (s. Parallelkurve) $\rho _{d}=\rho -d$ . Die Evolute der Parallelkurve ist also ${\vec {E}}_{d}={\vec {c}}_{d}+\rho _{d}{\vec {n}}={\vec {c}}+d{\vec {n}}+(\rho -d){\vec {n}}={\vec {c}}+\rho {\vec {n}}={\vec {E}}\;.$

Beispiele

Evolute der Normalparabel

Die Normalparabel lässt sich durch die Parameterdarstellung $(t,t^{2})$ beschreiben. Nach den obigen Formeln ergeben sich für die Evolute die folgenden Gleichungen:

$X=\cdots =-4t^{3}$

$Y=\cdots ={\frac {1}{2}}+3t^{2}$

Dies ist die Parameterdarstellung einer Neilschen Parabel.

Evolute (rot) einer Ellipse

Die Evolute der großen Nephroide (blau) ist die kleine Nephroide (rot)

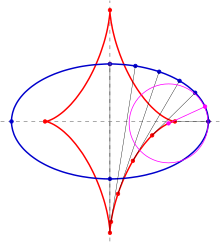
Evolute einer Ellipse

Für die Ellipse mit der Parameterdarstellung $(a\cos t,b\sin t)$ ergibt sich:

$X=\cdots ={\frac {a^{2}-b^{2}}{a}}\cos ^{3}t$

$Y=\cdots ={\frac {b^{2}-a^{2}}{b}}\sin ^{3}t$

Diese Gleichungen beschreiben eine schiefe Astroide. Elimination von liefert die implizite Darstellung

$(aX)^{\tfrac {2}{3}}+(bY)^{\tfrac {2}{3}}=(a^{2}-b^{2})^{\tfrac {2}{3}}\ .$

Evoluten bekannter Kurven

Zu einer Astroide: wiederum eine Astroide (doppelt so groß)
Zu einer Ellipse: eine schiefe Astroide
Zu einer Kardioide: wiederum eine Kardioide (ein Drittel so groß)
Zu einem Kreis: ein Punkt, nämlich dessen Mittelpunkt
Zu einer Deltoide: wiederum eine Deltoide (dreimal so groß)
Zu einer Zykloide: eine kongruente Zykloide
Zu einer Epizykloide: eine vergrößerte Epizykloide
Zu einer Hypozykloide: eine ähnliche Hypozykloide
Zu einer logarithmischen Spirale: die gleiche logarithmische Spirale
Zu einer Nephroide: wiederum eine Nephroide (halb so groß)
Zu einer Parabel: eine Neilsche Parabel
Zu einer Traktrix: eine Katenoide (Kettenlinie)

Literatur

K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und … Springer-Verlag, 2012, ISBN 3-8348-8346-8.
Kleine Enzyklopädie Mathematik. Harry Deutsch Verlag, 1977, ISBN 3-87144-323-9.

Basierend auf einem Artikel in:

Wikipedia.de