Elementarzelle

Die Bestandteile der Kristallstruktur: Gitter, Elementarzelle und Basis

Eine Elementarzelle oder Einheitszelle ist das von drei Basisvektoren ${\vec {a}}$ , ${\vec {b}}$ , ${\vec {c}}$ eines Kristallgitters gebildete Parallelepiped. Ihr Volumen ist das Spatprodukt ${\vec {a}}\cdot ({\vec {b}}\times {\vec {c}})$ der Basisvektoren. Den gesamten Kristall kann man sich aufgebaut denken aus der Verschiebung der Elementarzelle in alle drei Richtungen des Kristallgitters um ganzzahlige Vielfache der Basisvektoren. Die Überdeckung des Raumes durch die Elementarzellen ist lückenlos und überlappungsfrei. Die zweidimensionale Entsprechung in der Oberflächenkristallographie ist die Elementarmasche.

Beschreibung

Punktgitter mit einer kristallographischen Basis

Kubisch primitives Kristallgitter mit der Elementarzelle und den drei Basisvektoren in blau

Die Kristallstruktur ist eine dreidimensional periodische Wiederholung eines Motivs. Die Translationsvektoren, die einen Kristall mit sich zur Deckung bringen, heißen Gittervektoren. Sie bilden ein Punktgitter, eben das Kristallgitter G. Die Punkte dieses Gitters repräsentieren keine Atome, sie beschreiben lediglich die Periodizität der Struktur.

Drei beliebige Gittervektoren ${\vec {a}}$ , ${\vec {b}}$ , ${\vec {c}}$ , die nicht in einer Ebene liegen, bilden eine kristallographische Basis. Die Menge aller ganzzahligen Linearkombinationen dieser Basisvektoren bilden ein Gitter B, das im Allgemeinen eine Untermenge des Kristallgitters G ist.

$B:=\left\{\left.u{\vec {a}}+v{\vec {b}}+w{\vec {c}}\;\right|\,u,v,w\in \mathbb {Z} \right\}\subseteqq G$

Die drei Basisvektoren definieren auch ein Volumenelement V, die Fundamentalmasche des Gitters B:

$V:=\left\{\left.x{\vec {a}}+y{\vec {b}}+z{\vec {c}}\;\right|\,0\leq x,y,z<1\right\}$

Dieses Volumenelement ist die Elementarzelle des durch die Vektoren ${\vec {a}}$ , ${\vec {b}}$ , ${\vec {c}}$ beschriebenen Gitters. Es hat die Form eines Parallelepipeds. Enthält die Elementarzelle genau einen Gitterpunkt von G, dann heißt sie primitive Elementarzelle. In diesem Fall ist das Gitter B gleich dem Gitter G, andernfalls eine echte Untermenge.

Die Basisvektoren bilden das Koordinatensystem, mit dessen Hilfe der Kristall beschrieben wird. Man kann die Koordinaten sowohl als fraktionelle Koordinaten als auch in kartesischen Koordinaten ausdrücken.

Die Vektoren in G sind eindeutig bestimmt durch eine Symmetrieeigenschaft des Kristalls. Die Vektoren des Kristallgitters B dienen der Beschreibung des Kristalls. Daher kann man sie sich aus der Menge G geeignet auswählen. Für diese Auswahl gibt es allerdings Standards. (siehe unten)

Anwendung

Alle Punkte des Raumes lassen sich eindeutig einer Elementarzelle zuordnen. Diese ist um einen Kristallgittervektor vom Ursprung verschoben. Zwei Punkte des Raumes sind bezüglich des Kristallgitters äquivalent, wenn sie relativ zum Ursprung ihrer Elementarzelle dieselbe Position einnehmen. Somit teilt das Kristallgitter den Raum in Äquivalenzklassen ein. Jede Äquivalenzklasse besteht aus allen Punkten, die sich von einem gegebenen Punkt nur durch einen Translationsvektor des Kristallgitters unterscheiden.

Die Atome, die in einer Elementarzelle liegen, bilden die Basis des Kristalls. Zur Beschreibung des Kristalls ist es ausreichend, die Lage der Atome der Basis in der Elementarzelle anzugeben. Diese Atome können auch als Vertreter einer Äquivalenzklasse betrachtet werden. Bei der Diskussion von Kristallstrukturen wird der Begriff Atom der Basis oft auch stillschweigend in diesem Sinn verwendet.

Die primitive Elementarzelle

Kubisch primitive Elementarzelle.

Hat man die Basisvektoren so gewählt, dass das von ihnen gebildete Gitter B mit dem Kristallgitter G identisch ist, so nennt man diese Basis primitiv. Diese Vektoren beschreiben dann eine primitive Elementarzelle. Die Koordinaten der Punkte des Kristallgitters sind ganzzahlig.

Jede primitive Elementarzelle enthält nur einen Punkt des Kristallgitters. Sie ist die Elementarzelle mit dem kleinstmöglichen Volumen.

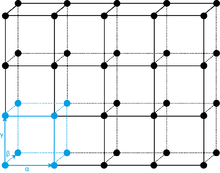
In dem Bild sind alle Punkte des Kristallgitters dargestellt. Nur ein Eckpunkt (0,0,0) gehört zur Elementarzelle.

Die zentrierte Elementarzelle

Kubisch innenzentrierte Elementarzelle.

Insbesondere dann, wenn man ein Achsensystem verwenden will, das den Symmetrieelementen der Raumgruppe des Kristalls angepasst ist, kommt man bei den meisten Kristallsystemen nicht umhin, auch nicht-primitive Elementarzellen zu verwenden. Das Kristallgitter enthält dann auch Punkte mit nicht ganzzahligen Koordinaten. Eine Elementarzelle enthält somit mehrere Punkte des Kristallgitters.

Diese Elementarzellen heißen zentriert. Ihr Volumen ist ein Vielfaches des Volumens der primitiven Elementarzelle. Zur Beschreibung aller möglichen Strukturen dreidimensionaler Kristalle mit einer konventionellen Zelle benötigt man 14 unterschiedliche Gitter. Dies sind die Bravais-Gitter.

In dem Bild sind alle Punkte des Kristallgitters dargestellt. Nur ein Eckpunkt (0,0,0) und der innere Punkt gehören zur Elementarzelle. In diesem Fall ist der Vektor (½, ½, ½) ein Vektor des Kristallgitters, der keine ganzzahligen Koordinaten hat.

Andere Zellen

Darstellung einer hexagonalen Elementarzelle (dunkle Linien).

Man kann eine lückenlose und überlappungsfreie Zerlegung des Raumes auch mit Zellen erreichen, die nicht die Form eines Parallelepipeds haben und somit keine Elementarzellen im eigentlichen Sinne sind.

Die bekannteste dieser Zellen ist die Wigner-Seitz-Zelle.

Zur Beschreibung von hexagonal dichtesten Kugelpackungen wird in der Literatur oft ein 6-eckiges Prisma als Zelle verwendet. Dieses Prisma ist keine Elementarzelle. Es dient in aller Regel auch nicht zur kristallographischen Beschreibung der Struktur, sondern nur zu deren Veranschaulichung.

Die asymmetrische Einheit

Bislang wurde als einzige Symmetrieoperation die Translation betrachtet. In einem Kristall können aber auch noch andere Symmetrieoperationen existieren: die Drehung, die Punktspiegelung, die Drehinversion, die Schraubung und die Gleitspiegelung. Die Menge aller Symmetrienoperationen eines Kristalls bilden seine Raumgruppe. Auch diese Symmetrieoperationen bilden den Kristall auf sich selbst ab. Insbesondere kann aber auch ein Teil der Elementarzelle durch eine solche Operation auf einen anderen Teil der Elementarzelle abgebildet werden. In diesem Falle sind die zwei Teile der Elementarzelle symmetrisch äquivalent zueinander. Ein Volumenelement des Kristalls, aus dem der Kristall unter Verwendung aller Symmetrieoperationen der Raumgruppe gebildet werden kann nennt man asymmetrische Einheit (engl. asymmetric unit). Sie ist in der Regel kleiner als die primitive Elementarzelle. Für jede Raumgruppe ist eine asymmetric unit in den International Tables angegeben.

Zur Problematik der unterschiedlichen Begriffe

Der Sprachgebrauch ist nicht immer eindeutig und auch international nicht einheitlich. Bei deutschsprachigen Kristallographen ist Elementarzelle der übliche Begriff, der gleichbedeutend mit englisch unit cell verwendet wird. Gleichbedeutend sind auch frz. maille élémentaire und ital. cella elementare. Diese Bezeichnungen werden meist im Sinne von „konventioneller Zelle“ (s. u.) verwendet, können aber auch eine primitive Zelle bezeichnen. Bemerkenswert ist, dass der französische Begriff bei älteren Autoren noch nicht vorkommt: Bravais verwendete parallélogramme générateur oder maille parallélogramme in zwei Dimensionen und parallélopipède générateur oder noyau („Kern“) in drei Dimensionen. Mallard schrieb einfach maille, Friedel maille simple. Eindeutig sind nur die Begriffe „primitive Zelle“ und „konventionelle Zelle“. Die Commission for Crystallographic Nomenclature of the International Union of Crystallography gibt dazu folgende Definitionen:

Primitive cell

Eine primitive Zelle (frz. maille primitive) ist eine Einheitszelle, die von den Basisvektoren einer primitiven Basis des direkten Gitters aufgespannt wird. Das heißt, dass jeder Gittervektor als ganzzahlige Linearkombination der drei Basisvektoren dargestellt werden kann

Unit cell

Die unit cell (dt. Einheitszelle, frz. maille) ist das von den drei Vektoren a, b, c einer kristallographischen Basis des direkten Gitters aufgespannte Parallelepiped. Ist die Basis primitiv, so heißt die Einheitszelle „primitive Zelle“ (primitive cell). Ist die Basis nicht primitiv, ist die Einheitszelle eine vielfache Zelle (multiple cell). Die Multiplizität ergibt sich aus dem Verhältnis ihres Volumens zum Volumen der primitiven Zelle.

Conventional cell

Die conventional cell (frz. maille conventionnelle) ist für jedes Gitter diejenige Zelle, die folgende Bedingungen erfüllt:

Ihre Basisvektoren definieren ein rechtshändiges Achsensystem.
Ihre Kanten verlaufen entlang von Symmetrieachsen des Gitters.
Es ist die kleinste Zelle, die die vorstehenden Bedingungen erfüllt.

Kristalle mit dem gleichen Typ von konventioneller Zelle gehören zur gleichen Kristallfamilie.

Literatur

Schwarzenbach D. Kristallographie Springer Verlag, Berlin 2001, ISBN 3-540-67114-5

Basierend auf einem Artikel in:

Wikipedia.de