Dipolantenne

Eine Dipolantenne (von lateinisch di ‚zwei‘; deutsch Zweipolantenne; auch Antennendipol) ist eine gestreckte Antenne, die aus einem (ggf. gefalteten) geraden Metallstab oder Draht besteht, der auch geteilt sein kann. Sie wandelt hochfrequenten Wechselstrom und elektromagnetische Wellen ineinander um, kann also sowohl zum Senden als auch zum Empfangen eingesetzt werden.
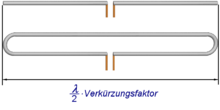
Die optimale Länge einer λ/2-Dipolantenne ist etwa die Hälfte der Wellenlänge λ des speisenden hochfrequenten Wechselstromes. Eine Verkürzung oder Verlängerung der Stäbe hat eine Änderung der Resonanzfrequenz zur Folge.
Geschichte
Das Prinzip der Dipolantenne geht auf den deutschen Physiker Heinrich Hertz zurück, der als Erster elektromagnetische Wellen experimentell nachweisen konnte. Sein Dipol (Hertzscher Dipol), der wesentlich kleiner als λ/8 war, hat nur noch theoretische Bedeutung. Die Verlängerung auf etwa λ/2 führt zu einer Resonanz, die die Anpassung der Antenne an die Speiseleitung erleichtert und den Wirkungsgrad erhöht. Der russische Physiker Alexander Stepanowitsch Popow verwendete 1895 erstmals eine Dipolantenne zum Empfang elektromagnetischer Wellen.
Grundlagen
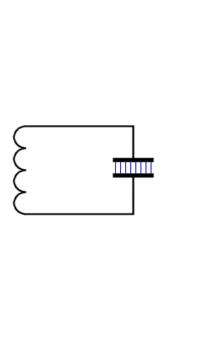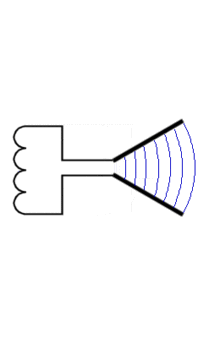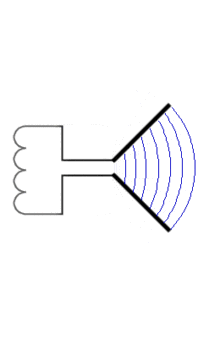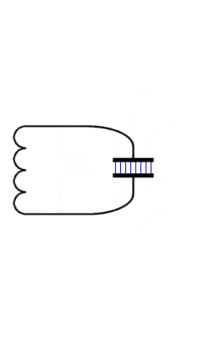
Die Animation rechts zeigt, wie man sich die Entstehung eines resonanten Dipols aus einem Schwingkreis vorstellen kann.
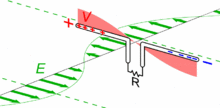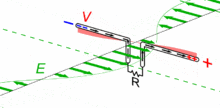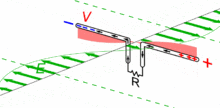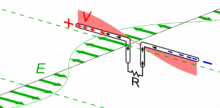
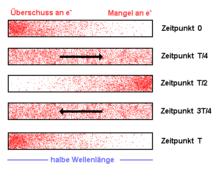
Das Bild rechts zeigt die Phasen einer Schwingung des λ/2-Dipols. Die elektrische Anregung möge zum Zeitpunkt null starten, wenn am linken Ende der größte Elektronenüberschuss herrscht. Gleichzeitig ist am rechten Ende das Potential besonders positiv, dort herrscht Elektronenmangel. Es fließt noch kein Strom.
Entgegengesetzte Ladungen ziehen sich an, deshalb bewegen sich viele Elektronen nach rechts. Eine Viertel-Periode später, zum Zeitpunkt T/4, misst man in der Mitte des Dipols ein Strommaximum, dort entsteht dann auch das stärkste Magnetfeld. Die Spannung längs des Dipols ist zu diesen Zeitpunkten ausgeglichen.
Das Magnetfeld verhindert, dass der Strom abrupt aufhört. Es treibt die Elektronen weiter auf die andere Seite. Genau eine halbe Schwingungsdauer nach dem Start (T/2) haben sich die Elektronendichten vertauscht und die höchste negative Spannung misst man nun am rechten Ende des Dipols. Der Strom ist zum Erliegen gekommen. Nun startet der entgegengesetzte Ausgleichsvorgang. Nach einer ganzen Periodendauer T ist der Anfangszustand wiederhergestellt.
Es gibt zwei Bauformen des Dipols:
- Er kann in der Mitte geteilt werden, um dort ein symmetrisches Kabel anzuschließen. Dessen Impedanz muss für Leistungsanpassung relativ gering (etwa 70 Ω) sein. Falls ein unsymmetrisches Koaxialkabel verwendet werden soll, ist an dieser Stelle ein Symmetrierglied (Balun) erforderlich.
- An einem Ende des Dipols kann ein unsymmetrisches Kabel angeschlossen werden, dessen Impedanz relativ hoch (möglichst 2200 Ω) ist. Falls ein niederohmiges Koaxialkabel verwendet werden soll, ist an dieser Stelle ein Resonanztransformator zur Leistungsanpassung erforderlich.
Impedanz
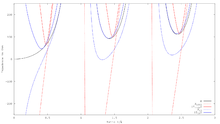
Die Dämpfung der Resonanz durch die Abstrahlung in den Freiraum bewirkt eine Verschiebung der Resonanz zu einer etwas kleineren Frequenz und einen komplexen Anteil an der Fußpunktimpedanz. Bei einem mittig gespeisten offenen Dipol der Länge λ/2 beträgt diese (73,1 + j 42,5) Ω.
Um die Frequenzverschiebung zu kompensieren und den Imaginärteil zu beseitigen, wird der λ/2-Dipol um den Faktor 0,96 verkürzt. Das gilt für einen Dipol, der unendlich dünn ist. Da aber in der Realität der Durchmesser der Dipolelemente > 0 ist, sinkt der Verkürzungsfaktor in Abhängigkeit vom Durchmesser weiter ab. Auch Gegenstände in der Nähe der Antenne erhöhen den Verkürzungsfaktor. Die primäre Ursache für die zusätzliche Verkürzung ist die Kapazität des Leiters gegen seine Umgebung. Mit dem Durchmesser steigt auch die Bandbreite einer Dipolantenne, was insbesondere bei Fächer- und Breitbanddipolen ausgenutzt wird. Für das λ/2-Dipol ergibt sich der Verkürzungsfaktor V aus der Dipollänge l und dem Durchmesser d zu:
Auch der Faltdipol ist eine Art des λ/2-Dipols. Bei ihm erfolgt die Speisung in der Mitte eines von zwei parallelen Leitern, die an den Enden miteinander verbunden sind. Seine Impedanz ist 4-mal höher als die des gestreckten λ/2-Dipols, da nur der halbe Strom über die Speisepunkte fließt. Das passt sehr gut zum Balun aus einer λ/2-Umwegleitung, der die Impedanz auf 1/4 reduziert und den Anschluss eines üblichen Koaxialkabels ermöglicht.
Richtdiagramm
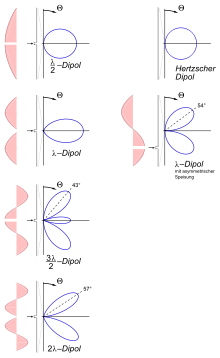
Das Richtdiagramm einer Antenne, das ist die Winkelabhängigkeit der Strahlungsintensität, lässt sich berechnen aus der Stromverteilung über die Länge des Leiters. Aus der näherungsweise sinusförmigen Stromverteilung auf dem λ/2-Dipol (links oben in der Abb. rechts) ergibt sich der Ausdruck
,
worin h bei vertikaler Antenne der Höhenwinkel ist. Zum Vergleich: Der entsprechende Ausdruck des Hertzschen Dipols lautet einfach cos(h), in der Abb. rechts daneben. Man sieht, dass die Abstrahlung des λ/2-Dipols etwas gerichteter ist: Die abgestrahlte Leistung ist bereits bei einem Höhenwinkel von 39° statt 45° auf die Hälfte abgesunken.
Die Integration der Winkelabhängigkeit über alle Richtungen liefert die Gesamtleistung und deren gleichmäßige Verteilung einen Bezugswert für die Strahlungsintensität (Isotropstrahler). Für den λ/2-Dipol ist die Strahlungsintensität in Hauptrichtung (h = 0) um einen Faktor G = 1,64 (2,15 dBi) höher als der Bezugswert. Beim Hertzschen Dipol beträgt dieser Antennengewinn G nur 1,5 (1,76 dBi). Bei einer Länge von 5/4 λ besitzt das Dipol seinen größten Gewinn von 5,2 dBi. Darüber bilden sich Nebenkeulen aus und erst bei einem viel größeren Dipol sind bessere Werte möglich. Daher finden sich 5/4-λ-Dipole als einfache Richtantennen, besonders in der Ausführung als Groundplane-Antenne mit 5/8-λ Länge. Allerdings ist eine Impedanzanpassung unbedingt erforderlich.
Eine leistungsangepasste Antenne entnimmt einer aus der Hauptrichtung einfallenden ebenen Welle eine Leistung, die ihrer Wirkfläche AW entspricht. Für den λ/2-Dipol beträgt diese:
Die Richtwirkung einer Dipolantenne kann durch Hinzufügung weiterer Elemente gesteigert werden, siehe dazu Yagi-Antenne.
In Fällen, bei denen die Richtwirkung gerade nicht erwünscht ist, z. B. bei angestrebtem Rundum-Empfang oder -Senden, kann man zu einem Knickdipol greifen, bei dem die beiden Metallstäbe im Winkel von 90° zueinander angeordnet sind.
Ganzwellendipole
Setzt man zwei ungespeiste Halbwellendipole längs aneinander und speist deren einander zugewandte Enden, entsteht ein Ganzwellendipol. An den Enden der λ/2-Elemente befinden sich Spannungsmaxima, Ganzwellendipole haben daher eine sehr hohe Speiseimpedanz (> 1 kΩ). Vorteilhaft gegenüber dem Halbwellendipol ist die leicht verbesserte Richtwirkung und damit ein erhöhter Antennengewinn.
Um Antennen aus zwei Halbwellendipolen zusammenzusetzen und übliche Kabelimpedanzen (etwa 50 Ω) zu erzielen, gibt es verschiedene Möglichkeiten:
- Man schaltet die Halbwellendipole zu einem Array zusammen und speist sie phasenrichtig parallel.
- Man ändert die Speiseimpedanz mit Hilfe eines Resonanztransformators.
- Man kann die Impedanz senken und zugleich die Bandbreite erhöhen, wenn man an Stelle dünner Stäbe Flächendipole wählt. Solche Ganzwellendipole aus zwei dreieckigen Flächen (oder gleichwertig x-förmig aus Stäben) werden auch als Strahler in Yagi-Antennen verwendet. Die passiven Elemente dieser Antennen dimensioniert man für den oberen Teil der Frequenzbandbreite des Flächendipols, so dass der Gewinn nach höheren Frequenzen hin ansteigt.
Ein weiteres Aneinanderfügen von Dipolen wird selten gemacht, weil sich dadurch im Strahlungsdiagramm unerwünschte „Nebenkeulen“ ergeben. Die Antenne „schielt“ dann.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.09. 2023