Leistungsanpassung

Werden eine elektrische Energiequelle und ein elektrischer Verbraucher in einer elektrischen Schaltung direkt miteinander verbunden, so wird unter Leistungsanpassung (auch Widerstandsanpassung und Lastanpassung) die Bedingung verstanden, unter der die maximal abgebbare oder verfügbare elektrische Leistung einer Quelle festgestellt wird. Ferner wird darunter eine Handlung verstanden, durch die die maximale Leistung an der Last erreicht wird.

Beispielsweise in der Mess-, Hochfrequenz- und Nachrichtentechnik bedeutet Anpassung die Herstellung eines Zusammenhangs zwischen der Ausgangsimpedanz einer Quelle und der Eingangsimpedanz des angeschlossenen Verbrauchers (Senke). Leistungsanpassung entsteht bei ohmschem Verhalten durch das Angleichen dieser Widerstände.

Diese Art der Anpassung ist bei Quellen erforderlich, die nur geringe elektrische Leistung liefern können, und deren Leistung möglichst umfassend weitergegeben werden soll. Solche schwachen Quellen sind beispielsweise Antennen und bestimmte Arten von Sensoren. Je vollständiger die Leistung ausgenutzt wird, desto besser kann ein Messsignal ohne Störüberlagerung oder eine Nachricht ohne Verluste an ihrem Inhalt übertragen und ausgewertet werden. Tatsächlich abgegeben wird bei linearen Quellen und Senken bestenfalls die Hälfte der verfügbaren Leistung; der Wirkungsgrad beträgt dann 50 %. Die andere Hälfte geht als Verlustleistung im Innenwiderstand der Quelle verloren.

Abgrenzung

Leistungsanpassung ist ein Begriff aus dem Bereich der linearen Netzwerke. Im Folgenden wird angenommen, dass der Innenwiderstand $R_{{\text{i}}}$ der Quelle und ihr Außenwiderstand $R_{\text{a}}$ , der Eingangswiderstand der Senke, lineare Widerstände sind.
Gängige elektrische Energiequellen zum Zwecke der Energieversorgung sollen mit möglichst hohem Wirkungsgrad nur die vom Verbraucher benötigte Leistung liefern; die Leistung im Verbraucher soll also gerade nicht maximiert werden. Ihre Auslegung erfolgt nicht auf Leistungsanpassung, sondern auf Spannungsanpassung (bei Spannungsquellen) oder Stromanpassung (bei Stromquellen); ihre Nennleistung würde also bereits weit vor einer (theoretischen) Leistungsanpassung überschritten.
Die Leistungsanpassung darf nicht mit der Leitungsanpassung verwechselt werden; bei letzterer geht es darum, bei der Übertragung von Signalen über eine elektrische Leitung störende Reflexionen von Wellen oder Impulsen zu vermeiden.

Belastung

Ohmsche Widerstände

Die von einer linearen Spannungsquelle übertragene Leistung wird bei sehr kleinen und bei sehr großen Außenwiderständen viel kleiner als die maximal abgebbare Leistung:

Wenn $R_{\text{i}}\gg R_{\text{a}}$ , dann bricht die Klemmenspannung nahezu zusammen, die Leistung am Außenwiderstand wird gering, die erzeugte Leistung wird fast vollständig am Innenwiderstand in Wärme umgewandelt.
Wenn $R_{\text{a}}\gg R_{\text{i}}$ , dann kommt fast kein Strom mehr zustande, was ebenfalls zu einer geringen Leistung am Außenwiderstand führt.

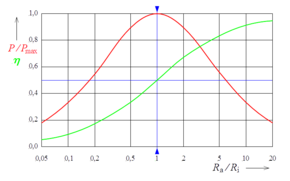
In rot die Darstellung der abgegebenen Leistung, bezogen auf die maximal abgebbare Leistung.
In grün der Verlauf des Wirkungsgrades einer linearen Spannungsquelle.
Beide Werte sind als Funktion der Relation $R_{\text{a}}$ zu $R_{{\text{i}}}$ aufgetragen.

Dazwischen liegt ein Maximum der Leistungsabgabe vor bei der sogenannten Widerstandsanpassung. Grafisch in nebenstehenden Diagramm ist dieser Betriebspunkt im rot dargestellten Kurvenverlauf bei maximaler relativer Leistung bei einem Widerstandsverhältnis von

${\frac {R_{\text{a}}}{R_{\text{i}}}}=1$

erreicht. Dieses erfordert

$R_{\text{i}}=R_{\text{a }}$ .

In diesem Fall ist die Ausgangsspannung die Hälfte der Leerlaufspannung $U_{0}$ , und die am Verbraucher nutzbare Leistung beträgt

$P_{\mathrm {max} }={\frac {{U_{0}}^{2}}{4\cdot R_{\text{i}}}}$ .

Der Wirkungsgrad $\eta$ , als grüne Linie im Diagramm dargestellt, ergibt sich zu

$\eta ={\frac {R_{\text{a}}}{R_{\text{a}}+R_{\text{i}}}}$

und beträgt bei Leistungsanpassung 50 %. In diesem Fall nimmt der Außenwiderstand dieselbe Leistung auf wie der Innenwiderstand der Quelle.

Impedanzen

Bei Wechselspannung und der dabei vorhandenen inneren Impedanz der Quelle ${\underline {Z}}_{\text{i}}=R_{\text{i}}+\mathrm {j} X_{\text{i}}$ und der äußeren Impedanz der Senke ${\underline {Z}}_{\text{a}}=R_{\text{a}}+\mathrm {j} X_{\text{a}}$ liegt eine Impedanzanpassung vor, wenn die konjugiert komplexen Werte der Impedanzen gleich sind

${\underline {Z}}_{\text{i}}={\underline {Z}}_{\text{a}}^{*}\qquad {\text{also}}\qquad R_{\text{i}}=R_{\text{a}}\qquad {\text{und}}\qquad X_{\text{i}}=-X_{\text{a }}$ .

Diese Anpassung existiert nur bei einer bestimmten Frequenz, bei der sich die Blindwiderstände herausheben. Die Quelle liefert dann ein Maximum an Wirkleistung an die Senke. Dieses beträgt in formaler Übereinstimmung mit dem Gleichstromkreis

$P_{\text{W, max}}={\frac {{U_{0}}^{2}}{4\cdot R_{\text{i}}}}$ .

In der Informationstechnik (nur dort) spielt die Impedanzanpassung auch als Scheinleistungsanpassung eine Rolle, die zugleich Reflexions- und Leitungsanpassung ist. Dazu wird die maximale Scheinleistung abgegeben:

${\underline {Z}}_{\text{i}}={\underline {Z}}_{\text{a }}$ .

Anwendung

Befinden sich mehrere Bauteile im Weg eines Hochfrequenzsignals, so muss jede Senke an ihre Quelle angepasst sein. Dabei zählen Leitungen in der Kette an ihrem Anfang als Senke und an ihrem Ende als Quelle. Baugruppen, die zusammengesetzt werden sollen, werden möglichst mit gleicher Impedanz hergestellt. In der Hochfrequenztechnik sind es üblicherweise 50 Ω. Sonst müssen Quelle und Senke durch ein Anpassnetzwerk aneinander angepasst werden. Bei rein ohmschen Impedanzen kann das Anpassnetzwerk ein Transformator sein, der die Impedanz der Quelle an die Senke anpasst.

Überall, wo Reflexionen auf Leitungen unbedingt vermieden werden müssen, wo also Leitungsanpassung erforderlich ist, kommt zugleich Leistungsanpassung zum Einsatz. Bei großen Hochfrequenzleistungen, wie sie bei Endstufen bei größeren Sendeanlagen auftreten, ist ein Wirkungsgrad von nur 50 % unerwünscht, weshalb eine kleinere Quellimpedanz gewählt wird, um einen höheren Wirkungsgrad zu erzielen. Leitungsanpassung liegt hier nur zwischen Leitung und Senke (Sendeantenne) vor, was zur Vermeidung von Signalreflexionen ausreichend ist. Durch verbesserte Technik herrscht immer öfter Spannungsanpassung statt Leistungsanpassung.

In Audioverstärkern ist der Ausgangswiderstand der Audioendstufe üblicherweise << 1 Ohm und damit deutlich weniger als ein Zehntel des Lastwiderstandes. Endstufen mit einem besonders geringen Ausgangswiderstand ermöglichen einen hohen Dämpfungsfaktor des Lautsprechers, wodurch dessen Eigenresonanzen gedämpft werden, indem die Rückinduktion einer (z.B. nach einem impulsiven/perkussiven Audiosignal) ausschwingenden Lautsprechermembran kurzgeschlossen wird. Angaben wie etwa „8 Ω“ beschreiben den minimalen Belastungswiderstand, den der Audioverstärker-Ausgang zu treiben vermag.

Eine Solarzelle gibt genau dann die maximale Leistung ab, wenn sie eben gerade beginnt, ihren Nennstrom zu liefern. Der Maximum Power Point (MPP) bedeutet hier per Definition Leistungsanpassung. Die Solarzelle ist jedoch keine lineare Quelle, ihre Kennlinie fällt in der Nähe der Schleusenspannung steil ab, daher ist der Punkt nicht bei $R_{\mathrm {senke} }=R_{\mathrm {quelle} }$ zu finden. (Ideale Stromquellen haben eine sehr hohe Quellimpedanz und sind zur Leistungsanpassung nicht geeignet.)

Literatur

Dieter Zastrow: Elektrotechnik, ein Grundlagenlehrbuch. 17. Auflage. Vieweg + Teubner, 2010, ISBN 978-3-8348-0562-1.

Basierend auf einem Artikel in:

Wikipedia.de