Zernike-Polynom

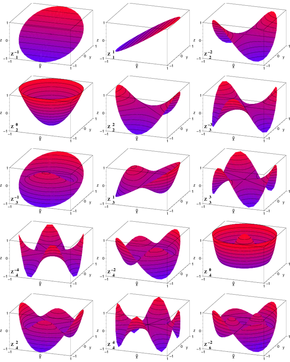
Zernike-Polynome bis zur 4. Ordnung und ein Beispiel 6. Ordnung

Die Zernike-Polynome sind nach Frits Zernike benannte orthogonale Polynome und spielen insbesondere in der Wellenoptik eine wichtige Rolle. Es gibt gerade und ungerade Zernike-Polynome. Die geraden Zernike-Polynome sind definiert durch:

$Z_{n}^{m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\cos(m\,\phi )$

und die ungeraden durch

$Z_{n}^{-m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\sin(m\,\phi ),$

wobei und nichtnegative ganze Zahlen sind, für die gilt: $n\geq m$ . $\phi$ ist der azimutale Winkel und $\rho$ ist der normierte radiale Abstand.

Die Radialpolynome $R_{n}^{m}$ sind definiert gemäß

$R_{n}^{m}(\rho )=\!\sum _{k=0}^{(n-m)/2}\!\!\!{\frac {(-1)^{k}\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!}}\;\rho ^{n-2\,k}$ ,

wenn n-m gerade ist und $R_{n}^{m}(\rho )=0$ , wenn n-m ungerade ist.

Häufig werden sie zu $R_{n}^{m}(1)=1$ normiert.

Eigenschaften

Zernike-Polynome sind ein Produkt eines radiusabhängigen Teils $R_{n}^{m}$ und eines winkelabhängigen Teils $G^{m}$ :

$Z_{n}^{\pm m}(\rho ,\phi )=R_{n}^{m}(\rho )\cdot G^{m}(\phi )\!.$

[Für Puristen sei darauf hingewiesen, dass in der Physik und Optik diese Funktionen zweier Argumente als Polynome bezeichnet werden, aber je nach Anwendung auch nur der Radialanteil, also die sinus-cosinus-förmigen Azimuth-Funktionen als zu trivial angesehen werden, um eine Namenserweiterung wie zum Beispiel auf Zernike-Funktionen zu bewirken.]

Eine Rotation des Koordinatensystems um den Winkel $\alpha =2\pi /m$ ändert den Wert des Polynoms nicht:

$G^{m}(\phi +\alpha )=G^{m}(\phi )\!.$

Der radiusabhängige Teil ist ein Polynom über $\rho$ vom Grad , welches keine Potenz kleiner enthält. $R_{n}^{m}$ ist eine gerade (ungerade) Funktion, wenn gerade (ungerade) ist.

Der radiusabhängige Teil stellt einen Spezialfall der Jacobi-Polynome $P_{n}^{(\alpha ,\beta )}(z)$ dar.

$R_{n}^{m}(\rho )=(-1)^{(n-m)/2}\rho ^{m}P_{(n-m)/2}^{(m,0)}(1-2\rho ^{2})$

Die Reihe der radiusabhängigen Polynome beginnt mit

$R_{0}^{0}(\rho )=1$

$R_{1}^{1}(\rho )=\rho$

$R_{2}^{0}(\rho )=2\rho ^{2}-1$

$R_{2}^{2}(\rho )=\rho ^{2}$

$R_{3}^{1}(\rho )=3\rho ^{3}-2\rho$

$R_{3}^{3}(\rho )=\rho ^{3}$

$R_{4}^{0}(\rho )=6\rho ^{4}-6\rho ^{2}+1$

$R_{4}^{2}(\rho )=4\rho ^{4}-3\rho ^{2}$

$R_{4}^{4}(\rho )=\rho ^{4}$

$R_{5}^{1}(\rho )=10\rho ^{5}-12\rho ^{3}+3\rho$

$R_{5}^{3}(\rho )=5\rho ^{5}-4\rho ^{3}$

$R_{5}^{5}(\rho )=\rho ^{5}$

$R_{6}^{0}(\rho )=20\rho ^{6}-30\rho ^{4}+12\rho ^{2}-1$

Allgemein ist $R_{n}^{n}(\rho )=\rho ^{n}.$

Anwendungen

In der Optik werden Zernike-Polynome benutzt um Wellenfronten zu repräsentieren, die wiederum die Abbildungsfehler optischer Systeme beschreiben. Dies findet zum Beispiel in der adaptiven Optik Anwendung.

Seit einigen Jahren ist die Verwendung der Zernike-Polynome auch in der Optometrie und Augenheilkunde üblich. Hier führen Abweichungen der Cornea beziehungsweise der Linse von der idealen Form zu Abbildungsfehlern.

Literatur

Frits Zernike: „Beugungstheorie des Schneidenverfahrens und seiner verbesserten Form, der Phasenkontrastmethode.“ Physica 1, 689–704, 1934.
Born and Wolf: Principles of Optics. Oxford: Pergamon, 1970.

Basierend auf einem Artikel in:

Wikipedia.de