Konvexitätsbedingung

In der mathematischen Theorie der normierten Räume werden gewisse Klassen normierter Räume durch Eigenschaften der Einheitskugel definiert. Hier betrachten wir Konvexitätsbedingungen, die die Konvexität der Einheitskugel verschärfen. Deren Ursprünge liegen in den 1930er Jahren, hier sind vor allem James A. Clarkson sowie Mark G. Krein und Naum I. Achijeser für grundlegende Begriffsbildungen zu nennen.

Daneben gibt es eine Reihe von Glattheitsbedingungen, die Differenzierbarkeitseigenschaften der Norm untersuchen. Über die Dualräume besteht eine enge Beziehung zwischen Konvexitätsbedingungen und Glattheitsbedingungen.

Konvexitätsbedingungen

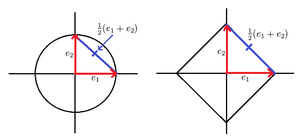
Es ist $\|\textstyle {\frac {1}{2}}(e_{1}+e_{2})\|$ im Fall der Summennorm (rechts) gleich 1, im Falle der euklidischen Norm (links) ist die Konvexitätsungleichung strikt.

Es sei $(X,\|\cdot \|)$ ein normierter Raum. In Formeln bedeutet die Konvexität der Einheitskugel

Für je zwei Vektoren $x,y\in X$ mit $\|x\|\leq 1,\,\|y\|\leq 1$ und $t\in [0,1]$ gilt $\|tx+(1-t)y\|\leq 1$ .

Dies schließt nicht aus, dass in vielen Fällen Gleichheit auch für verschiedene Vektoren und für 0<t<1 besteht, wie es zum Beispiel bei einem Quadrat als Einheitskugel vorliegt. Indem man das ausschließt oder noch stärkere Bedingungen stellt, kommt man zu den im Folgenden vorgestellten Raumklassen. Zur einfacheren Formulierung sei $(X,\|\cdot \|)$ stets ein normierter Raum mit

Einheitskugel $B_{X}:=\{x\in X;\,\|x\|\leq 1\}$

und Einheitssphäre $S_{X}:=\{x\in X;\,\|x\|=1\}$ .

Um Triviales auszuschließen, sei nicht der Nullraum X^* sei der Dualraum mit der durch $\|f\|:=\sup\{|f(x)|;\,x\in B_{X}\}$ definierten Dualraumnorm.

Strikt konvexe Räume

→ Hauptartikel: Strikt konvexer Raum

Will man die Gleichheit in der Konvexitätsformel weitestgehend ausschließen, also sicherstellen, dass die Einheitssphäre keine Strecken enthält, so führt dies zwanglos zu folgender Definition:

$(X,\|\cdot \|)$ heißt strikt konvex, falls gilt:

Sind $x,y\in S_{X}$ verschieden und ist 0<t<1

, so ist $\|tx+(1-t)y\|<1$ .

Gleichmäßig konvexe Räume

→ Hauptartikel: Gleichmäßig konvexer Raum

Indem man kontrolliert, wie gut die Ungleichung in der Definition des strikt konvexen Raums erfüllt ist, kommt man zu folgendem Begriff:

$(X,\|\cdot \|)$ heißt gleichmäßig konvex, falls gilt:

Für jedes $0<\varepsilon \leq 2$ ist $\inf\{1-{\frac {1}{2}}\|x+y\|;\,x,y\in S_{X},\|x-y\|\geq \varepsilon \}>0$ .

Lokal gleichmäßig konvexe Räume

Die Bedingung in der Definition der gleichmäßigen Konvexität gilt gleichmäßig für alle x,y . Indem man einen Vektor fest hält und das Infimum nur noch über den anderen bildet, erhält man folgende lokale Version:

$(X,\|\cdot \|)$ heißt lokal gleichmäßig konvex, falls gilt:

Für jedes $0<\varepsilon \leq 2$ und jedes $x\in S_{X}$ ist $\inf\{1-{\frac {1}{2}}\|x+y\|;\,y\in S_{X},\|x-y\|\geq \varepsilon \}>0$ .

Schwach gleichmäßig konvexe Räume

In der Definition der gleichmäßigen Konvexität kann die Bedingung $\|x-y\|\geq \varepsilon$ in der Menge, über die das infimum gebildet wird, zu $|f(x-y)|\geq \varepsilon$ abgeschwächt werden, wobei $f\in S_{{X^{*}}}$ ist, also aus der Einheitssphäre des Dualraums stammt.

$(X,\|\cdot \|)$ heißt schwach gleichmäßig konvex, falls gilt

Für jedes $0<\varepsilon \leq 2$ und $f\in S_{{X^{*}}}$ ist $\inf\{1-{\frac {1}{2}}\|x+y\|;\,x,y\in S_{X},|f(x-y)|\geq \varepsilon \}>0$ .

Lokal schwach gleichmäßig konvexe Räume

Die Bedingung in der Definition der schwach gleichmäßigen Konvexität lässt sich wieder zu einer lokalen Version abschwächen:

$(X,\|\cdot \|)$ heißt lokal schwach gleichmäßig konvex, falls gilt:

Für jedes $0<\varepsilon \leq 2$ , $x\in S_{X}$ und $f\in S_{{X^{*}}}$ ist $\inf\{1-{\frac {1}{2}}\|x+y\|;\,y\in S_{X},|f(x-y)|\geq \varepsilon \}>0$ .

Lokal gleichmäßig mittelpunktskonvexe Räume

Aus der gleichmäßigen Konvexität folgt, dass für zwei Folgen $(x_{n})_{n}$ und $(y_{n})_{n}$ in $S_{X}$ , für die die Norm der Folge der Mittelpunkte $\textstyle {\frac {1}{2}}(x_{n}+y_{n})$ gegen 1 konvergiert, $\|x_{n}-y_{n}\|\rightarrow 0$ gelten muss. Diese Bedingung lässt sich durch die Forderung, dass die Folge der Mittelpunkte tatsächlich gegen ein Element der Einheitssphäre konvergieren muss, abschwächen:

$(X,\|\cdot \|)$ heißt lokal gleichmäßig mittelpunktskonvex, falls gilt:

Sind $(x_{n})_{n}$ und $(y_{n})_{n}$ Folgen in $S_{X}$ und konvergiert $\textstyle {\frac {1}{2}}(x_{n}+y_{n})\rightarrow z\in S_{X}$ , so gilt $\|x_{n}-y_{n}\|\rightarrow 0$ .

In jeder Richtung gleichmäßig konvexe Räume

→ Hauptartikel: UCED-Raum

Eine weitere Verallgemeinerung ergibt sich, wenn man nur dann auf $\|x_{n}-y_{n}\|\rightarrow 0$ schließen kann, wenn die Differenzen $x_{n}-y_{n}$ alle dieselbe Richtung haben.

$(X,\|\cdot \|)$ heißt gleichmäßig konvex in Richtung $z\in X\setminus \{0\}$ , falls gilt:

Sind $(x_{n})_{n}$ und $(y_{n})_{n}$ Folgen in $S_{X}$ und konvergiert $\textstyle {\frac {1}{2}}(x_{n}+y_{n})\rightarrow z\in S_{X}$ und ist $x_{n}-y_{n}\in \mathbb{R} z$ für alle , so gilt $\|x_{n}-y_{n}\|\rightarrow 0$ .

$(X,\|\cdot \|)$ heißt in jeder Richtung gleichmäßig konvex oder auch UCED-Raum, wenn $(X,\|\cdot \|)$ für alle $z\in X\setminus \{0\}$ gleichmäßig konvex in Richtung ist.

Stark konvexe Räume

Der nicht-leere Durchschnitt aus Kugel und konvexer Menge wird beliebig klein.

Um wie in der Verschärfung der Konvexität zur strikten Konvexität zu erreichen, dass die Einheitssphäre keine Strecken erhält, kann man Durchschnitte der Kugeln $rB_{X}$ mit Radius mit einer konvexen Menge betrachten und fordern, dass der Durchmesser ${\mathrm {diam}}(rB_{X}\cap C)$ der nicht-leeren Durchschnitte mit fallendem Radius gegen 0 geht.

$(X,\|\cdot \|)$ heißt stark konvex, falls gilt:

Für jede konvexe Menge $C\subset X$ gilt ${\mathrm {diam}}(rB_{X}\cap C)\rightarrow 0$ für $r\searrow \inf\{t>0;\,tB_{X}\cap C\not =\emptyset \}$ .

Schwach* gleichmäßig konvexe Räume

Obige Abschwächung der gleichmäßigen Konvexität unter Benutzung der schwachen Topologie kann auf dem Dualraum mit der schwach-*-Topologie formuliert werden:

Der Dualraum $(X^{*},\|\cdot \|)$ heißt schwach* gleichmäßig konvex, falls gilt:

Für jedes $0<\varepsilon \leq 2$ und $x\in S_{X}$ ist $\inf\{1-{\frac {1}{2}}\|f+g\|;\,f,g\in S_{{X^{*}}},|(f-g)x|\geq \varepsilon \}>0$ .

Übersicht

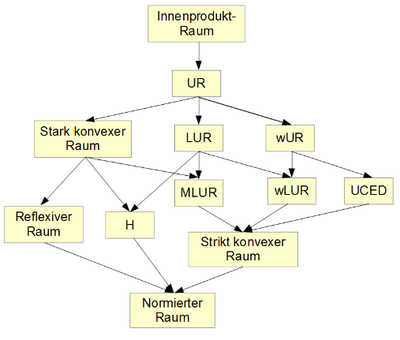
Zusammenhänge zwischen den Raumklassen

Dieses Diagramm gibt eine Übersicht über die Zusammenhänge zwischen den Raumklassen, wobei die Klasse der Innenprodukt-Räume die speziellste ist. Ein Pfeil von einer Klasse in die andere bedeutet, dass jeder normierte Raum der ersten Klasse auch der zweiten angehört. Die Reflexivität eines normierten Raums bedeutet, dass die Vervollständigung ein reflexiver Raum ist. Man beachte, dass mit Ausnahme der Reflexivität und natürlich der untersten Eigenschaft, ein normierter Raum zu sein, jede der Eigenschaften beim Übergang zu einer äquivalenten Norm verloren gehen kann. Folgende Standard-Abkürzungen, die zum Teil auf die entsprechenden englischen Bezeichnungen zurückgehen, wurden verwendet:

UR: gleichmäßig konvex (uniformly rotund)
LUR: lokal gleichmäßig konvex (locally uniformly rotund)
wUR: schwach gleichmäßig konvex (weakly uniformly rotund)
MLUR: lokal gleichmäßig mittelpunktskonvex (midpoint locally uniformly rotund)
UCED: in jede Richtung gleichmäßig konvex (uniformly convex in each direction)
wLUR: schwach lokal gleichmäßig konvex (weakly locally uniformly rotund)
H: Radon-Riesz-Eigenschaft (keine englische Abkürzung)

Dualräume

Viele der hier vorgestellten Konvexitätsbedingungen entsprechen Glattheitsbedingungen auf dem Dualraum. Die hier geltenden Beziehungen sind im Artikel zu den Glattheitsbedingungen zusammengestellt.

Konvexitätsmodul

Für einen normierten Raum $(X,\|\cdot \|)$ heißt die Abbildung

$\delta _{X}:[0,2]\rightarrow [0,1],\delta _{X}(t):=\inf\{1-{\frac {1}{2}}\|x+y\|;\,x,y\in E,\|x\|\leq 1,\|y\|\leq 1,\|x-y\|=t\}$

der Konvexitätsmodul. Dieser ist eine monoton wachsende Funktion, die in 0 den Wert 0 hat, sogar die Abbildung $t\mapsto \delta _{X}(t)/t$ ist monoton wachsend. Damit können zwei Räume bezüglich ihrer Konvexitätseigenschaften verglichen werden; man kann einen Raum $(X,\|\cdot \|)$ konvexer als einen Raum $(Y,\|\cdot \|)$ nennen, wenn $\delta _{X}(t)\geq \delta _{Y}(t)$ für alle $t\in [0,2]$ .

Ein normierter Raum ist genau dann gleichmäßig konvex, wenn $\delta _{X}(t)>0$ für alle t>0 .

Für den Folgenraum $c_{0}$ der Nullfolgen mit der Supremumsnorm gilt offenbar

$\delta _{{c_{0}}}(t)=0$ für alle $t\in [0,2]$ ,

denn für $e_{1}:=(1,0,0,\ldots ),e_{2}:=(0,1,0,0,\ldots )\in c_{0}$ und jedes $t\in [0,2]$ ist

$\textstyle \|(e_{1}\pm {\frac {t}{2}}e_{2})\|=\|(1,\pm {\frac {t}{2}},0,\ldots )\|=1,\,\,\|(e_{1}+{\frac {t}{2}}e_{2})-(e_{1}-{\frac {t}{2}}e_{2})\|=\|(0,t,0,0,\ldots )\|=t$ und daher

$\textstyle \delta _{{c_{0}}}(t)\leq 1-{\frac {1}{2}}\|(e_{1}+{\frac {t}{2}}e_{2})+(e_{1}-{\frac {t}{2}}e_{2})\|=1-{\frac {1}{2}}\|(2,0,0,\ldots )\|=0$ .

Für einen Hilbertraum folgt unter Verwendung der Parallelogrammgleichung

$\delta _{H}(t)=1-{\sqrt {1-\left({\frac {t}{2}}\right)^{2}}}$ für alle $t\in [0,2]$

und es gilt

$\delta _{X}(t)\leq \delta _{H}(t)$ für alle gleichmäßig konvexen Räume . In diesem Sinne sind die Hilberträume die "konvexesten" Räume.

Basierend auf einem Artikel in:

Wikipedia.de