Hausdorff-Metrik
Die Hausdorff-Metrik, benannt nach dem Mathematiker
Felix Hausdorff, misst
den Abstand
zwischen nichtleeren kompakten
Teilmengen
,
eines metrischen
Raums
.
Anschaulich haben zwei kompakte Teilmengen einen geringen Hausdorff-Abstand, wenn es zu jedem Element der einen Menge ein Element der anderen Menge gibt, zu dem dieses einen geringen Abstand hat.
Definition
Als Hilfsmittel definiert man den Abstand
zwischen einem Punkt
und einer nichtleeren kompakten Teilmenge
unter Rückgriff auf die Metrik
des Raums
als
Dann definiert man den Hausdorff-Abstand zwischen zwei nichtleeren
kompakten Teilmengen
und
als
Man kann zeigen, dass
in der Tat eine Metrik auf der Menge aller kompakten Teilmengen von
ist.
Äquivalent kann man den Hausdorff-Abstand definieren als
,
wobei
,
dies ist die Menge aller Punkte mit einem Abstand
zur Menge
.
Anwendungen
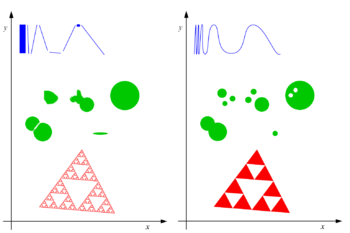
In der Theorie der iterierten Funktionensysteme werden Fraktale als Folgengrenzwerte im Sinne der Hausdorff-Metrik erzeugt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.05. 2021