Direkte Summe abelscher Gruppen

Der Begriff direkte Summe abelscher Gruppen verallgemeinert den Begriff der direkten Summe von Vektorräumen. Er ist von großer Bedeutung für die Theorie abelscher Gruppen. Kann eine Gruppe in eine direkte Summe zerlegt werden, so wird dadurch die Struktur der Gruppe auf einfachere Gruppen zurückgeführt. Neue Gruppen können aus den direkten Summanden gebildet werden. Die meisten Struktursätze machen eine Aussage über eine direkte Zerlegung von Gruppen.

Definitionen

Die abelsche Gruppe heißt genau dann direkte Summe zweier Untergruppen $A_{1}$ , $A_{2}$ , wenn folgende zwei Bedingungen erfüllt sind.

$A_{1}+A_{2}=A$ .
$A_{1}\cap A_{2}=0$ .

In diesem Fall wird geschrieben $A=A_{1}\oplus A_{2}$ . Dabei bezeichnet $0$ die Untergruppe, die nur das neutrale Element $0$ enthält.

Eine Untergruppe $A_{1}\hookrightarrow A$ heißt direkter Summand, wenn es eine Untergruppe $A_{2}$ gibt mit: $A=A_{1}\oplus A_{2}$ . In diesem Fall heißt $A_{2}$ Komplement von $A_{1}$ .
heißt direkt unzerlegbar, wenn und $0$ die einzigen direkten Summanden von sind.
Sei $(A_i|i \in I)$ eine Familie von Untergruppen von . Die Gruppe heißt direkte Summe der $(A_i|i \in I)$ , wenn folgende Bedingungen erfüllt sind.

$\sum _{i\in I}A_{i}=A$ . Die Familie $(A_i|i \in I)$ erzeugt .
Für jedes $i \in I$ gilt: $A_{i}\cap \sum _{j\neq i}A_{j}=0$ .

Es wird geschrieben: $A=\bigoplus \limits _{i\in I}A_{i}$ . Oder $A=A_{1}\oplus \dots \oplus A_{n}$ falls $I=\{1,\dots ,n\}$ .

Erläuterungen, einfache Sätze

Es seien Untergruppen der abelschen Gruppe . Dann sind folgende Aussagen äquivalent:
- Es ist $A=B\oplus C$ .
- Jedes $a\in A$ lässt sich eindeutig schreiben als $a=b+c$ mit $b\in B,c\in C$ .
- Es ist $A=B+C$ und aus $0=b+c$ mit $b\in B,c\in C$ folgt $b=0=c$ .
Ist $A=B\oplus C$ , so haben die beiden Endomorphismen $\pi _{B}\colon A\ni b+c\mapsto b\in A$ und $\pi _{C}\colon a\ni b+c\mapsto c\in A$ die folgende Eigenschaft: $\pi _{B}^{2}=\pi _{B},\pi _{C}^{2}=\pi _{C},\pi _{C}\pi _{B}=\pi _{B}\pi _{C}=0$ und $1_{A}=\pi _{B}+\pi _{C}$ . Dabei ist $1_{A}$ die Identität auf .

Homomorphismen liefern eine Möglichkeit, direkte Summanden zu kennzeichnen und zu erkennen:

Seien $A{\overset {f}{\longrightarrow }}B{\overset {g}{\longrightarrow }}C$ Homomorphismen. Dann gilt:

$gf$ ist ein Monomorphismus $\iff \operatorname {Bild} (f)\cap \operatorname {Kern} (g)=0$ und ist ein Monomorphismus.
Ist $gf$ ein Epimorphismus, dann ist $\operatorname {Bild} (f)+\operatorname {Kern} (g)=B$ .
Ist $gf$ ein Isomorphismus, dann ist $\operatorname {Bild} (f)\oplus \operatorname {Kern} (g)=B$ .

Für eine Untergruppe $B\hookrightarrow A$ sind folgende Aussagen äquivalent:

ist direkter Summand in .
Es gibt einen Endomorphismus $\pi \colon A\to A$ mit: $\pi ^{2}=\pi$ und $\pi (A)=B$ .
Ist $\iota \colon B\to A$ die Inklusionsabbildung, so gibt es einen Homomorphismus $\pi \colon A\to B$ mit $\pi \iota =1_{B}$ .

Beispiele

$0$ ist direkter Summand in jeder Gruppe.
Es sei die zyklische Gruppe $A=\mathbb {Z} /6\mathbb {Z} =\{0,1,2,3,4,5\}$ mit der zugehörigen Addition. Es sei $U=\{0,3\},V=\{0,2,4\}$ . Dann ist $A=U\oplus V$ . Es sind und Untergruppen von . Ihr Durchschnitt ist $0$ und ihre Summe ist . Es ist beispielsweise $3+4=1{\bmod {6}}$ .
Die Gruppen der ganzen Zahlen $\mathbb {Z}$ und der rationalen Zahlen $\mathbb{Q}$ sind unzerlegbar. Ist eine Primzahl, so ist $\mathbb {Z} /p\mathbb {Z}$ direkt unzerlegbar.
Hat die abelsche Gruppe eine größte Untergruppe $\neq A$ , dann ist direkt unzerlegbar. Ist eine Primzahl, so hat $A=\mathbb {Z} /p^{n}\mathbb {Z}$ die größte Untergruppe $p\mathbb {Z} /p^{n}\mathbb {Z} \neq A$ . Also ist direkt unzerlegbar.
Sind teilerfremde ganze Zahlen, so ist $\mathbb {Z} /(a\cdot b)\mathbb {Z} =a\mathbb {Z} /(a\cdot b)\mathbb {Z} \oplus b\mathbb {Z} /(a\cdot b)\mathbb {Z}$ .
Das letzte Beispiel hat eine starke Verallgemeinerung: Sei eine Gruppe und $n\in \mathbb {N}$ mit $A\cdot n=0$ . Außerdem sei $n=r\cdot s$ mit teilerfremden $r,s$ . Dann ist $A=A\cdot r\oplus A\cdot s$ .
Ist $\mathbb {Z} ^{2}=\{(z_{1},z_{2})|z_{1},z_{2}\in \mathbb {Z} \}$ , so ist $\mathbb {Z} ^{2}={\vec {e_{1}}}\mathbb {Z} \oplus {\vec {e_{2}}}\mathbb {Z}$ , wobei ${\vec {e_{1}}}=(1,0),{\vec {e_{2}}}=(0,1)$ ist. Das Komplement von ${\vec {e_{1}}}\mathbb {Z}$ ist keineswegs eindeutig bestimmt. Es ist zum Beispiel auch $\mathbb {Z} ^{2}={\vec {e_{1}}}\mathbb {Z} \oplus (z,1)\mathbb {Z}$ für alle $z\in \mathbb {Z}$ .
Das letzte Beispiel gilt allgemeiner. Sei $n\geq 1$ eine natürliche Zahl. $\mathbb {Z} ^{n}:=\{(z_{1},\dots ,z_{n})|z_{i}\in \mathbb {Z} \}$ die Menge der - Tupel mit Komponenten aus $\Z$ . Weiter sei ${\vec {e_{i}}}$ das Tupel, das an der Stelle eine hat und an anderen Stellen $0$ . Dann ist $\mathbb {Z} ^{n}=\bigoplus \limits _{i=1}^{n}{\vec {e}}_{i}\mathbb {Z}$ .
Um zu bestimmen, ob eine Untergruppe von $\mathbb {Z} ^{2}$ direkter Summand ist, gibt es ein einfaches Kriterium:

Sei ${\vec {a}}=(a_{1},a_{2})\in \mathbb {Z} ^{2}$ . Dann sind folgende Aussagen äquivalent.

${\vec {a}}\mathbb {Z}$ ist direkter Summand in $\mathbb {Z} ^{2}$ .
Es gibt $b_{1},b_{2}\in \mathbb {Z}$ mit $a_{1}\cdot b_{1}+a_{2}\cdot b_{2}=1$ .

Einige Gitter und Determinante als Flächeninhalt
Ein Gitter mit den erzeugenden Vektoren $(1,0)\mathbb {Z} ,(0,1)\mathbb {Z}$
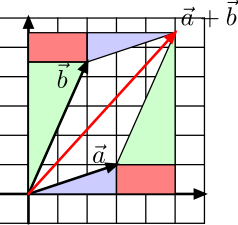Die Determinante als Flächeninhalt
Ein Gitter mit den erzeugenden Vektoren $(1,1)\mathbb {Z} ,(-2,-1)\mathbb {Z}$ wird dargestellt

Die Eigenschaft 2. des letzten Satzes hat eine geometrische Bedeutung: Die Untergruppe ${\vec {a}}\mathbb {Z}$ ist genau dann direkter Summand in $\mathbb {Z} ^{2}$ , wenn es einen Vektor ${\vec {b}}=(b_{1},b_{2})$ gibt, so dass ${\vec {a}},{\vec {b}}$ ein Parallelogramm vom Flächeninhalt 1 aufspannen.

Die letzte Aussage lässt sich verallgemeinern. Ist ${\vec {a}}=(a_{1},\dots ,a_{n})\in \mathbb {Z} ^{n}$ so gilt: ${\vec {a}}\mathbb {Z}$ ist genau dann direkter Summand in $\mathbb {Z} ^{n}$ , wenn die Zahlen $a_{1},\dots ,a_{n}$ den größten gemeinsamen Teiler haben.

Primäre Gruppen

Der folgende Satz macht eine Aussage über die Zerlegung von Torsionsgruppen. Dazu wird definiert: Sei eine Primzahl. Die Gruppe heißt -primär genau dann, wenn es zu jedem $a\in A$ ein $n\in \mathbb {N}$ gibt mit $a\cdot p^{n}=0$ . Die Summe aller -primären Untergruppen einer Gruppe ist -primär. Es ist die größte -primäre Untergruppe von . Sie wird mit $A_{p}$ bezeichnet und heißt -Primärkomponente von . Es gilt:

Ist eine Torsionsgruppe, so ist $A=\bigoplus \limits _{p{\text{ prim}}}A_{p}$ . Es ist direkte Summe seiner Primärkomponenten.

Universelle Eigenschaft

Sei $A=A_{1}+A_{2}$ für zwei Untergruppen $A_{1},A_{2}$ und $q_{i}\colon A_{i}\hookrightarrow A$ die kanonischen Inklusionen. Es sind äquivalent:

$A=A_{1}\oplus A_{2}$ .
Zu je zwei Homomorphismen $f_{i}\colon A_{i}\to B,i\in \{1,2\}$ gibt es genau einen Homomorphismus $f\colon A\to B$ mit $f\circ q_{i}=f_{i}$ für $i\in \{1,2\}$ .

Die zweite Aussage des Satzes ist die sogenannte universelle Eigenschaft der direkten Summe. Sie gilt für beliebige Indexmengen.

Sei $(A_{i}|i \in I)$ eine Familie von Untergruppen mit $\sum \limits _{i\in I}A_{i}=A$ . Und $q_{i}\colon A_{i}\hookrightarrow A$ seien die Inklusionen. Dann sind äquivalent:

Es ist $\bigoplus \limits _{i\in I}A_{i}=A$ .
Zu jeder Familie von Homomorphismen $f_{i}\colon A_{i}\to B$ gibt es genau ein $f\colon A\to B$ mit $f\circ q_{i}=f_{i}$ . Das heißt, folgendes Diagramm ist für alle $i\in I$ kommutativ.

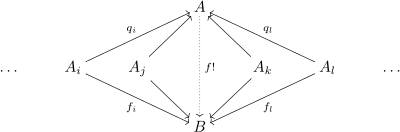
Seien $(A,q_{i})$ und $(S,s_{i})$ zwei abelsche Gruppen mit $q_{i}\colon A_{i}\to A$ und $s_{i}\colon A_{i}\to S$ . Gibt es zu jeder Familie $f_{i}\colon A_{i}\to B$ genau ein $f\colon A\to B$ mit $f_{i}=f\circ q_{i}$ und genau ein $g\colon S\to B$ mit $f_{i}=g\circ s_{i}$ , so sind und isomorph.

Einige Struktursätze

Satz: Ist $f\colon A\to \mathbb {Z}$ ein Homomorphismus, so ist $A=\operatorname {Kern} (f)\oplus a\mathbb {Z}$ mit $a\in A$ und $a\cdot \mathbb {Z} \cong \mathbb {Z}$ .
Satz: Jede Untergruppe von $\mathbb {Z} ^{n}$ ist direkte Summe von höchstens zyklischen Untergruppen.
Satz: Ist torsionsfrei und von Elementen erzeugt, so gibt es einen Monomorphismus $F\to \mathbb {Z} ^{n}$ .
Folgerung: Ist eine von Elementen erzeugte torsionsfreie Gruppe, so gibt es ein $k\leq n$ , so dass isomorph zu $\mathbb {Z} ^{k}$ ist.
Ist endlich erzeugt, so ist die Torsionsuntergruppe direkter Summand von .

Literatur

Friedrich Kasch: Moduln und Ringe. Teubner, Stuttgart 1977, ISBN 3-519-02211-7

Basierend auf einem Artikel in:

Wikipedia.de