j-Funktion

j-Funktion in der komplexen Ebene (ohne Faktor 12^3)

Die j-Funktion oder absolute Invariante (j-Invariante, Klein-Invariante) spielt eine wichtige Rolle in der Theorie der elliptischen Funktionen und Modulformen, denn man kann zeigen, dass zwei Gitter genau dann ähnlich sind, wenn ihre j-Invarianten übereinstimmen. Sie ist eine grundlegende Modulfunktion in dem Sinne, dass sich alle weiteren Modulfunktionen aus ihr durch rationale Funktionen ergeben.

Definition

Für $\tau \in \mathbb {H} :=\{z\in \mathbb {C} ;\Im (z)>0\}$ (obere Halbebene) ist

$j(\tau ):=12^{3}\cdot {\frac {g_{2}^{3}(\tau )}{\Delta (\tau )}}$ ,

dabei ist $\Delta (\tau ):=g_{2}^{3}(\tau )-27g_{3}^{2}(\tau )$ die Diskriminante; $g_{2}(\tau )=60G_{4}(\tau )$ und $g_{3}(\tau )=140G_{6}(\tau )$ sind die Eisensteinreihen zum Gitter ${\mathbb {Z}}\tau +{\mathbb {Z}}$ .

Eigenschaften

Fundamentalbereich (blau) der j-Funktion

Die j-Funktion ist holomorph auf $\mathbb {H}$ (sie hat nur einen einfachen Pol in der Spitze, also für $\Im (z)\to \infty$ )^[1], die Bezeichnung absolute Invariante erklärt sich aus dem Transformationsverhalten unter den Substitutionen der Modulgruppe $\Gamma :=SL_{2}(\mathbb {Z} )=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\mid a,b,c,d\in \mathbb {Z} ,ad-bc=1\right\}$ , es gilt nämlich:

$j\left({\frac {a\tau +b}{c\tau +d}}\right)=j(\tau )$ , d. h.

ist eine Modulfunktion.

Die j-Funktion bildet $\mathbb {H}$ surjektiv auf $\mathbb {C}$ ab. Für Punkte $z,w\in {\mathbb {H}}$ gilt j(z)=j(w) dann und nur dann wenn es eine komplexe Zahl $a\in {\mathbb {C}}^{*}$ gibt, die das Gitter ${\mathbb {Z}}+z{\mathbb {Z}}$ auf das Gitter ${\mathbb {Z}}+w{\mathbb {Z}}$ überführt, also genau dann wenn die Quotienten ${\mathbb {C}}/({\mathbb {Z}}+z{\mathbb {Z}})$ und ${\mathbb {C}}/({\mathbb {Z}}+w{\mathbb {Z}})$ als elliptische Kurven isomorph sind. Sie parametrisiert also eindeutig die Elliptischen Funktionen. Sie liefert eine Bijektion $\mathbb {H} \backslash \Gamma \to \mathbb {C}$ . 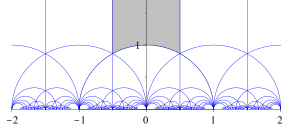Ihr Fundamentalbereich ist durch die Modulfigur gegeben (siehe Abbildung).

Ist $\tau$ ein Element aus einem quadratischen Zahlkörper mit positiven Imaginärteil, so ist $j(\tau )$ eine ganzalgebraische Zahl.

Jede Modulfunktion ist eine rationale Funktion der j-Funktion.

Fourierentwicklung

Die j-Funktion lässt sich in eine Fourierreihe entwickeln:

$j(\tau )={\frac 1q}+744+196884q+21493760q^{2}+864299970q^{3}+\ldots =\sum _{{n=-1}}^{\infty }c_{n}q^{n}$

mit $q={\mathrm e}^{{2\pi {\mathrm i}\tau }}.$

Alle Fourierkoeffizienten $c_{n}$ :

$1,744,196884,21493760,\dots$ (Folge

A000521 in OEIS)

sind natürliche Zahlen. Für ihr Wachstum gilt die asymptotische Formel

$c_{n}\cong {\frac {e^{{4\pi {\sqrt {n}}}}}{{\sqrt {2}}n^{{3/4}}}}$ ,

die 1932 von Petersson und unabhängig davon 1938 von Rademacher bewiesen wurde.

Die Fourierkoeffizienten sind Linearkombinationen der Dimensionen der irreduziblen Darstellungen der Monstergruppe mit kleinen ganzzahligen Koeffizienten. Dies folgt aus einer tiefen mathematischen Beziehung, die von McKay, Conway, Norton vermutet und von Richard Borcherds bewiesen wurde („monstrous moonshine“).

Literatur

Eberhard Freitag & Rolf Busam: Funktionentheorie 1, 4. Aufl., Springer, Berlin (2006), ISBN 3-540-31764-3
Max Koecher & Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer, Berlin (2007) ISBN 978-3-540-49324-2

Anmerkungen

↑ Das folgt daraus, dass im Zähler Eisensteinreihen stehen, die in diesem Grenzfall holomorph sind, und im Nenner die Diskriminante, die eine Spitzenform ist und eine einfache Nullstelle in dem betrachteten Grenzfall hat

Basierend auf einem Artikel in:

Wikipedia.de