
Halbwertsbreite
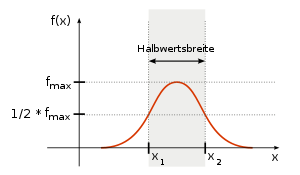
Die Halbwertsbreite einer Funktion mit einem Maximum ist die Differenz zwischen den beiden Argumentwerten, für die die Funktionswerte auf die Hälfte des Maximums abgesunken sind, anschaulich also die „Breite bei halber Höhe“.
Entsprechend ist im Englischen und in der Technik für die Halbwertsbreite die Bezeichnung FWHM (Full Width at Half Maximum) gebräuchlich. Ist die Funktion von der Zeit abhängig, wird die Abkürzung FDHM (Full Duration at Half Maximum) verwendet.
Definition
Eine Funktion
habe bei
ein Maximum. An den Stellen
und
ist der Wert der Funktion auf die Hälfte des Maximums abgesunken:
.
Dann ist die Halbwertsbreite die Differenz .
Umrechnung
Für eine feste Funktionsform kann man die Halbwertsbreite in anders
definierte Breiten der Funktion umrechnen. So kann man z.B. bei der Normalverteilung die
FWHM und die Standardabweichung
ineinander umrechnen:
Peakverbreiterung
Die Zunahme der Halbwertsbreite eines Peaks wird als Peakverbreiterung bezeichnet. Dabei bleibt die Intensität des Peaks (d.h. sein Integral über der Ausdehnungsgröße) meist gleich, dafür nimmt die Peakhöhe ab.
Mögliche Ursachen für eine Peakverbreiterung sind z.B. in der Physik die Linienverbreiterung (Emissionslinien zeigen energetische Verbreiterung) bzw. die Dispersion (Wellenpakete zerfließen mit der Zeit).
Anwendungsbeispiele
Antennen
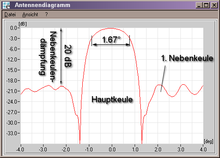
In der Antennentechnik wird der Richtfaktor einer Antenne als Halbwertsbreite (oder „Öffnungswinkel“) angegeben. Gemeint ist hier der Abstand zwischen den −3-dB-Grenzen. Die Halbwertsbreite der Antenne im nebenstehenden Beispiel ist also 1,67°.
Beleuchtung
Die Abstrahlcharakteristik einer Leuchte (mit Optik) wird meist vereinfacht mit einem Winkel angegeben. Dieser „Abstrahlwinkel“ ist ebenfalls der Halbwertswinkel, d.h. der volle Winkel zwischen den zwei Punkten einer Leuchtebene, an denen der Lichtstrom nur noch die Hälfte des Maximums erreicht. Bei dieser vereinfachten Angabe wird von einer zur Leuchtachse rotationssymmetrischen Lichtverteilungskurve ausgegangen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.02. 2022