
Peak
Der Begriff Peak kommt aus dem Englischen und bedeutet ‚Gipfel, Spitze, Scheitelwert‘. In der Messtechnik und Stochastik bezeichnet man mit Peak einen signifikanten Spitzenwert.
Zeichnet man Messwerte in einem Diagramm in senkrechter Richtung (Ordinate, y-Achse) gegen die Zeit, den Ort oder eine andere Größe (z.B. Wellenlänge) als waagerechte Achse (Abszisse, x-Achse) auf, stellen sich erhöhte Messwerte als Gipfel/Spitzen dar. Auch sie werden Peaks genannt. Bei ihnen ist einerseits der x-Wert des Maximums interessant, außerdem aber meist auch entweder die Scheitelhöhe oder die Fläche unter dem Peak. In der Praxis sind die Messwerte links und rechts vom Peak meist nicht Null, sondern der Peak ist ein deutlicher Anstieg und Wiederabfall (Ausschlag) des Messsignals über das Grundrauschen hinaus.
Beispiele:
- Chromatographie (Gaschromatographie, Hochleistungsflüssigkeitschromatographie): jeder Peak im Chromatogramm entspricht einer nachgewiesenen Substanz
- jeder „Photopeak“ in einem Gammaspektrum entspricht einer nachgewiesenen Gamma-Spektrallinie
- in der Wirtschaftsstatistik etwa Peak Oil, der Zeitpunkt des Ölfördermaximums
- in der Akustik und in der Audiotechnik nennt man die Peaks die Aussteuerung, und misst mit dem Aussteuerungsmesser (Peakmeter), das die maximale Spitze über eine Messperiode anzeigt
Maß für die Intensität des Peaks sind im Allgemeinen die Faktoren, die man auch bei Normalverteilung zugrunde legt, im Speziellen etwa Werte, die der Zeitbewertung des Peaks dienen:
- der Scheitelfaktor, ein Maß über das Verhältnis von Peakpegel zu Mittelwert (Effektivwert in der elektrischen Messtechnik)
bzw.
für negative Peaks bei nur-positiven Skalen, sonst
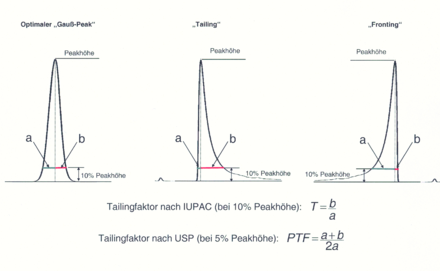
- der Tailingfaktor (‚Taillierung‘ der Spitze, Breite des Ausschlags), etwa bei 5 % oder 10 % der Peakhöhe, der auch ein Maß für die Symmetrie des Ausschlags ist
oder
mit ya, yb als Entfernung des zugrundeliegenden Prozentwerts von Spitzenwert


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.10. 2024
