
Flächenformel von Pappus
Die Flächenformel von Pappus, auch Satz des Pappus genannt, ist ein Lehrsatz der euklidischen Dreiecksgeometrie, der auf den spätantiken Mathematiker Pappus Alexandrinus zurückgeht und welcher von diesem in Buch IV der Mathematischen Sammlungen etwa im Jahr 320 vorgestellt wurde. Die Formel behandelt eine wesentliche Verallgemeinerung des Satzes des Pythagoras und gilt für beliebige Dreiecke, wobei Parallelogramme anstelle der pythagoreischen Quadrate treten.
Formulierung

Gegeben sei ein beliebiges Dreieck
der euklidischen
Ebene
.
Als Grundseite des Dreiecks sei
die dem Eckpunkt
gegenüberliegenden Dreiecksseite
gewählt.
Über den beiden anderen Dreiecksseiten
und
,
jeweils gegenüber den Eckpunkten
bzw.
,
seien zwei beliebige Parallelogramme
und
gelegen und dabei sei
der Schnittpunkt der beiden Geraden
und
[1] [2]
Über der Grundseite
liege das Parallelogramm
,
und dafür sei vorausgesetzt:
Dann gilt:
- Der Flächeninhalt
des Parallelogramms
ist gleich der Summe der Flächeninhalte der beiden Parallelogramme
und
.
- In Formeln:
Zum Beweisgang
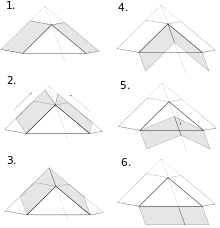
Der Beweisgang lässt sich so darstellen:[4]
Ausgangspunkt ist Tatsache, dass durch die Gerade
eine Aufteilung der euklidische Ebene
in zwei abgeschlossene
Halbebenen gegeben ist.[5]
Die Schnittmengen
dieser beiden Halbebenen mit dem Parallelogramm
bilden wiederum zwei Parallelogramme
und
,
welche
aufteilen, wobei
der Schnittpunkt der Geraden
mit der Seite
ist und
der Schnittpunkt der Geraden
mit der Seite
.
Mittels Scherung
und Parallelverschiebung
– in der jeweiligen Halbebene! – sieht man nun, dass
flächengleich ist mit
und ebenso
flächengleich mit
.
Dies lässt sich in drei Teilschritten (s. u.) nachvollziehen, wobei die
Behandlung der beiden Parallelogramme
und
vollkommen gleichartig ist.
Auf diesem Wege erhält man dann die gewünschte Identität:
.
Darstellung der Teilschritte
Anhand des Parallelogramms
lassen sich die Teilschritte wie folgt beschreiben:
- Teilschritt 1
Innerhalb des von den Geraden
und
berandeten
– also dazwischen liegenden! – abgeschlossenen
Streifens[6]
wird das Parallelogramm
in ein flächengleiches Parallelogramm geschert,
und zwar derart, dass die Punkte
der Seite
festbleiben,
während der Punkt
in den Punkt
,
der Punkt
in den Punkt
,
die Seite
in die Seite
und die Seite
in die Seite
übergehen.
- Teilschritt 2
Längs der Geraden
und dabei stets innerhalb des von den Geraden
sowie
berandeten abgeschlossenen Streifens
wird das in Teilschritt 1 entstandene Parallelogramm so verschoben, dass
ein neues Zwischenparallelogramm entsteht, wobei
in
und
in
übergehen.
- Teilschritt 3
Innerhalb
wird das in Teilschritt 2 entstandene Zwischenparallelogramm in das
Parallelogramm
geschert, und zwar derart, dass alle Punkte der Seite
festbleiben.
Zusammenhang mit dem Satz des Pythagoras
Der Satz des Pythagoras ergibt sich, wenn man annimmt, dass erstens das
Dreieck
rechtwinklig
ist mit rechtem Winkel bei
,
mit Katheten
bzw.
sowie Hypotenuse
und dass zweitens die Parallelogramme
und
Quadrate
sind.
Wie sich dann zeigt, sind die Dreiecke
und
beide rechtwinklig sowie zum Ausgangsdreieck
kongruent
und die Gerade
fällt mit der Höhengeraden
durch
auf
zusammen. Das Parallelogramm
ist daher ein Rechteck und wegen
sogar ein Quadrat. Die Flächenformel fällt folglich in diesem Falle mit der pythagoreischen
Formel
zusammen. Weiterhin zeigt sich, dass mit dem obigen Beweisgang zugleich auch ein Beweis des euklidischen Kathetensatzes gegeben ist.
Abgrenzung
Der hiesige Lehrsatz ist nicht identisch mit dem Großen Satz von Pappus, welcher allerdings ebenfalls auf Pappus Alexandrinus zurückgeht.
Literatur
- Claudi Alsina, Roger B. Nelsen: Bezaubernde Beweise: Eine Reise durch die Eleganz der Mathematik. Springer Spektrum, Berlin / Heidelberg 2013, ISBN 978-3-642-34792-4.
Anmerkungen
- ↑ Die Formulierung Über … bedeutet, dass das jeweilige Parallelogramm mit dem Dreieck nur eine Seite gemeinsam hat, also – ;in diesem Sinne! ;– außerhalb des Dreiecks liegt.
- ↑
Die Reihenfolge der Punkte ist für die
Darstellung der Geraden und Strecken unwesentlich. Es ist also für zwei Punkte
stets
und
.
- ↑ Eine Strecke ist parallel zu einer gegebenen Geraden genau dann, wenn die Gerade, auf der die Strecke liegt, und die gegebene Gerade parallel sind.
- ↑ Die Darstellung folgt im Wesentlichen der von Alsina und Nelsen (S. 92). Alsina und Nelsen geben an, ihre Darstellung sei wiederum von dem amerikanischen Mathematiker Howard Whitley Eves übernommen. Der Beweisansatz ähnelt dem des Scherungsbeweises des Pythagoreischen Lehrsatzes. Die im Lambacher-Schweizer auf S. 102 zu findende Skizze legt nahe, dass dieser Ansatz zum Beweis der Flächenformel schon früher bekannt war.
- ↑
ist also in die beiden zugehörigen offenen Halbebenen zerlegt.
- ↑
Geht man von einer festgelegten Links-Rechts-Orientierung
der euklidischen Ebene
aus und bezeichnet man für zwei verschiedene parallele Geraden
die abgeschlossenen Halbebenen auf der linken Seite mit
bzw.
, die auf der rechten Seite mit
bzw.
und nimmt man weiter o. B. d. A.
an, so hat der dazwischen liegende Streifen die Darstellung
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.01. 2022