Stromteiler

Der Stromteiler ist eine Parallelschaltung aus passiven elektrischen oder magnetischen Zweipolen, durch die ein elektrischer Strom bzw. ein magnetischer Fluss in mehrere Teilströme/-flüsse aufgeteilt wird.

Stromteiler für Wechselstrom können auch mit Transformatoren realisiert werden, sie heißen dann Stromwandler.

Allgemeine Stromteilerregel

Zur einfachen Berechnung der Teilströme bietet sich die Stromteilerregel an. Diese Regel gilt nur, wenn alle Zweige, auf die sich der Gesamtstrom aufteilt, passiv sind. Bei Gleichstrom sind dies ohmsche Widerstände. Bei Wechselstrom wären zusätzlich Kondensatoren (kapazitiver Stromteiler) und Spulen (induktiver Stromteiler) möglich. In magnetischen Schaltungen gibt es nur magnetische Widerstände. Sobald aktive Bauelemente wie Quellen vorkommen, muss auf das Maschenstromverfahren zurückgegriffen werden. Anwendung findet die Stromteilerregel auch bei Berechnung eines Netzwerkes mit Hilfe des Überlagerungsverfahrens.

Die Stromteilerregel lautet:

${\frac {{\text{Teilstrom}}}{{\text{Gesamtstrom}}}}={\frac {{\text{Gesamtwiderstand}}}{{\text{Vom Teilstrom durchflossener Widerstand}}}}$

oder mit Leitwerten ausgedrückt:

${\frac {{\text{Teilstrom}}}{{\text{Gesamtstrom}}}}={\frac {{\text{Vom Teilstrom durchflossener Leitwert}}}{{\text{Gesamtleitwert}}}}$

mit

${\text{Leitwert}}={\frac {1}{{\text{Widerstand}}}}$

Stromteiler mit ohmschen Widerständen

Verallgemeinert auf n parallele Zweige (i = 1…n) ergeben sich für den Strom in Zweig k:

für ohmsche Schaltungen

${\frac {I_{k}}{I}}={\frac {R}{R_{k}}}={\frac {G_{k}}{G}}$

mit dem Gesamtwiderstand ${\frac {1}{R}}=\sum _{{i=1}}^{n}{\frac {1}{R_{i}}}$ und dem Gesamtleitwert $G=\sum _{{i=1}}^{n}G_{i}$

für komplexe Schaltungen

${\frac {I_{k}}{I}}={\frac {Z}{Z_{k}}}={\frac {Y_{k}}{Y}}$

mit der Gesamtimpedanz ${\frac {1}{Z}}=\sum _{{i=1}}^{n}{\frac {1}{Z_{i}}}$ und der Gesamtadmittanz $Y=\sum _{{i=1}}^{n}Y_{i}$

für magnetische Schaltungen

${\frac {\Phi _{k}}{\Phi }}={\frac {R_{m}}{R_{{m_{k}}}}}={\frac {G_{{m_{k}}}}{G_{m}}}$

mit dem Gesamtwiderstand ${\frac {1}{R_{m}}}=\sum _{{i=1}}^{n}{\frac {1}{R_{{m_{i}}}}}$ und dem Gesamtleitwert $G_{m}=\sum _{{i=1}}^{n}G_{{m_{i}}}$

Die Widerstände eines jeden Zweiges müssen zunächst zu einem Widerstand pro Zweig zusammengefasst werden, um den Gleichungen in der oben abgebildeten Form zu entsprechen. Der Gesamtwiderstand bezieht sich nur auf die betrachtete Parallelschaltung, in der sich der Gesamtstrom aufteilt. Eventuelle Widerstände, die vor oder nach der Parallelschaltung in Reihe liegen, werden nicht berücksichtigt. Bei komplexeren Schaltungen mit mehrfachen Verzweigungen, muss die Formel eventuell mehrmals angewendet werden, um den gesuchten Teilstrom zu erhalten.

Zur groben Kontrolle der mit dieser Regel berechneten Ströme eignen sich zwei einfache Merksätze. Zum einen ist jeder Teilstrom kleiner als der Gesamtstrom, da dieser der Summe aller Teilströme entspricht. Zum anderen verhalten sich die Teilströme in den Zweigen umgekehrt proportional zu ihren Zweigwiderständen. Das bedeutet, je kleiner (größer) der Zweigwiderstand ist, desto größer (kleiner) ist der Teilstrom.

In manchen Quellen wird die Regel etwas modifiziert ausgedrückt. Anfangs wirkt diese Variante etwas schwieriger, doch fällt sie geübten Anwendern mit der Zeit ebenso leicht wie die erste Variante. Sie lautet folgendermaßen:

${\frac {{\text{Teilstrom}}}{{\text{Gesamtstrom}}}}={\frac {{\text{Vom Teilstrom nicht durchflossener Teilwiderstand}}}{{\text{Ringwiderstand der Masche}}}}$

Herleitung der Regel für ein einfaches Beispiel

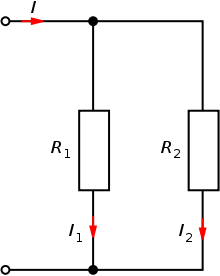
Stromteiler aus zwei parallel geschalteten ohmschen Widerständen

Laut den Kirchhoffschen Regeln teilt sich der Gesamt-Strom $\,I$ auf die beiden Zweige auf:

$\,I=I_{1}+I_{2}$

Da über den beiden parallel geschalteten Widerständen die gleiche Spannung abfällt, gilt nach dem ohmschen Gesetz:

$U=R_{1}\cdot I_{1}=R_{2}\cdot I_{2}$

Löst man diese Gleichung nach $I_{2}$ auf

$I_{2}={\frac {R_{1}}{R_{2}}}\cdot I_{1}$

und setzt das Ergebnis in $I=I_{1}+I_{2}$ ein, ergibt sich:

$I=I_{1}\cdot \left(1+{\frac {R_{1}}{R_{2}}}\right)=I_{1}\cdot {\frac {R_{1}+R_{2}}{R_{2}}}=I_{1}\cdot {\frac {R_{1}+R_{2}}{R_{2}}}\cdot {\frac {(R_{1}\cdot R_{2})}{(R_{1}\cdot R_{2})}}=I_{1}\cdot {\frac {R_{1}}{R_{1}\parallel R_{2}}}$

Dividiert man durch $I_{1}$ und bildet auf beiden Seiten den Kehrwert, ergibt sich dasselbe Ergebnis wie für die Stromteilerregel:

${\frac {I_{1}}{I}}={\frac {R}{R_{1}}}$ und für den anderen Zweig ${\frac {I_{2}}{I}}={\frac {R}{R_{2}}}$ mit dem Gesamtwiderstand $R=R_{1}\parallel R_{2}$

Der Gesamtstrom sowie die Werte der Widerstände sind im Allgemeinen bekannt.

Beispiel mit Mehrfach-Anwendung

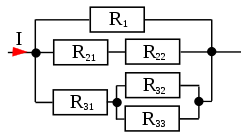
Stromteiler aus drei Zweigen mit einer inneren Verzweigung im untersten Zweig

Gesucht wird der Strom durch $R_{{32}}$ . Dazu wird zunächst der Strom $I_{3}$ im untersten Zweig berechnet. Die Stromteilerregel ergibt die Gleichung:

${\frac {I_{3}}{I}}={\frac {R_{1}\parallel R_{2}\parallel R_{3}}{R_{3}}}$

mit $\,R_{2}=R_{{21}}+R_{{22}}$ und $R_{3}=R_{{31}}+\left(R_{{32}}\parallel R_{{33}}\right)$

Der Teilstrom $I_{3}$ fließt durch die Parallelschaltung aus $R_{{32}}$ und $R_{{33}}$ . Durch nochmalige Anwendung der Stromteilerregel, wird der Strom durch $R_{{32}}$ abhängig von $I_{3}$ ermittelt:

${\frac {I_{{32}}}{I_{3}}}={\frac {R_{{32}}\parallel R_{{33}}}{R_{{32}}}}$

Werden beide Gleichungen miteinander multipliziert, ergibt sich eine Gesamtgleichung, in der $I_{{32}}$ direkt von I abhängig ist:

${\frac {I_{3}}{I}}\cdot {\frac {I_{{32}}}{I_{3}}}={\frac {I_{{32}}}{I}}={\frac {R_{1}\parallel R_{2}\parallel R_{3}}{R_{3}}}\cdot {\frac {R_{{32}}\parallel R_{{33}}}{R_{{32}}}}$

Beispiel für magnetischen Kreis

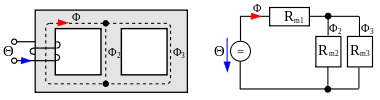
magnetischer Flussteiler aus zwei Zweigen

In magnetischen Schaltungen wird die Regel genauso angewendet. Für die Teilflüsse durch $R_{{m_{2}}}$ und $R_{{m_{3}}}$ ergeben sich die Gleichungen:

${\frac {\Phi _{2}}{\Phi }}={\frac {R_{m_{23}}}{R_{m_{2}}}}$ und für den anderen Zweig ${\frac {\Phi _{3}}{\Phi }}={\frac {R_{m_{23}}}{R_{m_{3}}}}$ mit dem Gesamtwiderstand der Parallelschaltung $R_{m_{23}}=R_{m_{2}}\parallel R_{m_{3}}$

Anwendung

Stromteiler werden insbesondere zur Messung hoher Ströme verwendet, sie heißen dann Shunt, wobei das Messgerät einen der Strompfade bildet. Im Wesentlichen misst es jedoch die am Hauptpfad abfallende Spannung, da es nur von einem sehr kleinen Teilstrom durchflossen wird. In Vielfachmessgeräten befinden sich umschaltbare Stromteiler zur Strommessung in verschiedenen Bereichen.

Siehe auch

Spannungsteiler

Basierend auf einem Artikel in:

Wikipedia.de