Konstantstromquelle
Eine Konstantstromquelle realisiert innerhalb sehr kleiner Abweichungen die ideale Stromquelle, die einen konstanten elektrischen Strom in einen Stromkreis einspeist, unabhängig von der elektrischen Spannung an ihren Anschlusspunkten und von der Ausführung des weiteren Stromkreises. Der abgegebene Strom wird auch als eingeprägter Strom bezeichnet. Die Einschränkung gegenüber dem Modell der idealen Stromquelle besteht in der nur begrenzt abgebbaren Spannung.
Prinzipielles
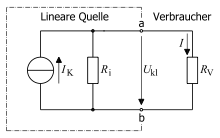
Nebenstehendes Bild zeigt eine reale Stromquelle mit dem Innenwiderstand
.
Bei einer idealen Konstantstromquelle entfällt der eingezeichnete
Innenwiderstand, weil gilt:
(zwischen zwei beliebigen Punkten einer Schaltung vorhandene unendlich große
Widerstände werden nicht eingezeichnet), d.h. es liegt ein möglichst
hoher, idealerweise unendlicher Differentieller
Widerstand der Quelle vor. Der Verbraucherstrom;
ist idealerweise unabhängig von
.
Damit dieser wirklich fließt, baut die Quelle eine passend hohe elektrische
Spannung
zwischen den Klemmen a und b auf – bei einem ohmschen Verbraucher
also
Es gibt auch Konstantstromquellen für Wechselstrom, beispielsweise müssen transformatorische Stromwandler so behandelt werden. Der Eisen-Wasserstoff-Widerstand ist ein historisches Beispiel einer für alle Stromarten geeigneten Konstantstromquelle, auch Kompensationsstromwandler sind dazu in der Lage. Labornetzteile im Strombegrenzungsmodus oder Messumformer mit Stromsignal (Stromschnittstelle, z.B. 4–20-mA-Schleife) sind Beispiele für Gleichstromquellen.
Gleichstromquellen sind elektronische Schaltungen, die ausschließlich Gleichstrom liefern
können – die Ausgangsspannung kann jedoch eine lastbedingte überlagerte
Wechselspannung aufweisen. Typische Realisierungen werden nachfolgend
vorgestellt. Die Spannung, die am Verbraucher aufgebaut werden kann, ist bei
diesen Schaltungen begrenzt auf ein ,
ein Wert, der kleiner bleibt als die Speisespannung der Schaltung. Neben dem
Maximalwert des Stromes, den die Schaltung liefern kann, ist ein Maximalwert von
zu beachten, bis zu dem sie bestimmungsgemäß arbeiten kann:
Beispiel: Kann die Schaltung an den Klemmen eine Spannung
= 12 V aufbauen bei einem Strom
= 20 mA, so darf die Bürde betragen
Schaltungen von Gleichstromquellen
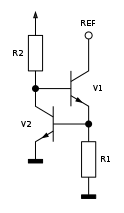
Mit Bipolartransistor
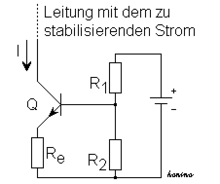
Eine Konstantstromquelle kann im einfachsten Fall durch einen gegengekoppelten
Bipolartransistor
realisiert werden. Die Basis wird durch einen Spannungsteiler
aus den Widerständen
und
auf einer konstanten Spannung gehalten. Der Transistor wird hierdurch leitend
und führt einen gewissen Strom
,
der durch den Emitterwiderstand
fließt, und an ihm nach dem ohmschen
Gesetz eine Spannung
hervorruft. Mit steigendem
würde zugleich
ansteigen. Damit wird aber der Emitter in seiner Spannung gegenüber der Basis
angehoben, wodurch die Basis-Emitter-Spannung
sinkt. Dies steuert den Transistor zu und lässt den Strom sofort wieder sinken.
Würde sich andererseits
verkleinern, so wird die Spannung
am Emitterwiderstand kleiner und damit die Basis-Emitter-Spannung größer,
wodurch sich der Kollektorstrom wieder erhöht. Diesen Vorgang der Stabilisierung
nennt man auch Gegenkopplung,
wodurch der ohnehin bereits relativ hohe Ausgangswiderstand
des Transistors weiter vergrößert wird
(siehe Bipolartransistor#Kennlinienfelder).
Da über der Basis-Emitter-Strecke stets eine Spannung von ca. 0,7 V bei
Silizium-Transistoren abfällt, stellt sich der Strom immer so ein, dass
um 0,7 V kleiner als die an
anliegende Spannung ist. Durch die Wahl von
oder durch die Spannung an
kann also der gewünschte Strom eingestellt werden.
Nachteilig ist die starke Abhängigkeit von Temperatur und herstellungsbedingten Exemplarstreuungen. Die weiter unten beschriebenen Schaltungen zielen genau auf eine Vermeidung dieser Schwachstellen, was durch eine gewisse Symmetrie des Schaltungsaufbaus erreicht wird (Temperaturkompensierte Konstantstromquelle).
Mit Feldeffekttransistor
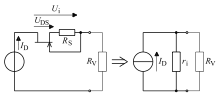
Eine Konstantstromquelle kann mittels eines Feldeffekttransistors
mit (oder auch ohne) Source-Widerstand
wie in nebenstehendem Bild aufgebaut werden. Es entsteht ein von
abhängiger Spannungsabfall
,
der sich wie bei einem Quellenwiderstand
einstellt. Der differentielle
Widerstand liegt in der Größenordnung 1 MΩ.
Solche Schaltungen werden als Stromregeldiode bezeichnet und sind als fertige Bauelemente erhältlich.
Mit Operationsverstärker
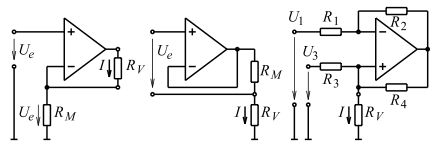
Die gezeigten Beispiele sind Spannungs-Strom-Umformer. Aufgrund einer Eingangsspannung entsteht ein Strom, der unabhängig vom Verbraucher ist. Zum Verständnis werden die mit sehr guter Näherung geltenden zwei Generalregeln für den nicht übersteuerten Operationsverstärker genannt:
- Keine Spannung zwischen den Eingängen,
- Kein Strom in die Eingänge.
- Linke Schaltung:
Der Strom ist unabhängig vom Verbraucherwiderstand, solange die Spannung an
kleiner ist als die vom Operationsverstärker an seinem Ausgang maximal
lieferbare Spannung. Die Spannung
liegt am Bezugspotential (Masse); der Verbraucher muss potentialfrei sein. Das
sind dieselben Randbedingungen wie oben beim Bipolartransistor.
- Mittlere Schaltung:
Wie bei der linken Schaltung fällt
an
ab. Allerdings muss hier
potentialfrei sein; der Verbraucher liegt an Masse.
- Rechte Schaltung:
wenn
. Hier liegen
,
und
an Masse.
Mit integrierten Schaltkreisen

Es gibt zweipolige Konstantstromquellen als Integrierte Schaltung (IC) für verschiedene Ströme im Milliampere-Bereich. Weiterhin gibt es LED-Treiber-IC, die eine oder mehrere, oft steuerbare Konstantstromquellen besitzen. Solche Schaltkreise arbeiten analog oder als Schaltregler. Im letzteren Fall benötigen sie eine externe Speicherdrossel.
Konstantstromquellen lassen sich auch mit integrierten Längsregler-Schaltkreisen realisieren, indem man deren innere Referenzspannung zur Strommessung an einem Shunt (Strommesswiderstand) nutzt. Die Schaltung ist ähnlich der mit einem Feldeffekttransistor. Die Referenzspannung des LM317 beträgt z.B. 1,25 Volt – der Schaltkreis stellt den Strom so ein, dass genau diese Spannung am Shunt abfällt. Der Vorteil ist der gegenüber Bipolartransistoren geringe Steuerstrom und die hohe Belastbarkeit, daher sind solche Lösungen auch für größere Ströme im Ampere-Bereich geeignet. Nachteile sind der recht hohe Gesamt-Spannungsabfall, der sich aus der Summe der Spannung am Shunt (1,25 V) und der Spannung am Schaltkreis (engl. drop, beim LM317 bei 1 A ca. 2 V) ergibt, sowie der kleine, allerdings nahezu konstante Querstrom der Längsregler (bis 0,1 mA, der sich zum errechneten Ausgangsstrom addiert.
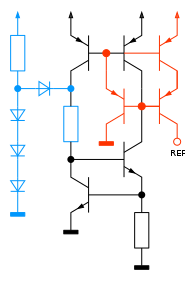
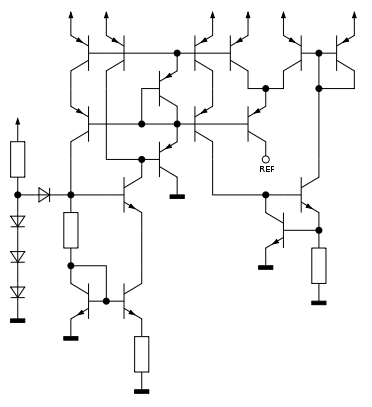
PTAT-Stromquelle
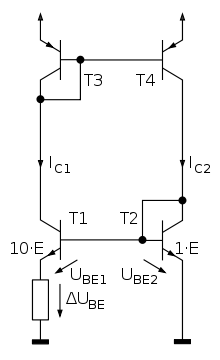

IS2 = 1 · 10−15 A
n = 10
R3 = 100 Ω
UT = 25,9 mV
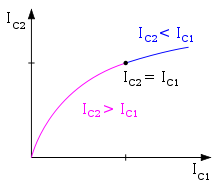
Die PTAT-Stromquelle liefert einen Strom, der sich proportional zur absoluten Temperatur ändert (PTAT = proportional to absolute temperature). In der nebenstehenden Schaltung bilden T3 und T4 einen idealen Stromspiegel sowie T1 und T2 einen nicht perfekten Stromspiegel. Bei gleicher Basis-Emitter-Spannung sei der Emitterstrom von T1 größer als der von T2, was zum Beispiel durch Parallelschaltung mehrerer Transistoren zu erreichen ist. Die Strom-Spannungs-Kennlinie im Bild darunter zeigt das Verhalten der Kollektorströme von T1 und T2 in Abhängigkeit von der Basis-Emitter-Spannung UBE2. Durch die lineare Gegenkopplung des exponentiellen Kennlinienverlaufs mit dem Widerstand R1 übertrifft bei höherer Basis-Emitter-Spannung UBE2 der Emitterstrom des Transistors T2 denjenigen von T1. Im Schnittpunkt der Kennlinien tritt eine exakte Stromspiegelung auf. Die Verbindung mit dem Stromspiegel T3+T4 führt zu einem stabilen Arbeitspunkt mit konstantem Strom.
Sinkt der Kollektorstrom IC2 und die Basis-Emitter-Spannung UBE2 unter den Arbeitspunkt USchnitt dann ist der Kollektorstrom IC1 größer als IC2. Der Stromspiegel aus T3 und T4 kopiert den Stromanstieg von IC1 auf IC2 wodurch UBE2 steigt bis der Arbeitspunkt erreicht wird. Oberhalb des Schnittpunktes steigt nun IC2 verglichen mit IC1 schneller und die Basisspannung wird heruntergeregelt. Die Schaltung regelt die beiden Ströme gleich aus, also IC1 = IC2.
Der Strom im Arbeitspunkt lässt sich wie folgt berechnen:
Aus der Großsignalgleichung des Bipolartransistors
ergibt sich durch Auflösung nach der Basis-Emitter-Spannung
.
Die unterschiedlichen Eigenschaften der Transistoren T1 und T2 seien durch
das Verhältnis
der Sperrströme charakterisiert
.
Die Spannung am Emitterwiderstand ist somit
Aus
und wegen der Gleichheit der Kollektorströme
resultiert zusammengefasst und gekürzt die Formel:
In die Gleichung für den Strom
eingesetzt ergibt das:
Der Strom weist eine direkte Abhängigkeit von der absoluten Temperatur auf. Durch mehrfache Anzapfung am oberen Stromspiegel kann aus dem Strom IC1 der Referenzstrom gewonnen werden.
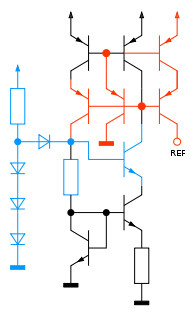
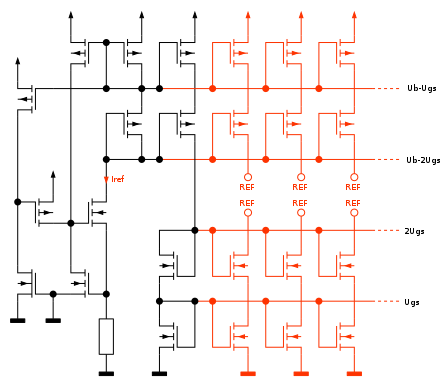
UBE-Konstantstromquelle
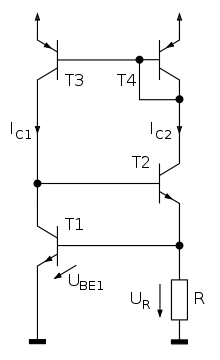
Die UBE-Konstantstromquelle liefert das Gegenstück zur PTAT-Konstantstromquelle, da deren Temperaturkoeffizient einen negativen Wert aufweist und über einen großen Temperaturbereich als konstant anzusehen ist.
In der nebenstehenden Schaltung bilden T1, T2 und R einen „unperfekten“ Stromspiegel von IC1 nach IC2 sowie T3 und T4 einen idealen Stromspiegel von IC2 nach IC1.
Betrachtet wird nun der untere Stromspiegel. Fließt ein Strom IC1 regelt T2 solange bis sich an R und somit UBE1 eine Spannung einstellt mit der der gesamte Strom von IC1 über T1 abfließt. Der Basisstrom der Transistoren ist vernachlässigbar gering und bleibt daher unberücksichtigt. Weiter ergibt sich aus dem Spannungsabfall am Widerstand unmittelbar der Strom IC2.
Zusammen mit dem oberen Stromspiegel entsteht ein Regelkreis mit einem stabilen Arbeitspunkt bei IC1 = IC2. Liegt der Strom IC1 unterhalb des Arbeitspunktes liefert der untere Stromspiegel einen höheren Strom IC2 im Verhältnis zu IC1. Diese Erhöhung führt über den oberen Stromspiegel zur Erhöhung von IC1 solange bis der Arbeitspunkt erreicht ist. Liegt der Strom IC1 oberhalb des Arbeitspunktes liefert der untere Stromspiegel einen niedrigeren Strom IC2 im Verhältnis zu IC1. Diese Reduzierung führt über den oberen Stromspiegel zur Reduzierung von IC1 solange bis der Arbeitspunkt erreicht ist.
Bei gegebenem Transistorparameter IS1 und der Vorgabe eines gewünschten Stroms Iref errechnet sich der Widerstand folgendermaßen:
Die Temperaturabhängigkeit verhält sich proportional zum Temperaturkoeffizienten von UBE1 bei Annahme die Änderung von IC1 sei vernachlässigbar (IC1 = konst), dann gilt:
- M … Herstellungsparameter, Wertebereich −1,0 bis −1,5
- UG … Bandabstandsspannung von Silizium (UG(300 K) = 1,12 V)
Durch mehrfache Anzapfung am oberen Stromspiegel kann aus dem Strom IC1 der Referenzstrom gewonnen werden.
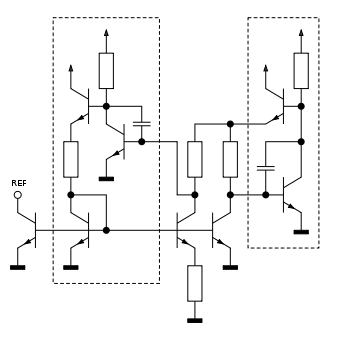
Temperaturkompensierte Konstantstromquelle
Durch geeignete Kombination von PTAT- und UBE-Stromquelle entsteht eine temperaturkompensierte Konstantstromquelle. Auf einem vergleichbaren Konzept beruht die Bandabstandsreferenz.
Da die PTAT- und die UBE-Stromquelle überwiegend aus Transistoren und nur wenigen Widerständen bestehen, eignen sich beide Schaltungen sehr gut für integrierte Schaltkreise. Für einen diskreten Schaltungsaufbau ist ein Transistorarray notwendig, weil zwischen den Transistoren T1 und T2 sowie T3 und T4 eine gute thermische Kopplung bestehen muss.
Realisierung
| |||
| |||
| |||
|
Anwendung
- Versorgung von Leuchtdioden (LED) und Laserdioden, siehe Betrieb und Anschluss von LEDs
- Arbeitspunktregelung im Operationsverstärker und anderen integrierten Schaltkreisen.
- Messung großer Kapazitätswerte (z. B. Elektrolytkondensatoren)
- Stromschnittstellen


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.05. 2024