Black Box (Systemtheorie)

Schema einer Black Box

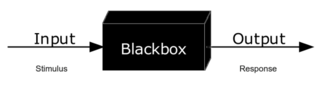
Als Black Box bezeichnet man in Kybernetik und Systemtheorie ein (möglicherweise sehr komplexes) System, von welchem im gegebenen Zusammenhang nur das äußere Verhalten betrachtet werden soll. Die innere Struktur mag bekannt sein; solche Kenntnis darf aber nicht benutzt werden (etwa weil ein Nachfolgemodell innen anders gebaut sein darf). Man beschränkt sich bei der Untersuchung und Beschreibung auf die Messung der Input-Output-Beziehungen (EVA-Prinzip).

Anders als ein geschlossenes System in der Thermodynamik darf so ein System auch Materie mit der Umgebung austauschen, zum Beispiel ein Fahrscheinautomat.

Das Gegenteil einer Black Box wird meistens als White Box (engl. für weiße Kiste) bezeichnet; die metaphorisch konsistenteren Begriffe Glass Box und Clear Box (engl. für Glaskiste bzw. durchsichtige Kiste) sind synonym, werden aber seltener verwendet.

Wortherkunft

Der Begriff Black Box (engl. für schwarze Kiste) stammt ursprünglich aus der militärischen Fernmeldetechnik und bezeichnete erbeutetes Feindgerät, das wegen der möglicherweise darin enthaltenen Sprengladung nicht geöffnet werden durfte.

Übersicht

Allgemein ist eine Black Box ein Objekt, dessen innerer Aufbau und innere Funktionsweise unbekannt sind oder als nicht von Bedeutung erachtet werden. Von Interesse ist vielmehr nur das Verhalten der Black Box, die über definierte Schnittstellen eine bestimmte Funktionalität sicherstellt. Die Motivation bei der Verwendung des Begriffs tendiert zu das Innere interessiert (jetzt) nicht, auch wenn er manchmal im Sinn von wir wissen es (sowieso) nicht verwendet wird. Diese Herangehensweise wird oft verwendet, um die Komplexität des Beobachtungsgegenstandes zu reduzieren. Das bewusste Weglassen von detaillierterer Information (Tiefeninformation) wird auch als Geheimnisprinzip bezeichnet. Der Systembearbeiter erhält dadurch einen energetischen Vorteil, den er für andere (theoretische und praktische) Belange verwenden kann.

"The only conceivable way of unveiling a black box, is to play with it" ("Der einzig denkbare Weg, um das Innere einer Black Box aufzudecken, ist, damit zu spielen.") René Thom, Mathematical Models, S. 298.

In der Systemtheorie wird die Black-Box-Betrachtungsweise methodisch eingesetzt, indem zur Analyse des Systemverhaltens lediglich die Beziehung zwischen Reiz bzw. Input und Reaktion bzw. Output analysiert wird. Kausalität ist dabei nicht vorausgesetzt, sondern eine vereinfachende Annahme. Idealerweise erlaubt die mathematische Beschreibung dieser Beziehungen Rückschlüsse auf das Substrat und die Art der Verschaltungen der Signale innerhalb des Systems.

Anwendung

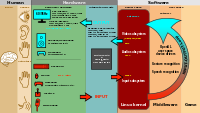
Beispiel: Die umfangreichen ICs werden als Black Box dargestellt, es wird nur die Ein- und Ausgabe betrachtet

Typische Form des Black-Box-Modells ist die Modularisierung.

Erfolgreich angewendet wird diese Methode bei elektronischen Schaltkreisen, neuronalen Systemen oder Einzelneuronen. Als Eingangsreize werden analytisch leicht analysierbare Signalformen wie z.B. sinusoidale Signale gewählt. Als Zwischenstadium der Analyse werden so genannte Ersatzschaltbilder konstruiert, in denen verschiedene elektronische Filter dem Systemverhalten entsprechend miteinander verschaltet werden. Daneben findet die Methode in zahlreichen numerisch-mathematischen Verfahren Anwendung.

Datenkapselung in der Programmierung und der Black-Box-Test bei der Software-Entwicklung sind Methoden der Softwareentwicklung.

Aus Sicht der organisatorischen Verantwortlichkeit wird von einer Black Box gesprochen, um etwa zu verdeutlichen, dass ein Wartungstechniker für gewisse innere Funktion eines Bauteils nicht zuständig ist – im Falle des Versagens soll es nur im Ganzen ausgetauscht werden.

Bei der Modellierung eines mathematischen Modells wird von einer Black Box gesprochen, wenn nicht das innere Verhalten eines Systems bei der Modellierung berücksichtigt werden soll, sondern lediglich die Reaktion eines Systems in einer mathematischen Formel beschrieben wird.

Basierend auf einem Artikel in:

Wikipedia.de