Magnetische Feldstärke

Name

Magnetische Feldstärke

${\vec {H}}$

Größen- und Einheitensystem	Einheit	Dimension
SI	A·m⁻¹	I·L⁻¹
Gauß (cgs)	Oe	L^−1/2·M^1/2·T⁻¹

Die magnetische Feldstärke (Formelzeichen: ), auch als magnetische Erregung bezeichnet, ordnet als vektorielle Größe jedem Raumpunkt eine Stärke und Richtung des durch die magnetische Spannung erzeugten Magnetfeldes zu. Sie hängt über die Materialgleichungen der Elektrodynamik (innerhalb linearer, homogener, isotroper, zeitinvarianter Materie zu: $\vec{B} = \mu \cdot \vec{H}$ ) mit der magnetischen Flussdichte ${\vec {B}}$ zusammen.

Die SI-Einheit der magnetischen Feldstärke ist Ampere pro Meter:

$\left[ H \right] = \,{\mathrm{A} \over \mathrm{m}}$

Verschiedene Leiteranordnungen

Gerader Leiter

Bei einem geraden Leiter ist die Feldstärke entlang einer kreisförmigen Feldlinie konstant. Wenn die magnetische Feldstärke außerhalb eines stromdurchflossenen geraden Leiters im Abstand bezeichnet, die Stromstärke im Leiter und den Radius der kreisförmigen Feldlinie, dann ist der Betrag der magnetischen Feldstärke in Material mit homogener magnetischer Permeabilität:

$H = \frac{I}{2 \pi \cdot r}$

Zahlenbeispiel: Im Abstand von 5 cm von der Achse eines geraden Leiters, welcher einen Strom von 50 A führt, beträgt die magnetische Feldstärke:

$H={\frac {I}{2\pi \cdot r}}={\frac {50\,\mathrm {A} }{2\pi \cdot 0{,}05\,\mathrm {m} }}=159{,}15\,\mathrm {\frac {A}{m}}$

Stromdurchflossener Ring

Wird eine einzige Windung mit dem Radius vom Strom durchflossen (Leiterschleife), misst man auf einem Punkt auf der Spulenachse im Abstand vom Mittelpunkt des Ringes die Feldstärke

$H={\frac {I\cdot r^{2}}{2(x^{2}+r^{2})^{3/2}}}$

Für die Herleitung siehe: Biot-Savart – Kreisförmige Leiterschleife

Zylinderspule

Magnetfeld einer Zylinderspule (im Querschnitt). Die Drahtwicklungen sind durch „×“ (Strom fließt in die Bildebene hinein) und „·“ (Strom fließt aus der Bildebene heraus) markiert.

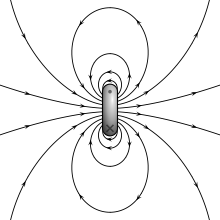
Wird eine Spule der Länge mit Durchmesser und Windungen vom Strom durchflossen, misst man im Zentrum die Feldstärke

$H = \frac{I \cdot N}{\sqrt{l^2 + D^2}}$

Handelt es sich um eine langgestreckte Spule (Länge viel größer als Durchmesser, für kurze Spulen existieren nur Näherungsformeln), kann man obige Formel vereinfachen und erhält:

$H = \frac {I \cdot N} {l} = \frac {U_m} {l} = \frac {\Theta} {l}$

Das Produkt $I\cdot N$ wird auch Amperewindungszahl oder als magnetische Spannung $U_{m}$ bezeichnet, die magnetische Spannung – durch historisch bedingte Begriffsbildung – auch als magnetische Durchflutung mit dem Formelzeichen $\Theta$ .

Entlang der Spulenachse ist an den Enden der Spule genau halb so groß wie in der Mitte. Im Innenraum der Spule ist fast unabhängig vom Abstand zur Spulenachse und annähernd homogen. Starke Abweichungen misst man erst an den Enden der Spule.

Helmholtz-Spule

Helmholtz-Spulenpaar

Zwei kurze, runde, hinsichtlich Größe und Windungszahl baugleiche und in gleicher Umlaufrichtung durchströmte Spulen im Abstand ihres Radius bauen zwischen sich ein weitgehend homogenes Magnetfeld auf. In der Mitte dieser als Helmholtz-Spule bekannten Anordnung hat das Magnetfeld die Feldstärke

$H={\frac {8\,N\,I}{R{\sqrt {125}}}}$ .

Dabei ist die Anzahl der Windungen (pro Spule).

Zusammenhänge mit anderen Größen

Aus den Materialgleichungen der Elektrodynamik ergibt sich der Zusammenhang zwischen der magnetischen Feldstärke und der magnetischen Flussdichte innerhalb linearer, homogener, isotroper, zeitinvarianter Materie in vektorieller Schreibweise:

${\vec {H}}={\vec {B}}\cdot {1 \over \mu }$ ,

wobei $\mu$ die magnetische Leitfähigkeit (Permeabilität) des betrachteten Raumpunktes ausdrückt. Allgemein gilt der Zusammenhang:

${\vec {B}}=\mu _{0}{\vec {H}}+{\vec {J}}$ ,

mit der magnetischen Polarisation $\vec{J}$ (nicht zu verwechseln mit der elektrischen Stromdichte, die traditionell ebenfalls mit $\vec{J}$ bezeichnet wird). Sofern die magnetische Polarisation ausschließlich durch die magnetische Feldstärke ${\vec {H}}$ erzeugt wird, gilt:

${\vec {J}}=\mu _{0}\chi _{m}{\vec {H}}$ ,

mit der magnetischen Suszeptibilität $\chi _{m}$ .

Innerhalb linearer, homogener, isotroper, zeitinvarianter Materie gilt folglich:

${\vec {B}}=\mu _{0}{\vec {H}}+{\vec {J}}=\mu _{0}{\vec {H}}+\mu _{0}\chi _{m}{\vec {H}}=\mu _{0}\left(1+\chi _{m}\right){\vec {H}}=\mu _{0}\mu _{m}{\vec {H}}=\mu {\vec {H}}$ ,

wobei $\mu$ den magnetischen Permeabilitätstensor beschreibt, der in vielen Fällen als Skalar angenommen wird.

Beziehung zur elektrischen Stromdichte $\vec{J}$

Die Beziehung

$\operatorname{rot}\ \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}$

aus den Maxwellschen Gleichungen stellt die lokale Form des Durchflutungssatzes dar. Dabei drückt $\vec{J}$ die elektrische Stromdichte und der zweite Summand mit der zeitlichen Ableitung der elektrischen Flussdichte ${\vec {D}}$ die Dichte des Verschiebungsstromes aus. Im einfachen statischen Fall ohne zeitliche Änderung verschwindet der zweite Summand und es gilt:

$\operatorname{rot}\ \vec{H} = \vec{J}$ .

Dies bedeutet, dass die Wirbeldichte des magnetischen Feldes ${\vec {H}}$ in jedem Raumpunkt gleich der lokalen Leitungsstromdichte ist. Die Bedeutung liegt darin, dass damit die Quellenfreiheit des magnetischen Feldes mathematisch ausgedrückt wird und die magnetischen Feldlinien immer in sich geschlossen sind.

Im Harmonisch eingeschwungenen Zustand (HZE) genügt die Betrachtung der Fouriertransformierten des Ampereschen Gesetzes:

$\operatorname {rot} \ {\vec {H^{*}}}={\vec {J^{*}}}+j\omega {\vec {D^{*}}}=\kappa ^{*}{\vec {E^{*}}}+j\omega \varepsilon ^{*}{\vec {E^{*}}}=j\omega \left(\varepsilon ^{*}-{\frac {\kappa ^{*}}{\omega }}j\right){\vec {E^{*}}}$ ,

$\varepsilon^*$ ist die komplexe elektrische Permittivität, die elektrische Relaxationsprozesse bzw. dielektrische Verluste im Material berücksichtigt. $\kappa ^{*}$ ist die komplexe Leitfähigkeit, die ohmsche Verluste sowie eine Phasenverschiebung von ${\vec {E^{*}}}$ zu ${\vec {J^{*}}}$ im Material beschreibt. (Die Umformung gilt nur, sofern keine eingeprägte elektrische Feldstärke im Material vorliegt, welche z.B. durch chemische Prozesse hervorgerufen wird.)

wobei ${\vec {H^{*}}},{\vec {J^{*}}},{\vec {D^{*}}}$ komplexe Vektorfelder sind. Anwendung der Rotation und weiterer Maxwellgleichungen (Gaussches Gesetz für Magnetfelder, Induktionsgesetz) ergibt:

$\operatorname {rot} \ \operatorname {rot} \ {\vec {H^{*}}}=\operatorname {grad} \left(\operatorname {div} \,{\vec {H^{*}}}\right)-\Delta {\vec {H^{*}}}=-\Delta {\vec {H^{*}}}=j\omega \left(\varepsilon ^{*}-{\frac {\kappa ^{*}}{\omega }}j\right)\operatorname {rot} \ {\vec {E^{*}}}=j\omega \left(\varepsilon ^{*}-{\frac {\kappa ^{*}}{\omega }}j\right)\left(-j\omega {\vec {B^{*}}}\right)=\omega ^{2}\mu ^{*}\left(\varepsilon ^{*}-{\frac {\kappa ^{*}}{\omega }}j\right){\vec {H^{*}}}={\vec {k^{*}}}^{2}{\vec {H^{*}}}$ ,

wobei die komplexe Permitivitätskonstante $\mu ^{*}$ magnetische Relaxationsprozesse bzw. Verluste durch periodische magnetische Umpolarisierung beschreibt (in der Regel erst im Terahertz-Bereich relevant) und ${\vec {k^{*}}}$ der komplexe Wellenzahlvektor einer entsprechenden TEM-Welle ist. Es ergibt sich also offensichtlich die Helmholzgleichung für die magnetische Feldstärke zu:

$\Delta {\vec {H^{*}}}+{\vec {k^{*}}}^{2}{\vec {H^{*}}}=0$ .

Literatur

Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. 16. Auflage. Springer Verlag, 2005, ISBN 3-540-20792-9.

Basierend auf einem Artikel in:

Wikipedia.de