Lambertsches Gesetz

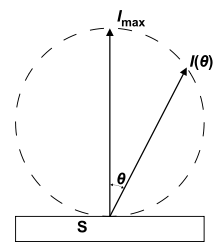
Winkelabhängigkeit der Strahlstärke bei einem Lambert-Strahler.
$\theta$ : Winkel zur Oberflächennormale;
I: Strahlstärke;
S: Quelle oder Reflexionsfläche

Das Lambertsche Gesetz (auch Lambertsches Kosinusgesetz) beschreibt, formuliert von Johann Heinrich Lambert, wie durch den perspektivischen Effekt die Strahlungsstärke mit flacher werdendem Abstrahlwinkel abnimmt. Wenn eine Fläche dem Lambertschen Gesetz folgt und die Strahldichte der Fläche konstant ist, so ergibt sich eine kreisförmige Verteilung der Strahlstärke.

Da der Mensch mit seinem Auge nur die Leuchtdichte bewertet (die Leuchtdichte ist die photometrische Entsprechung der Strahldichte), erscheint ein solches lambertsches Material unabhängig von der Betrachtungsrichtung als gleich hell. Gilt das Lambertsche Gesetz für jedes Oberflächenelement einer Lichtquelle, so bezeichnet man es als Lambert-Strahler. Insbesondere ein idealer schwarzer Körper ist ein Lambert-Strahler. Wird Licht von einer Fläche gemäß dem Lambertschen Gesetz reflektiert, dann spricht man von idealer diffuser Reflexion.

Mathematische Beschreibung

Sei $\theta$ der Winkel gegen die Flächennormale und A die Größe des lambertschen Flächenelements, dann ist die Strahlungsstärke $I(\theta )$ proportional zum Produkt aus Kosinus des Winkels und der Fläche:

$I(\theta )\sim A\cos(\theta )$

Das Verhältnis von Strahlungsstärke und reduzierter Fläche (in Betrachtungsrichtung projiziert), der Proportionalitätsfaktor, ist hierbei die konstante Strahldichte L der Fläche:

$\frac{I(\theta)}{A \cos(\theta)} = L$

Die gestrichelte Linie der Strahlungsstärke im Bild rechts genügt dabei der Gleichung $x^2 + y^2 = y I_\mathrm{max}$ (x-Achse horizontal, y-Achse vertikal).

Experiment

Reflexionsverhalten von Papier. Erläuterung im Text

Die Bilder oben veranschaulichen die Aussage des Lambertschen Gesetzes an einem Experiment. Von links fällt jeweils in Höhe der roten Markierung am Bildrand ein Laserstrahl ein (im rechten Bild rot eingezeichnet) und trifft auf einen senkrecht zur Bildebene stehenden Papierstreifen (weiß eingezeichnet). Der Strahl verläuft flach über einem Schirm, der das vom Papier gestreute Licht (gelbe Pfeile) für die Kamera sichtbar macht. Im ersten Bild steht das Papier senkrecht zum Strahl – die Verteilung des Streulichts ist symmetrisch. Im zweiten Bild steht das Papier schräg – die Verteilung ist nahezu symmetrisch zum Lot auf das Papier, eine leichte Bevorzugung der Streuung in Reflexionsrichtung ist zu erkennen. Im dritten Bild handelt es sich um Transparentpapier, das fast so viel Licht durchlässt wie rückstreut – es liegt keine ausgeprägte Vielfachstreuung mehr vor, sodass die Abweichung vom Lambertschen Gesetz größer ist.

Beispiele

Es gibt in der Realität kein Material, das das Lambertsche Gesetz exakt erfüllt. Insbesondere hat die Strahldichte jeder Oberfläche eine Richtungsabhängigkeit und diese verändert sich, wenn sich die Richtung ändert, aus der die Oberfläche beleuchtet wird. Selbst Normale, die zur Kalibrierung von Messgeräten eingesetzt werden, lassen sich nur in bestimmten Reflexionsrichtungen und Wellenlängenbereichen gut durch das Lambertsche Gesetz beschreiben. Bei Wellenlängen außerhalb des sichtbaren Spektralbereichs und bei Reflexions- bzw. Beleuchtungsrichtungen von mehr als einigen 10° zur Senkrechten, können selbst bei Normalen Abweichungen von mehreren 100 % zum Lambertschen Gesetz auftreten.

Es gibt eine Reihe von Materialien, die einem Lambert-Material zumindest soweit nahekommen, dass sie für das menschliche Auge unter allen Beobachtungsrichtungen annähernd gleich hell erscheinen:

Mattes Papier: Kleine Lufteinschlüsse zwischen den Papierfasern bilden Streuzentren für das sichtbare Licht. Fehlen sie, zum Beispiel nach Tränken des Papiers mit Wasser oder Öl, verliert Papier einen Teil seiner Reflexionseigenschaften und wird transluzent (teilweise lichtdurchlässig).
Diffusor/Milchglas: Auch hier sorgen Streuzentren im Innern eines transparenten Materials dafür, dass Licht diffus gestreut wird. Während Milchglas dabei eher zurückstreut, als dass es durchlässt, werden Diffusoren auch transmissiv eingesetzt.
Die Emissionsfläche von Leuchtdioden (ohne Optik z.B. Linse)
Flächen aus gesintertem PTFE (Spectralon): Optisches PTFE wird oft in einer Ulbricht-Kugel verwendet, die wiederum einen Lambert-Strahler nachbilden soll.
Reflexionsnormale aus gepresstem oder gespachteltem Bariumsulfat

Lommel-Seeliger-Gesetz

Eine bessere Näherung für die Rückstreuung sehr dunkler Flächen ist das Lommel-Seeliger-Gesetz. Es berücksichtigt zusätzlich eine Abhängigkeit vom Beobachtungswinkel $\phi$ :

$I(\theta )={\frac {A\cos(\theta )}{\cos(\theta )+\cos(\phi )}}$

Basierend auf einem Artikel in:

Wikipedia.de