
Winddreieck
Das Winddreieck ist ein navigatorisches Darstellungsverfahren in der Luftfahrt, mit dem sich die Einwirkung von Wind auf Kursrichtung und Geschwindigkeit eines Fahrzeugs grafisch bestimmen lässt. In der Schifffahrt wird analog der Einfluss von Strömungen auf den Kurs bestimmt.
Verwendete Instrumente und Hilfsmittel
Traditionell wird das Winddreieck grafisch aufgestellt. Die bekannten Vektoren werden proportional in eine Zeichnung übertragen. Die unbekannten Größen können dann der Grafik entnommen werden. Als Hilfsmittel, um das aufwändige Zeichnen zu vermeiden, werden auch mechanische Navigationsrechner wie der Aristo-Aviat-Rechner oder der Slide-Graphic-Computer von Jeppesen verwendet. In Flugzeugen und auf Schiffen mit einer erweiterten Navigationsausrüstung werden die Berechnungen durch den Bordcomputer durchgeführt. Dieser nutzt hierfür unter anderem Daten des Trägheitsnavigationssystems, von Bodenfunkstellen und Satelliten.
Voraussetzungen für die Erstellung eines Winddreiecks
Insgesamt sechs Werte bestimmen die Form und Lage des Winddreiecks. Dieses lässt sich sowohl rechnerisch als auch zeichnerisch lösen, wenn jeweils vier der sechs Werte bekannt sind. Der Luvwinkel ergibt sich aus der Differenz zwischen rechtweisendem Steuerkurs (true heading, TH) und rechtweisendem Kurs (true course, TC).
| Richtungen und Winkel | Geschwindigkeiten |
|---|---|
| rechtweisender Steuerkurs rwSK, TH | Fahrt TAS |
| rechtweisender Kurs rwK, TC | Geschwindigkeit über Grund VG, GS |
| Windrichtung TWD | Windgeschwindigkeit VW, WS |
| Luvwinkel (Wind correction angle) WCA |
Grafisches Verfahren
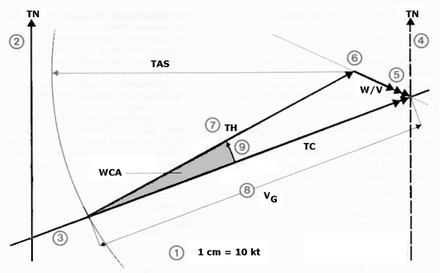
Die Seiten eines Winddreiecks sind Vektoren. Vektoren sind gerichtete Größen. Sie enthalten somit zwei Informationen. Die Pfeilspitze beschreibt die Richtung und die Länge des Pfeils definiert maßstäblich die Geschwindigkeit. Die Seiten des Winddreiecks haben folgende Bezeichnung:
- Steuerkursvektor
- Richtungsinformation: rwSK oder TH (true heading): Richtung, in die die Flugzeuglängsachse zeigt.
- Geschwindigkeitsinformation: VE oder TAS (true airspeed): Geschwindigkeit des Flugzeugs gegenüber der umgebenden Luft.
- Symbol: −−−>
- Kurs-über-Grund-Vektor
- Richtungsinformation: rwK oder TC (true course): Kurs, den das Flugzeug über Grund zurücklegt.
- Geschwindigkeitsinformation: VG oder GS (ground speed): Geschwindigkeit über Grund.
- Symbol: −−−>>
- Wind-Vektor W/V (wind vector)
- Windrichtung WR oder TWD (true wind direction)
- Windgeschwindigkeit: VW oder WS (wind speed)
- Symbol: −−−>>>
Konstruktion des Winddreiecks
- Maßstab für die Geschwindigkeit festlegen
(beispielsweise 10 kn = 1 cm, um die Konstruktion auf einem DIN-A4-Blatt zeichnen zu können) - TN festlegen (true north – rechtweisend Nord) oder geografisch Nord; wahre geografische Nordrichtung – stimmt mit N auf der Karte überein
- TC einzeichnen (true course – rechtweisender Kartenkurs) auch rechtweisender Kurs (rwK) genannt: der Kurs, den das Flugzeug tatsächlich zurücklegt, der also auf der Karte eingezeichnet ist.
- Hilfsmeridian in Kursrichtung einzeichnen
- Wind-Vektor (Wind mit ursprünglicher Richtung) im Schnittpunkt Hilfsmeridian / TC mit Windgeschwindigkeit eintragen
- Um den Anfangspunkt des Windvektors Kreisbogen mit TAS (true airspeed – wahre Eigengeschwindigkeit) auf TC schlagen
- Schnittpunkt Kreisbogen / TC mit Anfangspunkt des Wind-Vektors verbinden (Steuerkurs-Vektor)
- Auf TC (Kurs-über-Grund-Vektor) Grundgeschwindigkeit (VG) ausmessen, Maßstab berücksichtigen
- WCA (wind correction angle – Windvorhaltewinkel) zwischen TC und TH messen
Rechnerisches Verfahren
Rechnerisch lassen sich die einzelnen Werte mit Hilfe des Sinussatzes bestimmen:
- WA = wind angle (dt. Windwinkel) = Winkel zwischen dem Kurs-über-Grund-Vektor und dem Windvektor
- WS, WCA, TAS, GS siehe oben unter Grafisches Verfahren.
Die dazugehörige Crosswindkomponente (Seitenwind) ergibt sich aus:
Die dazugehörige Head-/Tailwindkomponente (Gegen-/Rückenwind) ergibt sich aus:
Der dazugehörige Luvwinkel (zum Steuerkurs) ergibt sich aus:
Zur Berechnung des Windwinkels (WA) gilt: Ist die Differenz
> 180°, so zieht man von der Differenz 360° ab. Ist die Differenz < −180°,
so addiert man 360° hinzu. Ansonsten ist der Windwinkel die Differenz.
Literatur
- Jeppesen Sanderson: Privat Pilot Manual. 2001, ISBN 0-88487-238-6
- Walter Air: CVFR Lehrbuch, Mariensiel, 2001
- FSM, Flugsicherheitsmitteilungen 2/86, Flugbetrieb-Kurs. Luftfahrt-Bundesamt (D), Braunschweig, 16. Dezember 1986
- Wolfgang Kühr: Der Privatflugzeugführer, Flugnavigation. Verlag Friedrich Schiffmann, Bergisch Gladbach 1979, ISBN 3-921270-05-7


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.12. 2022