Sichtweite

Als Sichtweite oder Sicht im engeren Sinne bezeichnet man die größte horizontale Entfernung, bei der im Gelände ein dunkles Objekt in Bodennähe gerade noch vor hellem Hintergrund erkannt werden kann. Sie wird auch als meteorologische Sichtweite bezeichnet, im Unterschied zu anderen Sichtweiten:

Sichtweite bei Nacht ( Nachtsicht, Feuersicht), bei der eine Lichtquelle von einem Beobachter gerade noch wahrgenommen wird, ebenfalls meteorologisch begrenzt.
Die geometrische oder geografische Sichtweite ist von der Erdkrümmung begrenzt und wird von den Höhenposition des Betrachters und des Ziels sowie geografischen Sichthindernissen beeinflusst.
- Unter Berücksichtigung der atmosphärischen Refraktion ergibt sich daraus die geodätische Sichtweite.

Atmosphärische Sichtweite

Links: Sicht bei klarem Wetter; Rechts: Nebelreduzierte Sichtweite

Abnahme des Kontrastes relativ zum Himmel mit zunehmender Entfernung der Berge

Drei Effekte schränken die Atmosphärische Sichtweite ein:

atmosphärisch: Hydrometeore wie Niederschläge, Schneefall oder Nebel oder Lithometeore wie Staub oder Rauch dämpfen das Licht beziehungsweise den Kontrast
Luftverschmutzung: Aerosole verursachen eine zusätzliche Lichtdämpfung

Atmosphärische Streuung und Absorption reduzieren den Kontrast eines Objekts relativ zur Umgebung. Dieses Phänomen nennt man Lichtdämpfung. Der Kontrast hängt exponentiell von der Entfernung und einem Absorptionskoeffizienten $\sigma$ ab:

$K=K_{0}\cdot e^{-\sigma \cdot s}$

Für die Wahrnehmung ist ein Mindestkontrast von

$K=0{,}02\;{\hat {=}}\;2\%$

erforderlich. Unter der Annahme, dass der Ausgangskontrast $K_{0}$ ungefähr 1 ist, kann unmittelbar aus der Sichtweite auf $\sigma$ geschlossen werden:

$\sigma ={\frac {\ln(50)}{\mathrm {s} }}\approx {\frac {3{,}91}{\mathrm {s} }}$

Eine Sichtweite von 50 km entspricht einer Absorptionskonstanten von $10^{-4}/\mathrm {m}$ . Bei guten Bedingungen beträgt die Fernsicht einige hundert Kilometer, siehe Tabelle.

Im Beispielbild nimmt der Kontrast der Berge zum Himmel mit zunehmender Entfernung ab. Die Bergkette im rechten Bild ist bei Nebel nicht mehr zu sehen.

Wetterabhängigkeit der Sichtweite
Wetterbedingung	Sichtweite in km
Außergewöhnlich klar	280
Sehr klar	50
Klar	20
Leicht diesig	10
Diesig	4
Starker Dunst, leichter Nebel	2
Mäßiger Nebel	1
Dichter Nebel, Starkregen	0,1
Extremer Nebel, Schneetreiben	0,01

Sichtweite im Wasser

Reines Meerwasser hat je nach Wellenlänge eine Extinktionslänge 1/σ von 2-100 m. Bei Tauchgängen in Naturgewässern gilt eine Sichtweite von 40 Metern als außerordentlich gut. Die Sicht kann getrübt werden durch Schwebeteilchen (Plankton, Blütenstaub, Wüstensand), durch Schwemmteilchen in Strömungen (Flussmündung) oder durch Abwässer und die Einleitung chemischer Stoffe.

Geodätische Sichtweite

Berechnung

Die Geodätische Krümmung der Erde begrenzt die maximale Sichtweite für Objekte von einem Standpunkt auf der Erdoberfläche bzw. auf sphärisch gekrümmten Körpern. Die Sichtweite von einem erhöhten Beobachtungspunkt oder eines hohen Objekts (z.B. Berggipfel) aus einer Ebene oder von der Meeresoberfläche aus lässt sich nach dem Satz des Pythagoras berechnen, da Sichtverbindung und Erdradius die Katheten eines rechtwinkligen Dreiecks bilden und der Abstand des erhöhten Punktes vom Erdmittelpunkt dessen Hypotenuse:

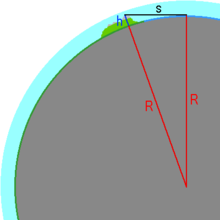
Rechtwinkliges Dreieck zur Berechnung der Sichtweite

(1) $s^{2}+R^{2}=(R+h)^{2}$

(2) $s={\sqrt {(R+h)^{2}-R^{2}}}$

Nach der ersten binomischen Formel ergibt sich daraus:

(3) $s={\sqrt {R^{2}+2Rh+h^{2}-R^{2}}}={\sqrt {2Rh+h^{2}}}$

Da außer in der Raumfahrt $h^{2}$ gegenüber 2Rh vernachlässigbar klein ist, lässt sich die Formel vereinfachen zu

(4) $s\approx {\sqrt {2Rh}}={\sqrt {2R}}\cdot {\sqrt {h}}$

Die folgenden, dem praktischen Gebrauch dienenden (und mit Zusatzbuchstaben nummerierten) Formeln ergeben die Sichtweite s in km, wobei die Höhe h in Metern einzusetzen ist. (Um auf diese praktikablen Maßeinheiten zu kommen, wurde der mittlere Erdradius von R = 6370 km gegenüber (4) bzw. (6) mit 6,37 Megameter berücksichtigt.)

(5a) ${\underline {s\approx 3{,}57\cdot {\sqrt {h}}}}$

Die Refraktion der Atmosphäre krümmt die Lichtstrahlen und lässt die Erde größer erscheinen. Der mittlere scheinbare Erdradius liegt bei R_k ≈ 7680 km. Die optische Sehweite vergrößert sich normalerweise um ungefähr 10 % (in Ausnahmefällen aber auch erheblich mehr oder weniger):

(5b) ${\underline {s_{\mathrm {opt} }\approx 3{,}9\cdot {\sqrt {h}}}}$

Bei der Reichweite von elektromagnetischen Wellen sehr kurzer Wellenlänge (Ultrakurzwelle und kürzer) ist der scheinbare Erdradius für UHF zu verwenden. Er liegt bei R_k ≈ 8470 km:

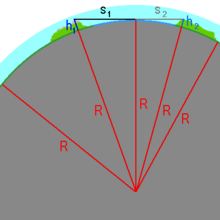
(5c) ${\underline {s_{\mathrm {UHF} }\approx 4{,}1\cdot {\sqrt {h}}}}$

Sichtweite zwischen zwei erhöhten Punkten. Von jedem der beiden Berggipfel gesehen, ragt der jeweils andere nur knapp über den Horizont.

Sind Augen und Objekt über die Referenzebene erhoben, was schon durch die Augeshöhe der in der Ebene stehenden Person gegeben ist, so addieren sich die Abstände beider von der Stelle, wo die sie verbindende Tangente die Erdoberfläche berührt.

(6a) $s=s_{1}+s_{2}\approx {\sqrt {2R}}\cdot \left({\sqrt {h_{1}}}+{\sqrt {h_{2}}}\right)$

beziehungsweise

(6b) ${\underline {s\approx 3{,}9\cdot \left({\sqrt {h_{1}}}+{\sqrt {h_{2}}}\right)}}$

Beispiele

Ein Schiff am Horizont: der Schiffsrumpf ist durch die Erdkrümmung verdeckt.

Im rechten Bild sieht man ein Schiff am Horizont, von dem die Erdkrümmung einen Teil des Rumpfs verdeckt. Die Aufnahme entstand bei einer Blickhöhe von $h_{1}=2$ m. Nimmt man an, dass der verdeckte Teil des Rumpfs eine Höhe von ca. $h_{2}=5$ m über dem Wasserspiegel hat, ist das Schiff ca. 14,2 km entfernt (mit Berücksichtigung der atmosphärischen Refraktion nach der obigen Formel 6b).

Die Tabelle stellt einige Werte für die maximale geometrische Sichtweite zusammen. Daran wird die Bedeutung der Höhe des Ausgucks alter Kriegsschiffe deutlich. Von einem 15 m hohen Mast kann der Beobachter ein Schiff in 15 km Entfernung ausmachen. Umgekehrt sieht die Wache dort von 0 m Höhe aus nur mit viel Glück den kleinen Mast am Horizont.

Geometrische Sichtweiten (h₂ = 0 m; ohne Berücksichtigung der atmosphärischen Refraktion)

Augenhöhe	Sichtweite
01 m	03,6 km
02 m	05,0 km
03 m	06,1 km
04 m	07,1 km
05 m	08,0 km
06 m	08,7 km
07 m	09,4 km
08 m	010,0 km
09 m	010,7 km

Augenhöhe	Sichtweite
010 m	011 km
020 m	016 km
030 m	019 km
040 m	022 km
050 m	025 km
060 m	027 km
070 m	029 km
080 m	031 km
090 m	033 km

Augenhöhe	Sichtweite
0100 m	035 km
0200 m	050 km
0300 m	061 km
0400 m	071 km
0500 m	079 km
0600 m	087 km
0700 m	094 km
0800 m	0100 km
0900 m	0107 km

Augenhöhe	Sichtweite
01000 m	0112 km
02000 m	0159 km
03000 m	0195 km
04000 m	0225 km
05000 m	0252 km
06000 m	0276 km
07000 m	0298 km
08000 m	0319 km
09000 m	0338 km

Geographische Breite

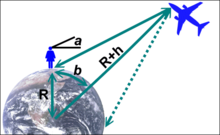
Schemazeichnung zur Bestimmung des Winkel-Sichtbarkeitsbereichs b auf der Erde

Bei hochfliegenden Objekten wie Flugzeugen vor allem aber Satelliten ist man weniger an der Sichtweite als Entfernungsangabe interessiert. Stattdessen möchte man wissen, welcher Bereich der Erde, ausgedrückt in Winkelgraden, der Beobachtung zugänglich ist oder Signale empfangen kann. In der Schemazeichnung sieht ein Beobachter ein Flugzeug im Winkel a über dem Horizont. Es fliegt in der Höhe h über der Erde und der Höhe h+R über dem Erdmittelpunkt. Das Flugzeug ist auf der Erde mit einer Elevation ≥a im Winkelbereich von 2·b zu sehen^[1] (Winkel in Bogen):

(1) $b=b(a)={\frac {\pi }{2}}-\arcsin \left({\frac {R}{R+h}}\cos(a)\right)-a$

Bei einer Elevation von a=0, wenn das Flugzeug gerade am Horizont zu erkennen^[1] ist, vereinfacht sich (1) zu:

(2) $b(0)=\arccos \left({\frac {R}{R+h}}\right)$

Die Beziehung (2) gibt ebenfalls an, um wie viel sich die Kimm aus einer erhöhten Beobachtungsposition heraus verschoben hat.

Als Näherung gilt:

(2b) : $\kappa _{\mathrm {geom} }=1{,}93\cdot {\sqrt {H}}$

bzw.

(2c) : $\kappa _{\mathrm {opt} }=1{,}75\cdot {\sqrt {H}}$

Beispiele:

Aus einer Flughöhe von h = 10 km sieht ein Pilot einen Bereich auf der Erde von 2·b = 3,2°, entsprechend einer Fläche mit einem Durchmesser von ca. 350 km. Den Randbereich erkennt er nur streifend. Bei einem Elevationswinkel von a = 10° reduziert sich der Durchmesser auf ca. 50 km.
Ein Satellit in 36.000 km Höhe erfasst einen Bereich von maximal 2·81,3° .
Messungen, die mit einem Sextanten bei einer Augenhöhe von 4 m über der Wasseroberfläche durchgeführt werden, müssen je nach Zustand der bodennahen Atmosphäre normalerweise um 3,5′ bis 3,8′ korrigiert werden.

Siehe auch

zur Sehweite Akkommodation (Auge)
Entfernungsmessung

Einzelnachweise

↑ ^a ^b "Sehen" und "Erkennen" ist hier rein theoretisch gemeint. Ein Verkehrsflugzeug mit Rumpfdurchmesser von 8 Metern ist ab etwa 40 Kilometer Entfernung mit bloßem Auge nicht mehr vom Himmel zu unterscheiden. Siehe Auflösungsvermögen.

Basierend auf einem Artikel in:

Wikipedia.de