Kinetik (Technische Mechanik)

Stellung der Kinetik in der Technischen Mechanik

Die Kinetik (griechisch kinesis ‚Bewegung‘) ist ein Teilgebiet der Technischen Mechanik und beschreibt die Änderung der Bewegungsgrößen (Ort, Geschwindigkeit und Beschleunigung) unter Einwirkung von Kräften im Raum und berücksichtigt dabei meist auch die Masse der bewegten Körper. Die Kinematik dagegen beschreibt die Bewegung eines Körpers (Ort, Geschwindigkeit, Beschleunigung) ohne dabei Kräfte oder Massen zu berücksichtigen.

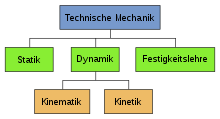
Die Technische Mechanik wird meist eingeteilt in die drei Gebiete Statik, Festigkeitslehre und Dynamik die dann aus den beiden Teilgebieten der Kinetik und der Kinematik besteht. In der Physik wird dagegen die Mechanik in die Kinematik und die Dynamik eingeteilt welche dort die Statik und die Kinetik enthält.

Wichtige Sätze der Kinetik

Über die Sätze der Kinetik lässt sich die Bewegungsgleichung eines Systems in Abhängigkeit von den frei wählbaren verallgemeinerten Koordinaten aufstellen.

Schwerpunktsatz oder Impulssatz

Zu den bekanntesten Sätzen der Dynamik gehört das sogenannte Grundgesetz der Dynamik das zweite Newtonsche Gesetz (auch Impulssatz genannt)

${\vec F}=m\cdot {\vec a}_{{\mathrm {s}}}$ .

Dabei ist ${\vec F}$ die Kraft, m die Masse und ${\vec a}_{{\mathrm {s}}}$ die Beschleunigung.

Diese Gleichung gilt nur für eine zeitlich konstante Masse m. Für den allgemeinen Fall einer zeitlich veränderlichen Masse muss die Kraft als die Ableitung des Impulses ${\vec {p}}=m{\vec {v}}$ nach der Zeit definiert werden:

${\vec F}={\frac {{\mathrm {d}}{\vec {p}}}{{\mathrm {d}}t}}={\frac {{\mathrm {d}}}{{\mathrm {d}}t}}(m{\vec {v}})=m{\frac {{\mathrm {d}}{\vec {v}}}{{\mathrm {d}}t}}+{\frac {{\mathrm {d}}m}{{\mathrm {d}}t}}{\vec v}$ .

Dabei ist ${\vec {v}}$ die Geschwindigkeit.

Leistungssatz

Mit dem Leistungssatz der Mechanik lassen sich auch nicht-konservative Systeme mit einem Freiheitsgrad beschreiben.

Energiesatz

Der Energiesatz der Mechanik folgt als Spezialfall aus dem Leistungssatz für konservative Systeme.

Arbeitssatz

Der Arbeitssatz

$W=\int F{\mathrm {d}}s$

bildet schließlich die vierte Möglichkeit, die Bewegungsgleichung eines dynamischen Systems zu ermitteln.

Basierend auf einem Artikel in:

Wikipedia.de