g-Kraft

Beispiel: Verdreifachung der g-Kraft in einem Flugzeug durch Flug in einer aufwärts gekrümmten Bahn

g-Kräfte werden Belastungen genannt, die aufgrund starker Änderung von Größe und/oder Richtung der Geschwindigkeit auf den menschlichen Körper, einen Gebrauchsgegenstand oder ein Fahrzeug einwirken. Bei Belastungen technischer Geräte wie Flugzeugen oder der Angabe von Belastungsgrenzen wird auch der Begriff Lastvielfache verwendet. Es handelt sich bei der g-Kraft um eine „Kraft pro Masse“, sie hat daher die Dimension einer Beschleunigung und wird als Vielfaches der Fallbeschleunigung g angegeben. Hohe g-Kräfte treten beispielsweise bei Fahrten mit einer Achterbahn, bei Raketenstarts oder bei Zusammenstößen von Gegenständen auf.

Physikalische Grundlagen

Ein Rennfahrer spürt beim Start eine Kraft, die ihn – entgegen der Beschleunigungsrichtung – nach hinten in seinen Sitz presst. Diese Kraft kommt dadurch zustande, dass der Rennwagen nach vorne beschleunigt wird. Der Körper des Fahrers würde wegen seiner Trägheit gegenüber dieser Beschleunigung zurückbleiben, wenn er nicht durch den Sitz mitgerissen würde. Was der Fahrer also fühlt, ist keine tatsächliche äußere Kraft, die ihn stärker nach hinten in den Sitz drückt, sondern seine eigene Trägheit, die sich hier in Form einer Trägheitskraft bemerkbar macht. Der Fahrer wird vom Sitz nach vorne beschleunigt.

Nach der Grundgleichung der Mechanik erfährt der Körper des Fahrers (Masse ) die Beschleunigung a=F/m , wenn auf ihn eine Kraft wirkt. Dabei kann der physikalische Begriff Beschleunigung je nach Richtung der Kraft umgangssprachlich auch Abbremsung oder Richtungsänderung bedeuten. Der Fahrer ist relativ zu seinem Fahrzeug in Ruhe. In der Physik spricht man von einem beschleunigten Bezugssystem. Für ihn herrscht ein Kräftegleichgewicht zwischen der beschleunigenden Kraft und der Trägheitskraft F^* . Die Trägheitskraft ist also entgegengesetzt gleich groß wie die äußere Kraft. Daher eignet sich die Beschleunigung dazu, die auf die Masse bezogene Trägheitskraft zu quantifizieren. Hierbei wird dann die Beschleunigung oft als Vielfaches der Erdbeschleunigung $g\approx 9{,}81\;{\mathrm {m/s^{2}}}$ angegeben, weil dies mit der Alltagserfahrung leicht zu vergleichen ist: „“ bedeutet also, dass die erfahrene Beschleunigung gleich groß wie die Erdbeschleunigung ist und dass folglich die Trägheitskraft gleich groß wie die Gewichtskraft (auf der Erde) ist.

Spezialfälle

Gleichmäßige geradlinige Beschleunigung

Wenn ein Körper auf der Strecke von der Ruhe gleichmäßig auf die Geschwindigkeit beschleunigt wird, dann beträgt seine Beschleunigung:

$a={\frac {v^{2}}{2s}}$

Dies folgt durch Umstellung aus den Weg-Zeit- und Geschwindigkeits-Zeit-Gesetzen der gleichmäßig beschleunigten Bewegung:

$s={\frac 12}at^{2}$ bzw. v=at

Dieselbe Formel ergibt sich für den Betrag der Beschleunigung bei einem Körper, der auf der Strecke von der Geschwindigkeit bis auf Null abbremst.

Beispiele

Ein Auto fährt mit 30 km/h gegen eine feste Wand, dabei wird die Knautschzone um 50 cm gestaucht. Die g-Kraft beträgt 7g. Bei 50 km/h und gleichem Verformungsweg beträgt die Beschleunigung fast 20g.

Ein Körper fällt aus 1 m Höhe auf den Boden. Je starrer Körper und Boden sind, desto höher ist die g-Kraft. Gibt der Boden nicht nach und der Körper verformt sich um 0,1 mm und bleibt dann liegen, dann wurde er mit im Mittel 10.000g abgebremst.

Kurvenfahrt

Wenn ein Körper mit der Geschwindigkeit eine Kurve durchläuft, die den Radius hat, dann erfährt er die Beschleunigung

$a={\frac {v^{2}}{r}}.$

Beispiel

Ein Rennwagen durchfährt mit einer Geschwindigkeit von 200 km/h eine Kurve mit einem Radius von 160 m, dann beträgt die Zentripetalbeschleunigung ca. $19{,}3\;{\mathrm {m/s^{2}}},$ was etwa entspricht.

Beispiele von g-Werten in Natur, Technik und Alltag

Maschine oder Ereignis	g-Faktor
Typischer Maximalwert bei einer Kinderschaukel ^[1]	1.0002,5
Maximalwert bei der Achterbahn Silver Star	1.0004
Maximalwert bei einer Apollo-Kapsel während des Wiedereintritts in die Erdatmosphäre nach einem Mondflug	1.0007,19
Durchschnittliche Maximalwerte bei Kunstflugmanövern (Belastungsdauer zwischen 1,5 und 3 Sekunden)	1.0008
Maximalwert für von Menschen ohne schwere Verletzungen überlebbare g-Kraft bei günstiger Wirkrichtung der Beschleunigung und kurzer Beschleunigungsdauer (Sekundenbruchteile)	1.0100
Laut Guinness-Buch der Rekorde höchste gemessene g-Kraft, die von einem Menschen (David Purley, 1977) überlebt wurde	1.0180
IndyCar von Kenny Bräck beim Crash auf dem Texas Motor Speedway im Jahre 2003 (der Fahrer überlebte)	1.0214
Größenordnung beim Aufprall eines Kugelschreibers, der aus 1 m Höhe auf harten Boden fällt und liegen bleibt ^[2]	01.000

Auswirkungen von g-Kräften auf den menschlichen Körper

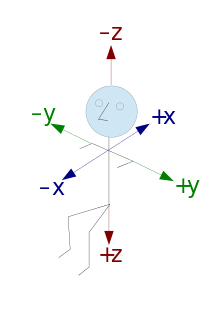
Koordinatensystem zur Bestimmung der Richtung der g-Kraft

Einflussfaktoren

Die Auswirkung von g-Kräften auf den menschlichen Körper hängen stark von der Richtung der Einwirkung ab. Üblicherweise wird ein Koordinatensystem wie im Bild rechts verwendet. Positive g-Kräfte in z-Richtung erfährt ein Organismus beispielsweise, wenn er bei einem Innenlooping auf einer Achterbahn in den Sitz gedrückt wird; negative, wenn er bei einem Außenlooping aus dem Sitz herausgehoben wird.

Außer der Stärke und der Richtung der Kräfte ist auch von großer Bedeutung, wie lange sie wirken. Kurzzeitig kann der menschliche Körper relativ hohen Belastungen standhalten (wobei mit „kurzen“ Zeiträumen Sekundenbruchteile gemeint sind). Bei länger anhaltenden Kräften besteht bereits ab einer vergleichsweise geringen Stärke die Gefahr von Durchblutungsstörungen.

Richtungsabhängigkeit der Symptome

Bei positiven g-Kräften in z-Richtung (ausgeübt durch den Sitz und Boden, den sitzenden Menschen nach oben beschleunigend) besteht die Gefahr, dass das Blut in die Beine versackt. Dadurch kann es zu Sehstörungen bis hin zur Bewusstlosigkeit infolge eingeschränkter Hirndurchblutung kommen (Bewusstseinsstörungen). Dieses Phänomen wird auch als g-LOC (“Loss Of Consciousness”) bezeichnet. Der Bewusstlosigkeit voraus geht der sogenannte Greyout und später Blackout, der durch die ungenügende Blutversorgung der Netzhaut (Retina) des Auges zustande kommt. Um die in Kampfflugzeugen auftretende Belastung besser ertragen zu können, werden deren Besatzungen Anti-g-Anzüge angepasst, die die Effekte der g-Kräfte beschränken sollen, indem der Anzug bei hohen Beschleunigungen die Beine komprimiert. Sobald die Beschleunigungskräfte nicht mehr einwirken, ist die Hirn- und Augendurchblutung wieder normal, und die Bewusstlosigkeit endet. In der nachstehenden Tabelle sind die Reaktionen des untrainierten menschlichen Körpers auf verschiedene (mehrere Minuten andauernde) positive g-Kräfte in z-Richtung aufgeführt.

Belastung	Symptome
1–2 g	uneingeschränkt ertragbar
2–3 g	beginnende Einengung des Gesichtsfeldes
3–4 g	röhrenförmiges Gesichtsfeld, Greyout
4–5 g	Blackout
5–6 g	Bewusstlosigkeit

Negative g-Kräfte in z-Richtung (Gurtzeug zieht den Menschen nach unten) bewirken einen Blutfluss zum Kopf hin. Sie können vom Menschen erheblich schlechter ertragen werden. Bereits zwei bis drei g können zum Redout führen.

In x-Richtung (Beschleunigung des sitzenden Menschen nach vorne durch Druckkraft der Sessellehne) werden g-Kräfte von Menschen besser ertragen, führen aber ab einer Stärke von 20g zu Atemproblemen. In y-Richtung - quer zum Körper - ist dagegen häufig, wenn der Kopf seitlich nicht gestützt wird, die Überlastung der Nackenmuskulatur das Hauptproblem.

Historische Entwicklung

Die Auswirkungen hoher g-Werte wurden erstmals ausführlich 1946–1948 durch den US-amerikanischen Mediziner John Paul Stapp im Dienst der US-Armee untersucht. Im Rahmen des Projekts wurden dabei auch er selbst und andere Freiwillige auf schienengeführten Schlitten mittels Raketenantrieben auf hohe Geschwindigkeiten beschleunigt und mit speziellen Bremsvorrichtungen abgebremst. Die Ergebnisse dieser Forschungen trugen viel zur Entwicklung von effektiven Rückhalte- und Rettungssystemen bei.

g-Kräfte in der Luftfahrt

Berechnung des Lastvielfachen bei einem Kurvenflug in Abhängigkeit vom Querneigungswinkel θ

g-Faktor (n) im Kurvenflug als Funktion der Querneigung $\beta$

Bei g-Kräften, die auf Flugzeuge im Flug wirken, wird zwischen Manöverlasten und Böenlasten unterschieden. Unter Böenlasten versteht man g-Kräfte, die durch Böen, also durch Luftbewegungen, die eine kurzzeitige Änderung der Anströmung hervorrufen, entstehen. Manöverlasten entstehen durch Flugmanöver. Um Belastungsgrenzen von Flugzeugen zu definieren, wird die Bezeichnung „Lastvielfache“ verwendet. Das Lastvielfache ist als dimensionslose Zahl definiert durch das Verhältnis von Auftriebskraft $F_\mathrm{A}$ zu Gewichtskraft :

$n={\frac {F_{{\mathrm {A}}}}{G}}$

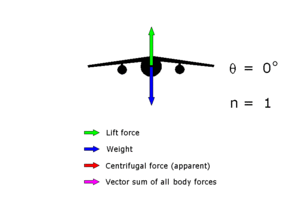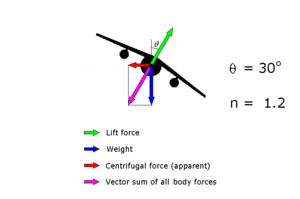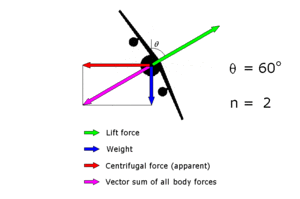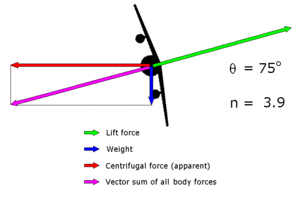
Wenn man davon ausgeht, dass keine zusätzlichen Kräfte wirken, etwa durch Änderung der Triebwerksleistung oder Geschwindigkeitsänderung der Umgebungsluft, dann entspricht das Lastvielfache n der g-Kraft, die auf die Menschen an Bord des Flugzeugs wirkt. Das Lastvielfache ist der Faktor, um den die scheinbare Gewichtskraft auf Gegenstände im Flugzeug durch zusätzliche Trägheitskräfte zunimmt. Um die entsprechende g-Kraft zu erhalten, muss das Lastvielfache n daher mit der Fallbeschleunigung g multipliziert werden. 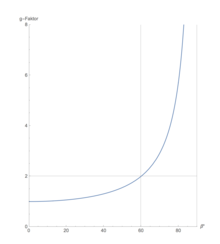Für einen normalen Reiseflug ergibt sich ein Lastvielfaches von n=1 , entsprechend einer g-Kraft von 1g. Im Kurvenflug ist das Lastvielfach $n=1/\cos(\beta )$ , wobei $\beta$ die Querneigung ist.

Die Angabe von maximalen Lastvielfachen wird benutzt, um die Strukturfestigkeit eines Flugzeugs und damit zulässige Flugmanöver festzulegen. Beispiel: Eine Beechcraft Bonanza A36 darf bei eingefahrenen Landeklappen und bei Höchstabfluggewicht mit einem g-Faktor von höchstens 4.4 belastet werden. Dieses Lastvielfach wird bei einer Querneigung von 77° erreicht.

Stoßresistenz

Die Widerstandsfähigkeit eines Gebrauchsgegenstands gegenüber kurz andauernden g-Kräften durch Stöße und Vibrationen (Erschütterungen) wird als Stoßresistenz bezeichnet. Angaben über Stoßresistenz findet man zum Beispiel häufig in Datenblättern von Festplatten. Die g-Kräfte werden meist nur sehr kurz ausgehalten (Größenordnung 1 ms), angegebene Grenzwerte gelten oft nur bei einer bestimmten Form der Belastung.

Anmerkungen

↑ Die Zentrifugalbeschleunigung, die zusätzlich zur Erdbeschleunigung wirkt, lässt sich für einen anfänglichen Auslenkungswinkel $\phi$ durch $2g\,(1-\cos \phi )$ berechnen.
↑ Durchschnittliche Verzögerung, wenn der Boden oder Kugelschreiber beim Aufprall um 1 mm nachgibt. Der Wert lässt sich durch Erdbeschleunigung·Höhe/Verzögerungsstrecke berechnen.

Basierend auf einem Artikel in:

Wikipedia.de