
Inkommensurabilität (Mathematik)
In der Mathematik heißen zwei reelle
Zahlen
und
kommensurabel (von lateinisch
commensurabilis ‚gleich zu bemessen,
gleichmäßig‘),
wenn sie ganzzahlige
Vielfache einer geeigneten
dritten reellen Zahl
sind, also einen gemeinsamen Teiler
besitzen. Die Bezeichnung kommt daher, dass man sie dann mit dem gemeinsamen Maß
messen kann. In mathematischer
Notation:
, sodass
mit
.
Daraus folgt, dass das Verhältnis
von
und
eine rationale
Zahl ist:
.
Gibt es kein auch noch so kleines gemeinsames Maß ,
dann heißen die Zahlenwerte
und
inkommensurabel (von lateinisch
incommensurabilis ‚unmessbar‘),
d.h. ihr Verhältnis ist eine irrationale
Zahl.
Der Ausdruck Inkommensurabilität, der auf Euklids Elemente zurückgeht, bezieht sich direkt auf das geometrische Messen von Strecken mit tatsächlichen Messlatten. Er stellt eine gute Erinnerung daran dar, dass die griechische Mathematik unmittelbar auf der anschaulichen Geometrie beruhte, deren „Anschaulichkeit“ eben durch die Inkommensurabilität überschritten wurde.
Beispiele
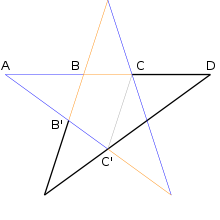
- Alle natürlichen Zahlen sind kommensurabel, denn sie haben das Vergleichsmaß c = 1.
- Endlich viele beliebige Brüche sind kommensurabel, denn man kann
sie auf einen Hauptnenner
bringen, und ein Vergleichsmaß ist dann
.
- Inkommensurabel zu den Bruchzahlen sind dagegen alle Zahlen, die sich nicht als Brüche schreiben lassen.
- Die Seite a eines Quadrats und die Länge d seiner Diagonalen
sind inkommensurabel, denn nach dem Satz des
Pythagoras ist
, und die Annahme, dass dies eine Bruchzahl ist, lässt sich widerlegen.
- Inkommensurable Strecken gibt es auch beim Fünfstern oder Pentagramm, nämlich die innere Strecke (BC) und die äußere Strecke (AD).
Geschichte
Der erste Beweis für die Existenz von inkommensurablen Strecken wird seit der Antike dem Pythagoreer Hippasos von Metapont zugeschrieben, der im späten 6. und frühen 5. Jahrhundert v. Chr. lebte. Diese Überlieferung entspricht möglicherweise den Tatsachen. Eine Erfindung ist jedoch die daran anknüpfende Legende, der zufolge die Pythagoreer die Inkommensurabilität als Geheimnis behandelten; Hippasos soll dieses Geheimnis verraten haben, was angeblich seinen Tod zur Folge hatte. Diese Erzählung ist aus einem Missverständnis entstanden. In Zusammenhang mit der Legende vom Geheimnisverrat wurde in älterer Forschungsliteratur die Hypothese vertreten, die Entdeckung der Inkommensurabilität habe die Pythagoreer schockiert und habe eine Grundlagenkrise der Mathematik bzw. der Philosophie der Mathematik ausgelöst. Die Annahme einer Grundlagenkrise wird jedoch ebenso wie der angebliche Geheimnisverrat von der neueren Forschung einhellig abgelehnt. Die Entdeckung der Inkommensurabilität wurde als Errungenschaft und nicht als Problem oder Krise betrachtet.
Siehe auch
- Teilerfremdheit bei natürlichen Zahlen
- Goldener Schnitt
Literatur
- H. Vogt: Die Entdeckungsgeschichte des Irrationalen nach Plato und anderen Quellen des 4. Jahrhunderts, Bibliotheca Math. (3) 10, 97–155 (1910).
- E. Frank: Platon und die sogenannten Pythagoreer, Niemeyer, Halle, 1923.
- B. L. van der Waerden: Zenon und die Grundlagenkrise der griechischen Mathematik. Math. Ann. 117, (1940). 141–161.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.02. 2022