Zufallsgraph

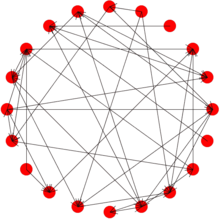
Realisierung des Gilbert-Graphen $G(20;\;0{,}1)$

Ein Zufallsgraph bezeichnet einen Graphen, bei dem die Kanten zufällig erzeugt werden. Häufig eingesetzte Modelle zufälliger Graphen sind:

Das Gilbert-Modell (benannt nach Edgar Gilbert):^[1] $G(n,p)$ mit einer natürlichen Zahl $n\geq 1$ , der Zahl der Knoten, und einer Wahrscheinlichkeit $0\leq p\leq 1$ bezeichnet die Menge aller Graphen, bei denen für jedes geordnete Paar $(v_{1},v_{2})$ von Knoten, mit $v_{i}\leq n$ , mit der Wahrscheinlichkeit $p$ bestimmt wird, ob sie durch eine Kante verbunden werden, und das unabhängig von den anderen Kanten. Man untersucht dann häufig, mit welcher Wahrscheinlichkeit die erzeugten Graphen eine bestimmte Eigenschaft haben, z.B. ob sie zusammenhängend sind. Eine weitere Möglichkeit ist es, $p=p(n)$ in Abhängigkeit von $n$ vorzugeben und dann das Verhalten bei wachsendem $n$ zu untersuchen.

Das Erdős-Rényi-Modell (benannt nach Paul Erdős und Alfréd Rényi):^[2] $G(n,m)$ mit natürlichen Zahlen $n\geq 1$ und $m\geq 0$ bezeichnet die Menge aller Graphen mit exakt $n$ Knoten und $m$ Kanten.

Die Knoten $V$ des Graphen $G$ werden in der Ebene gemäß einer vorgegebenen Wahrscheinlichkeitsverteilung $f$ verteilt. Wenn zwei Knoten $v_{1},v_{2}$ einen Abstand kleiner als eine vorgegebene Grenze $d$ haben, werden sie durch eine Kante verbunden.

Auf einer abzählbaren Knotenmenge kann jede Kante unabhängig und mit Wahrscheinlichkeit ${\tfrac {1}{2}}$ gewählt werden – durch diese Konstruktion entsteht fast sicher der Rado-Graph.

Fragestellungen

Wichtige Fragestellungen bei zufälligen Graphen sind:

Gegeben eine Eigenschaft $Q$ , für welche $p$ bzw. $m$ und ab welcher Graphengröße $n$ besitzen alle Graphen die Eigenschaft $Q$ ?

Gegeben eine Eigenschaft $Q$ , geht die Wahrscheinlichkeit für $Q$ gegen 1 oder 0 für $n\rightarrow \infty$ ? Man sagt dann auch, fast alle oder fast gar keine Graphen erfüllen die Eigenschaft $Q$ .

Wichtige Ergebnisse

Durch Anwendung der probabilistischen Methode auf sein Zufallsgraphenmodell bewies Paul Erdős den Satz: Für jede natürliche Zahl $k$ gibt es einen Graphen, bei dem sowohl Taillenweite (Länge des kürzesten Kreises) als auch Chromatische Zahl größer als k sind.^[3]

Im selben Zufallsgraphenmodell konnte gezeigt werden, dass Isomorphie zu einem beliebigen Graphen für fast alle Graphen in linearer Zeit entscheidbar ist.^[4]

Literatur

Douglas B. West: Introduction to Graph Theory. Prentice Hall, Upper Saddle River, N.J. 1996, ISBN 0-13-227828-6.

Einzelnachweise

↑ E. N. Gilbert: Random graphs, Annals of Mathematical Statistics, Band 30, 1959, S. 1141–1144
↑ P. Erdős, A. Rényi: On Random Graphs I, Publ. Math. Debrecen 6, 1959, S. 290–297
↑ Reinhard Diestel, Graphentheorie, Berlin, Heidelberg, New York: Springer, 3. Auflage 2006, S. 256ff.
↑ Babai, László, Paul Erdös, und Stanley M. Selkow. "Random graph isomorphism." Society for Industrial and Applied Mathematics Journal on Computing 9.3 (1980): 628-635. online

Basierend auf einem Artikel in:

Wikipedia.de