
Zahl 60
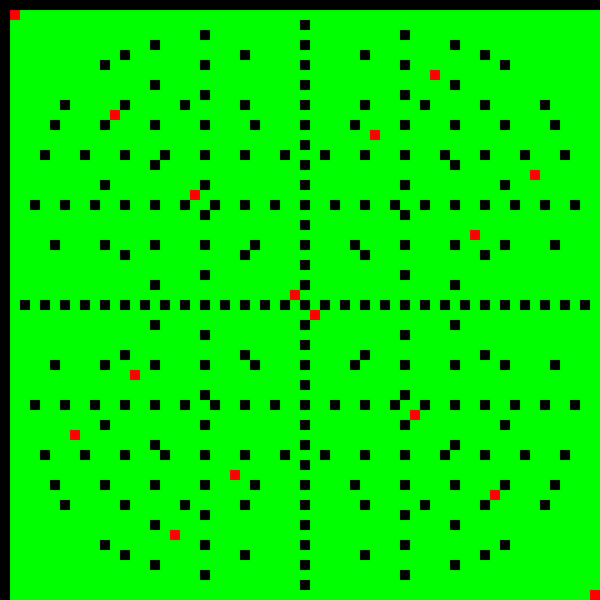
Der Restklassenring
graphisch dargestellt. Jedem der 60 Elemente von
ist eine Spalte und eine Zeile zugeordnet. Das Produkt zweier Elemente ist dann farblich an
der entsprechenden Position dargestellt, dabei steht schwarz für die Null, rot für die Eins und grün für den Rest (also 2-59). Damit lässt
sich anhand des Beispiels sofort ablesen, welche Elemente aus
invertierbar sind.
Genau die, in deren Zeile oder Spalte ein roter Punkt auftritt. Damit lässt sich dann auch sofort das inverse Element ablesen (die jeweils andere Koordinate).
Des Weiteren folgt daraus, dass in jeder Zeile und jeder Spalte mit rotem Punkt nur ein einziger schwarzer auftaucht (nämlich an erster Stelle für die Null).
Die Anzahl aller roten Punkte ist dann gerade
(siehe Eulersche φ-Funktion),
also die Anzahl der invertierbaren Elemente in
.
Da die Multiplikation in
kommutativ ist, ist das Bild symmetrisch.
Beispiele:
- Die erste Spalte und erste Zeile ist komplett schwarz, da
und
für alle x Null ist.
- Das Feld (1,1) ist rot, da
.
- Das Feld (7,43) ist auch rot, da
in
.
- Das Feld (18,4) ist grün, da
in
.
- Die 30. Spalte ist abwechselnd schwarz und grün, da
abwechselnd Null und 30 ist (für gerade x Null, für ungerade 30).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.11. 2016