
Konoid

Ein Konoid (von griechisch κωνος Kegel und -ειδης ähnlich) ist in der Mathematik eine Regelfläche, deren Erzeugendenschar (Geraden) die beiden Zusatzbedingungen
- (1) Alle Erzeugenden der Fläche sind parallel zu einer Ebene, der Richtebene.
- (2) Alle Erzeugenden schneiden eine feste Gerade, die Achse.
erfüllt.
- Das Konoid heißt gerade, falls die Achse zur Richtebene senkrecht steht.
Wegen (1) ist jedes Konoid eine Catalansche Fläche und kann durch eine Parameterdarstellung
beschrieben werden. Jede Flächenkurve
mit festem Parameter
ist eine Erzeugende,
beschreibt die Leitkurve und die Vektoren
sind alle parallel zur Richtebene. Die Planarität der Vektoren
lässt sich bei hinreichender Differenzierbarkeit durch
ausdrücken.
- Ist die Leitkurve ein Kreis, so heißt das Konoid Kreiskonoid.
Bemerkung:
- Ein Konoid ist (wie eine Gerade) unbeschränkt. Eine grafische Darstellung kann also immer nur einen endlichen Teil der Fläche zeigen.
- Der Begriff Konoid wurde bereits von Archimedes in seinem Traktat Über Konoide und Sphäroide geprägt.
Beispiele
Gerades Kreiskonoid
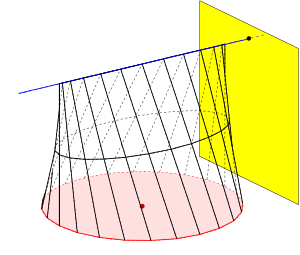
Die Parameterdarstellung
- beschreibt ein gerades Kreiskonoid mit dem Einheitskreis in der
x-y-Ebene als Leitkurve und einer zur y-z-Ebene parallelen
Richtebene. Die Achse ist die Gerade
Besonderheiten: 1) Jeder horizontale Schnitt ist eine Ellipse, 2) Die
Umrisse der im Bild gezeigten Teilfläche bzgl. der Hauptrichtungen sind ein
Rechteck, ein Kreis und ein Dreieck (s. 2. Bild), 3)
ist eine implizite Darstellung, das heißt, das gerade Kreiskonoid ist eine
Fläche 4. Grades. 4) Die Keplersche
Fassregel liefert bei einem geraden Kreiskonoid mit Grundkreisradius
und Höhe
das exakte Volumen:
.
Die implizite Darstellung wird von der ganzen Gerade
erfüllt. In den Punkten dieser Gerade existieren keine Tangentialebenen. Man
nennt solche Punkte singulär.
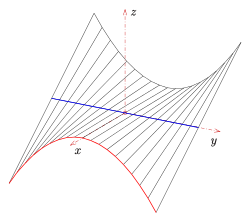
Hyperbolisches Paraboloid
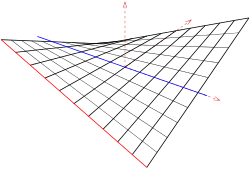
rot: Leitkurve, blau:Achse, Richtebene ist parallel zur y-z-Ebene
Die Parameterdarstellung
-
- beschreibt das hyperbolische
Paraboloid mit der Gleichung
Es ist eine Fläche 2. Grades (Quadrik).
Die Leitkurve dieses Konoids ist die Gerade
(im Bild rot), die Richtebene ist parallel zur y-z-Ebene. Wählt man die x-Achse
als Achse, ist das Konoid gerade. Da bei diesem Beispiel durch jeden
Punkt
der Fläche außer der Erzeugenden
auch die weitere Gerade
verläuft, kann man auch eine dieser weiteren Geraden als Achse wählen.
Allerdings ist nur die zuerst genannte Achse senkrecht zur Richtebene. In diesem
Fall könnte man die x-Achse sowohl als Leitkurve als auch als Achse wählen.
Das hyperbolische Paraboloid besitzt keine singulären Punkte.
Plücker-Konoid
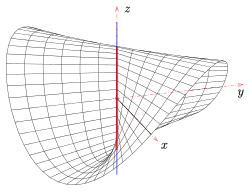
rot: Leitkurve, blau: Achse,
die Richtebene ist parallel zur x-y-Ebene
Die Parameterdarstellung
stellt ein Plücker-Konoid mit der Gleichung
dar.
Die Leitkurve ist eine zweifach durchlaufene Strecke auf der z-Achse, die Achse des Konoids ist die z-Achse und die Richtebene ist parallel zur x-y-Ebene. Da die Achse senkrecht auf der Richtebene steht, ist das Konoid gerade.
Die implizite Darstellung wird von der ganzen z-Achse erfüllt. Die Punkte der z-Achse sind singulär (es existieren keine Tangentialebenen).
Whitney Umbrella
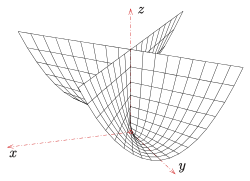
Die Parameterdarstellung
stellt einen Whitney
Umbrella mit der Gleichung
dar. Die Fläche ist ein Konoid mit der zweifach durchlaufenen positiven z-Achse
als Leitkurve, der z-Achse als Achse und einer zur x-y-Ebene
parallelen Richtebene. Da die Achse senkrecht auf der Richtebene steht,
ist auch dieses Konoid gerade.
Die implizite Darstellung wird auch von der negativen z-Achse, dem Griff des Schirms, erfüllt. Die Punkte der z-Achse sind singulär (es existieren keine Tangentialebenen).
Parabolisches Konoid
Die Parameterdarstellung
stellt ein parabolisches Konoid mit der Gleichung
dar. Das Konoid hat eine Parabel als Leitkurve, die y-Achse als
Achse und eine zur x-z-Ebene parallele Richtebene. Da die Achse
senkrecht auf der Richtebene steht, ist das Konoid gerade. Es wird in der
Architektur als Dachfläche benutzt (s. Anwendungen).
Das parabolische Konoid besitzt keine singulären Punkte.
Wendelfläche
Auch die Wendelfläche ist ein gerades Konoid. Sie besitzt keine Singularitäten.
Anwendungen
In der Mathematik
Unter den Konoiden gibt es zahlreiche einfache Beispiele von Flächen mit Singularitäten.
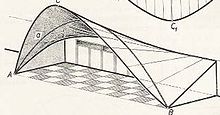
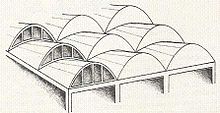
In der Architektur
Konoide finden, wie andere Regelflächen auch, in der Architektur Verwendung, da sie sich leicht aus Strecken (Balken, Stäbe) modellieren lassen. Gerade Konoide können besonders leicht hergestellt werden: Man fädelt Stäbe so auf eine Achse auf, dass sie sich nur um diese Achse drehen können. Anschließend lenkt man die Stäbe mit Hilfe einer beliebigen Leitkurve aus und erzeugt damit ein gerades Konoid. (Siehe parabolisches Konoid.)
Literatur
- Kleine Enzyklopädie Mathematik, Harri Deutsch-Verlag, 1977, S. 219.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.01. 2022