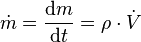Volumenstrom
| Physikalische Größe | |||||||
|---|---|---|---|---|---|---|---|
| Name | Volumenstrom (Durchfluss) | ||||||
| Formelzeichen der Größe | 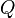 | ||||||
| |||||||
| Siehe auch: Fluss (Physik), Massenstrom | |||||||
Der Volumenstrom (oder ungenauer Durchflussrate) ist eine physikalische Größe aus der Fluidmechanik. Sie gibt an wie viel Volumen eines Mediums pro Zeitspanne durch einen festgelegten Querschnitt transportiert wird. Zumeist ist das Medium ein Fluid (Flüssigkeit oder Gas). Die SI-Einheit des Volumenstroms ist m³/s, gebräuchlich sind je nach Größenordnung des Volumenstroms auch viele andere Einheiten. Beispielsweise ml/min (200 ml/min Blut fließen durch die innere Halsschlagader des Menschen) oder m³/h (Im Mittel fließen 1 Million m³/h Erdgas durch die Nord Stream Pipeline). Der Volumenstrom wird mittels Durchflussmessern gemessen.
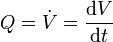
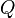 :
Volumenstrom
:
Volumenstrom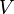 :
Volumen
:
Volumen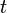 :
Zeit
:
Zeit
Zusammenhang mit Strömungsgeschwindigkeit
Der Volumenstrom 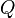 hängt mit der mittleren Strömungsgeschwindigkeit
hängt mit der mittleren Strömungsgeschwindigkeit 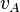 durch die Querschnittsfläche
durch die Querschnittsfläche 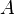 zusammen über die Beziehung:
zusammen über die Beziehung:
-
-
 Skizze zur Erklärung eines Strömungprofils. In einer Rohrleitung ist die Strömungsgeschwindigkeit einzelner Stromfäden über den Querschnitt nicht konstant. An der Rohrwand ist die Strömungsgeschwindigkeit null und bei ungestörten Strömungen in der Mitte maximal. Die Form des Strömungsprofils hängt von der Reynoldszahl ab.
Skizze zur Erklärung eines Strömungprofils. In einer Rohrleitung ist die Strömungsgeschwindigkeit einzelner Stromfäden über den Querschnitt nicht konstant. An der Rohrwand ist die Strömungsgeschwindigkeit null und bei ungestörten Strömungen in der Mitte maximal. Die Form des Strömungsprofils hängt von der Reynoldszahl ab.
-
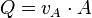 .
.
Mit dieser Formel lässt sich bei bekannter Querschnittsfläche (Rohre, Kanäle) der Volumenstrom errechnen, wenn die Fließgeschwindigkeit am durchströmten Querschnitt bekannt ist.
Die Strömungsgeschwindigkeit in einem Querschnitt ist im Allgemeinen nicht konstant über den Querschnitt (siehe Darstellung), für laminare Strömung ergibt sich die mittlere Strömungsgeschwindigkeit allgemein zu

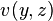 :
Geschwindigkeit an der Stelle (y,z) des Querschnitts, mit Strömung in
x-Richtung.
:
Geschwindigkeit an der Stelle (y,z) des Querschnitts, mit Strömung in
x-Richtung.
Kontinuitätsgesetz
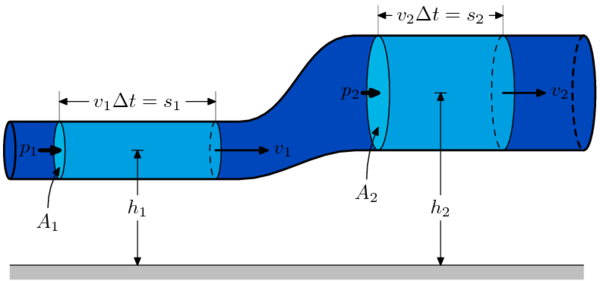
Bei sich änderndem Querschnitt gilt für Strömungen inkompressibler Fluide das Kontinuitätsgesetz:
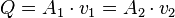 .
.
Dabei ist 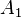 der Querschnitt, an dem das Fluid mit einer mittleren Geschwindigkeit von
der Querschnitt, an dem das Fluid mit einer mittleren Geschwindigkeit von 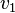 strömt. Ändert man den Querschnitt zu
strömt. Ändert man den Querschnitt zu 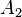 ,
so ändert sich die mittlere Strömungsgeschwindigkeit zu
,
so ändert sich die mittlere Strömungsgeschwindigkeit zu 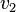 .
Anders ausgedrückt: Der Volumenfluss ist eine Erhaltungsgröße
für Flüssigkeiten bei Querschnittsänderungen der Strömung.
.
Anders ausgedrückt: Der Volumenfluss ist eine Erhaltungsgröße
für Flüssigkeiten bei Querschnittsänderungen der Strömung.
Flüssigkeiten sind in erster Näherung inkompressibel, d. h. ihre Dichte ändert sich nicht, wenn man den Strömungsquerschnitt bei konstantem Volumenfluss aufweitet oder einschnürt (und somit den Druck ändert). Für Gase gilt dies dagegen nicht.
Zusammenhang mit Massenstrom
Der Massenstrom 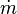 hängt über
hängt über
mit dem Volumenstrom zusammen, falls die Dichte
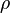 über den Querschnitt konstant ist. Sonst muss dieses Produkt über den
Querschnitt integriert werden.
über den Querschnitt konstant ist. Sonst muss dieses Produkt über den
Querschnitt integriert werden.
Normvolumenstrom
Das Volumen einer gegebenen Stoffmenge Gas ist abhängig von Druck und Temperatur. Da beide Größen in Rohrleitungsnetzen oder industriellen Prozessen nicht konstant sind, wird der Volumenstrom von Gasen oft als Normvolumenstrom angegeben. Dazu wird das in einer bestimmten Zeitspanne gemessene Volumen (Betriebsvolumen) auf ein Normvolumen mit festgelegtem Druck und Temperatur umgerechnet. Es gilt
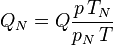 ,
,
dabei sind 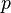 und
und 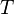 tatsächlich vorherrschender Druck und Temperatur während der
Betriebsvolumenmessung und
tatsächlich vorherrschender Druck und Temperatur während der
Betriebsvolumenmessung und 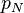 und
und  Druck und Temperatur der Normbedingungen
(beispielsweise
Druck und Temperatur der Normbedingungen
(beispielsweise 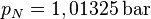 und
und 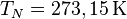 ,
die Normbedingungen variieren weltweit und umfassen auch noch weitere
Bedingungen wie Luftfeuchte).
Hierbei müssen
,
die Normbedingungen variieren weltweit und umfassen auch noch weitere
Bedingungen wie Luftfeuchte).
Hierbei müssen 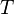 und
und  als absolute
Temperatur verstanden werden. Diese hängt mit der Celsius-Temperatur
als absolute
Temperatur verstanden werden. Diese hängt mit der Celsius-Temperatur 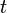 wie folgt zusammen:
wie folgt zusammen: 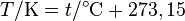 .
.
Bezeichnungen
- In manchen Bereichen der Naturwissenschaft und Technik werden Volumenströme kurz als -fluss bezeichnet, z.B. der Abfluss in der Hydrologie. In Technik und Wirtschaft kann auch ein Brennstoffdurchsatz oder eine Fördermenge als Volumenstrom angegeben sein.


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 16.11. 2023