Dilatanz (Fluid)

Dilatanz (von lateinisch dilatus verzögernd, aufschiebend, hinhaltend, schleppend, Part. Perf. von differre), auch Scherverzähung, ist in der Rheologie die Eigenschaft eines nichtnewtonschen Fluids, bei hohen zeitlichen Änderungen der Scherung (d.h. bei hoher Schergeschwindigkeit) eine höhere Viskosität zu zeigen. Im Englischen nennt man ein dilatantes Fluid auch shear-thickening, also „scherverdickend“ oder „scherverfestigend“.

Die Zunahme der Viskosität entsteht durch eine Strukturänderung im Fluid, die dafür sorgt, dass die einzelnen Fluid-Partikel stärker miteinander wechselwirken (z.B. sich verhaken) und so schlechter aneinander vorbei gleiten. Für konzentrierte Suspensionen lässt sich Dilatanz als scherinduzierter Phasenübergang beschreiben.

Die Viskosität (Zähigkeit) eines dilatanten Fluids steigt also mit der Schergeschwindigkeit, hängt aber bei konstanter Schergeschwindigkeit nicht von der Zeit ab. Wenn die Viskosität dagegen nach Verminderung der Scherkraft nicht sofort, sondern zeitabhängig wieder absinkt, spricht man von Rheopexie.

Mathematisch-Physikalische Modellierung

Abbildung 3: Schubspannungs-Schergeschwindigkeits-Diagramm:
1: Scherverzähendes (dilatantes) Fluid
2: Newtonsches Fluid
3: Scherverdünnendes (pseudoplastisches) Fluid
4: Bingham-plastisches Fluid
5: Casson-plastisches Fluid
Nach rechts ist die Schergeschwindigkeit und nach oben die daraus resultierende Schubspannung angetragen.

Trägt man die Schubspannung $\,\tau$ als Funktion der Schergeschwindigkeit (Scherrate) $\,{\frac {du}{dy}}$ auf, so sind Flüssigkeiten mit Dilatanz typischerweise gekennzeichnet durch ein Fließgesetz der Form

$\,\tau =K\left({\frac {du}{dy}}\right)^{n}$

mit

dem Konsistenz-Faktor K
dem Fließindex n > 1 (Kurve 1 im Diagramm).

Das gegensätzliche Verhalten, die Abnahme der Viskosität mit der Scherrate bzw. Schubspannung, entsprechend einem Index n < 1, wird Strukturviskosität (auch Scherentzähung, Scherverdünnung) genannt und findet sich z.B. in hochpolymeren Lösungen (Kurve 3 im Diagramm).

Für Newtonsche Flüssigkeiten wie Wasser ist n = 1, die Viskosität also unabhängig von Schubspannung oder Scherrate (Kurve 2 im Diagramm).

Beispiele

Bei einem Stärkebrei kann man das Verhalten im Experiment gut beobachten: dazu wird Stärke mit Wasser verrührt, so dass ein wässriger Brei entsteht. Wenn man einen Löffel langsam durch den Brei zieht, erscheint dieser flüssig, bei höherer Geschwindigkeit wird der Brei so zäh, dass er nicht mehr fließt, sondern eher wegbröckelt. Die Bröckchen werden jedoch nach sehr kurzer Zeit wieder flüssig und verschmelzen mit dem übrigen Brei. Dieses Verhalten ist ein Beispiel für Dilatanz, aber nicht für Rheopexie.
Auch Kochkäse verhält sich dilatant: Er lässt sich langsam rühren, wird bei höherer Geschwindigkeit aber fester und reißt.
Zinkpasten mit einem hohen Feststoffanteil weisen ebenfalls Dilatanz auf. Das kann zum Festsetzen der Salbenmühle führen, mit der diese Paste hergestellt wird, und muss entsprechend beachtet werden.
Suspensionen feiner Teilchen in Beton (Beton-Suspensionen) weisen ebenfalls die Eigenschaften einer dilatanten Flüssigkeit auf.

Verwendung

Der US-Hersteller Dow Corning produziert aus Silikon-Polymer den dilatanten hüpfenden Kitt, der bisher vor allem als Kinderspielzeug auf dem Markt war. Neben der normalen Knetbarkeit verhält sich diese Substanz bei plötzlicher, mechanischer Belastung völlig anders: wirft man eine Kugel aus dem Material zu Boden, springt sie wie ein Gummiball zurück; schlägt man mit dem Hammer sehr schnell auf ein Stück, zerspringt dieses in viele kleine scharfkantige Stücke, fast wie Keramik. Auch beim Zerreißen bilden sich scharfe Kanten und glatte Bruchflächen. Technische Anwendungen sind nicht bekannt.

Ein Material mit ähnlichen Eigenschaften wird seit kurzem als Active Protection System (APS) beispielsweise in Motorradbekleidung eingesetzt: speziell geformte Polster, die einen dilatanten Verbundwerkstoff enthalten, erlauben die freie Beweglichkeit des Trägers. Bei einem abrupten Schlag infolge eines Sturzes jedoch „verhärtet“ das Material zu einer hartgummiähnlichen Konsistenz, verteilt die einwirkenden Kräfte auf eine größere Körperpartie und verhindert so Verletzungen.

Aktuell werden dilatante Flüssigkeiten in Verbindung mit Kevlargeweben bei der Herstellung von Schuss- bzw. stichfesten Schutzwesten erprobt. Das Gewebe erhält durch die Tränkung mit der Flüssigkeit eine derart hohe Widerstandskraft gegenüber dem Eindringen, dass sogar metallische Pfeilspitzen, abgeschossen von schweren Jagdpfeilbögen, ein wenige Millimeter dickes Gewebe nicht zu durchdringen vermögen.

Erklärung als scherinduzierter Phasenübergang

Es gibt verschiedene Erklärungsansätze für Dilatanz in konzentrierten Suspensionen kolloidaler (Brownscher) Teilchen. Hier wird der Ansatz näher erläutert, Dilatanz als scherinduzierten Phasenübergang zu betrachten.

Zwei-Teilchen-Potential elektrisch stabilisierter kolloidaler Teilchen.

Ausgangspunkt für die Erklärung von Dilatanz in konzentrierten Suspensionen sind die zwischenmolekularen Kräfte kolloidaler Teilchen. Die Wechselwirkung elektrisch stabilisierter kolloidaler Partikel wird durch die DLVO-Theorie beschrieben. Sie zeichnet sich durch zwei entgegengesetzt wirkende Kräfte aus. Einerseits werden die Teilchen durch Van-der-Waals-Kräfte angezogen. 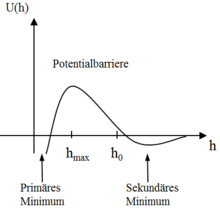Andererseits befinden sich auf den Teilchen und um sie herum Ladungen (elektrische Doppelschicht), die dazu führen, dass sich kolloidale Teilchen gegenseitig abstoßen. In der Grafik ist das zwei-Teilchen Potential U(h) elektrisch stabilisierter Partikel schematisch dargestellt. Es besteht aus einem primären und sekundären Minimum, verursacht durch die van der Waals Anziehung, und einem Potentialwall aufgrund der elektrostatische Abstoßung, dessen Maximum sich bei $h_{\mathrm {max} }$ befindet.

Erhöht man beispielsweise die Konzentration der Teilchen in einer Suspension, so wird der gegenseitige Abstand $h_{0}$ immer kleiner. Ab einer bestimmten kritischen Konzentration reichen thermische Fluktuationen (Brownsche Bewegung) aus, den Potentialwall zu überwinden. Die kolloidale Suspension wird instabil, d. h. die Brownschen Teilchen koagulieren und haften aufgrund der Van-der-Waals-Anziehung aneinander. Damit verbunden ist die Trennung in zwei Phasen, einer konzentrierten (koagulierten) Phase und einer Phase nahezu ohne Teilchen. Gleiches kann man erreichen, indem man die elektrostatische Abstoßung beispielsweise durch Hinzufügen geeigneter Ionen (Salz) verringert. Die Suspension zeigt in beiden Fällen einen Gleichgewichts-Phasenübergang von einem sogenannten kolloidalen Fluid in einen kolloidalen Festkörper.

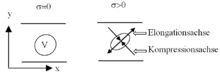
Die Zunahme der Teilchenkonzentration ist gleichbedeutend mit einer Verringerung des Volumens pro Teilchen. Aus makroskopischer Sicht sollte eine Scherung, bei der das Volumen eines Flüssigkeitselements erhalten bleibt, keinen Effekt hervorrufen. Die makroskopische Sicht vernachlässigt jedoch die granulare Struktur einer Suspension bestehend aus festen Teilchen. Um ein Verständnis für Dilatation in Suspensionen zu bekommen, muss man auf die mesoskopische Ebene wechseln. Dazu sei eine kugelförmige Dichtefluktuation aus einer großen Anzahl kolloidaler Teilchen betrachtet, wie in der Grafik schematisch dargestellt.

Scherung einer Dichtefluktuation mit dem Volumen V in x-Richtung mit dem Scherstress σ.

Diese wird während ihrer Lebensdauer $\tau$ durch eine kontinuierliche Scherung mit der Schergeschwindigkeit $\gamma$ um den Wert deformiert:

${\begin{aligned}u&=\tau \gamma \end{aligned}}$

Mit zunehmenden Volumenfraktionen wächst die Lebensdauer τ einer Dichtefluktuation und wird schließlich in der Nähe der sogenannten dichtesten Kugelpackung unendlich (Lubrikationstheorie). Anders gesagt, eine Suspension verhält sich mit zunehmender Konzentration kolloidaler Teilchen wie ein Festkörper. Für den Fall einer kontinuierlichen Scherdeformation wird eine Dichtefluktuation während ihrer Lebensdauer wie in der Grafik dargestellt in die Länge gezogen (Elongationsachse) und gleichzeitig senkrecht dazu komprimiert (Kompressionsachse). Kolloidale Teilchen nähern sich dabei entlang der Kompressionsachse an. Die Teilchen können bei genügend großer Scherdeformation sich so nahe kommen, dass sie die Potentialbarriere überwinden. Wenn das passiert, bleiben sie aneinander haften und erhöhen damit die Scherviskosität.

Betrachtet man diesen Effekt als einen Aktivierungsprozess, kann man sowohl den Gleichgewichts- als auch den scherinduzierten Phasenübergang mit einer einfachen Formel näherungsweise berechnen. Bezeichnen wir die Anzahl von Koagulationsereignissen pro Zeiteinheit mit dann ist sie durch die Boltzmann-Statistik gegeben durch:

$f=f_{0}\exp \left({\frac {U_{B}-\sigma V}{k_{\mathrm {B} }T}}\right)$

wobei $\sigma$ der angelegte Scherstress, das Aktivierungsvolumen und $k_{\mathrm {B} }T$ die thermische Energie ist. Die Frequenz hat den maximalen Wert $f_{0}$ , wenn der Exponent gerade verschwindet. Für $\sigma =0$ ist der Gleichgewichts-Phasenübergang bestimmt durch das Maximum der Potentialbarriere $U_{B}=U(h_{\mathrm {max} })$ . Für $\sigma >0$ lässt sich der kritische Scherstress $\sigma _{C}$ für das Auftreten der Dilatanz bestimmen durch:

$\sigma _{C}={\frac {U_{B}}{V}}$

Die Betrachtung der Dilatanz als scherinduzierten Phasenübergang erlaubt die Berechnung und Erklärung experimenteller Resultate:

Dilatanz verschwindet bei niedrigen Volumenfraktionen. Da die Lebensdauer $\tau$ von Dichtefluktuation bei niedrigen Volumenfraktionen sehr klein ist, verschwinden diese, bevor sie ausreichend deformiert werden können.
Es gibt zwei Formen von Dilatanz: reversible und irreversible Dilatanz. Bei der irreversiblen Dilatanz können sich einmal geformte Teilchencluster nicht wieder voneinander trennen, weil sie im primären Potentialminimum gefangen sind. Im reversiblen Fall kommen sich die kolloidalen Teilchen, verursacht durch die Oberflächenrauigkeit, nicht nahe genug, um nicht von thermischen Anregungen wieder getrennt zu werden. Dieser Prozess dauert allerdings eine gewisse Zeit und führt zur Rheopexie.
Dilatation kann durch geeignete Wahl der Teilchen und deren Wechselwirkung (Volumenfraktion, Salzkonzentration, suspendierendes Medium etc.) beeinflusst werden. Die Gleichung für den kritischen Stress legt nahe, dass dieser geringer wird je niedriger das Potentialmaximum $U_{{B}}$ , also je näher eine Suspension einem Gleichgewichtsphasenübergang ist. Erhöht man beispielsweise die Volumenkonzentration oder den Salzgehalt einer elektrisch stabilisierten Suspension, so verringern sich die Schergeschwindigkeiten bzw. der Scherstress um Dilatation auszulösen.
Bereits koagulierte Suspensionen zeigen keine Dilatanz, sondern lediglich Scherverdünnung.

Literatur

Rheologie Normen. Beuth Verlag, 2007, ISBN 3-410-16576-2. (speziell DIN 1342-1)

Basierend auf einem Artikel in:

Wikipedia.de