
Staudruck
Der Staudruck ist der dynamische Druck und entspricht der Erhöhung des Drucks am Staupunkt eines umströmten Körpers gegenüber dem statischen Druck des Fluids. Mit Hilfe des Staudrucks kann die Geschwindigkeit gegenüber dem Fluid ermittelt werden.
Messung
Zur Messung des Staudrucks muss der statische Druck vom Druck am Staupunkt (Gesamtdruck) abgezogen werden. Dies kann durch eine getrennte Messung des statischen Drucks gefolgt von einer rechnerischen Subtraktion geschehen. Eine andere Möglichkeit besteht darin, einen Differenzdrucksensor zu verwenden, bei dem die Differenz auf physikalische Weise gebildet wird. Dem Sensor wird mit Schläuchen der lokale Druck am Staupunkt und an einer Fläche senkrecht zu Anströmung zugeführt.
Der Staupunkt, an dem gemessen wird, sollte möglichst ungestört angeströmt werden. Daher wird in Flugzeugen ein Staurohr verwendet, dessen Öffnung ein Stück weit vor den Bug oder vor das Leitwerk ragt. Eine spezielle Bauform, bei der die Öffnungen für die Druckmessungen so gelegt sind, dass sich ein müglichst geringer Messfehler bei schräger Anströmung ergibt, ist die Prandtlsonde.
Mathematische Beschreibung
Die Strömgeschwindigkeit sei 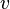 ,
der statische Druck
,
der statische Druck 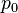 ,
die Dichte des strömenden Mediums
,
die Dichte des strömenden Mediums 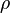 .
(
.
(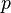 in N/m2;
in N/m2; 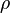 in kg/m3;
in kg/m3; 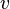 in m/s)
in m/s)
Der Staudruck 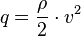 und der Totaldruck am Staupunkt
und der Totaldruck am Staupunkt 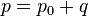
mit
-
dem Totaldruck
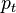 am Staupunkt
am Staupunkt - der Dichte
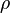 des strömenden Mediums
des strömenden Mediums - der Strömungsgeschwindigkeit
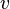 .
.
Prantlsonde

Die Prandtlsonde (benannt nach Ludwig Prandtl), auch Prandtl'sches Staurohr genannt, ist ein strömungstechnisches Messinstrument zur Bestimmung des Staudrucks. Es stellt eine Kombination aus Pitotrohr und statischer Drucksonde dar. Das Prandtlrohr hat eine Öffnung in Strömungsrichtung zur Messung des Gesamtdruckes und ringförmig in einem wohlberechneten Abstand zur Spitze und zum Schaft seitliche Bohrungen für die statische Druckmessung. Die Differenz dieser beiden Drücke entspricht nach dem Gesetz von Bernoulli dem dynamischen Druck (Staudruck). Der Staudruck kann durch ein Manometer direkt bestimmt werden, alternativ lässt sich über den Staudruck auch die Geschwindigkeit der die Sonde umströmenden Luft errechnen. Dies ist wichtig in der Luftfahrt zur Bestimmung der Luftgeschwindigkeit (vgl. True Airspeed). Die Prandtlsonde ist dabei meist Teil eines Pitot-Statik-Systems.
Zur Bestimmung der Luftgeschwindigkeit verwendet man ein Leitungssystem, in
dem sich eine Flüssigkeit befindet.
Auf dieses Fluid wirkt eine Kraft 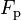 ,
welche durch den Unterschied zwischen statischem und Staudruck entsteht.
,
welche durch den Unterschied zwischen statischem und Staudruck entsteht.
Die Prandtlsonde wird so in eine Luftströmung eingebracht, dass die Strömung
senkrecht auf die vordere Öffnung trifft. Der sich aus dieser Anordnung
ergebende Druck am Staupunkt 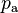 besteht aus der Summe zwischen statischen
besteht aus der Summe zwischen statischen 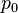 und dynamischen Druck
und dynamischen Druck 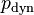 auch Staudruck genannt. Nach der Bernoulli'schen
Gleichung ergibt sich:
auch Staudruck genannt. Nach der Bernoulli'schen
Gleichung ergibt sich:
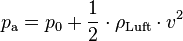
Weitere Öffnungen der Sonde sind so positioniert, dass an ihnen die Luft ohne sich zu stauen, vorbei strömt. Im Inneren der Sonde herrscht demnach nur der statische Druck und es gilt:
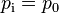
Aus dem Druck innerhalb und außerhalb des Staurohrs ergibt sich eine
Druckdifferenz 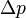 die nur aus dem dynamischen Anteil des Drucks besteht:
die nur aus dem dynamischen Anteil des Drucks besteht:
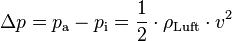
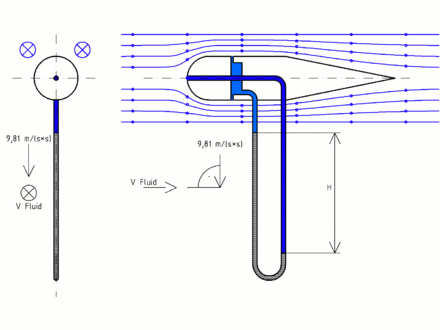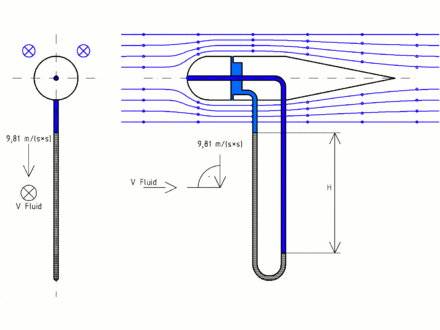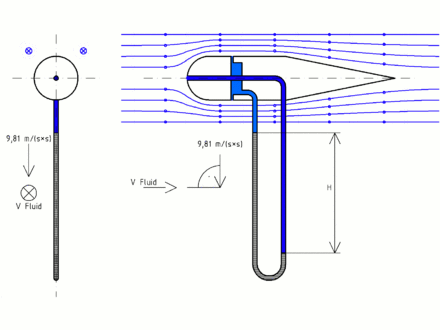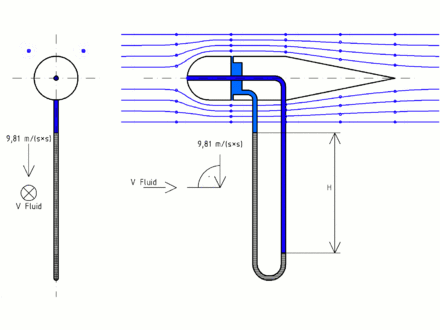
Die physikalische Verwirklichung der Differenzmessung ist in der schematischen Darstellung des Staurohrs skizziert. Ein Rohr dient als Verbindung zwischen dem Staupunkt und den seitlichen Öffnungen. Zur Messung wird eine Flüssigkeit eingebracht. Entsprechend wirkt auf die Flüssigkeit in diesem Rohr eine Kraft von
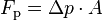
wobei 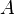 die Querschnittsfläche des Rohrs ist. Durch diese Kraft wird die
Flüssigkeitssäule im Rohr verschoben. Sobald eine Höhendifferenz von
die Querschnittsfläche des Rohrs ist. Durch diese Kraft wird die
Flüssigkeitssäule im Rohr verschoben. Sobald eine Höhendifferenz von 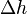 erreicht ist, wirkt die Gravitationskraft
dem Prozess entgegen: Eine Masse von
erreicht ist, wirkt die Gravitationskraft
dem Prozess entgegen: Eine Masse von
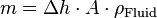
bewirkt eine Kraft von
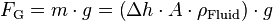
Es stellt sich ein Kräftegleichgewicht ein:
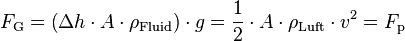
Diese Gleichung lässt sich zur Bestimmung der Geschwindigkeit 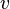 heranziehen:
heranziehen:
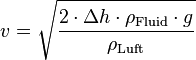
Kielsonde

Die Kielsonde, auch Kielsches Rohr genannt, ist eine Weiterentwicklung des Pitotrohres und ist nach seinem Erfinder Georg Kiel, einem NACA-Mitarbeiter, benannt. Es dient der Messung des Totaldrucks in bewegten Strömungen und hat gegenüber dem normalen Pitotrohr den Vorteil, dass es eine geringere Sensitivität bezüglich des Anströmwinkels aufweist.
Aufbau und Funktionsweise
Die Kielsonde besteht im Wesentlichen aus einer Venturidüse, in deren Inneren sich eine Pitotsonde befindet. Die Venturidüse lenkt dabei die Strömung in Axialrichtung um und sorgt somit für eine konstantere Anströmung der Pitotsonde. Wesentlich für die Güte der Messanordnung ist die Geometrie des Einlaufs. Neben Rundungsradius des Einlaufs, Rampenwinkel und Durchmesserverhältnis der Venturidüse spielt auch die Position der Pitotsonde in Axialrichtung eine wesentliche Rolle für die Sensitivität bezüglich des Anströmwinkels. Machzahl-abhängig werden gute Messergebnisse bis zu Anströmwinkeln über 60° relativ zur Symmetrieachse erreicht.

© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.09. 2017