Bitfehlerhäufigkeit

Die Bitfehlerhäufigkeit (BFH) ist ein Begriff der Nachrichtentechnik für die Qualität der Übertragung über einen Kanal oder eine digitale Übertragungsstrecke.

Der Begriff der Bitfehlerquote

In den Normen gilt als der korrekte Ausdruck für die gemeinte Größe die Bitfehlerquote: In Electropedia, dem Wörterbuch der Internationalen Elektrotechnischen Kommission IEC, ist diese Größe in Definition 702-07-39 definiert als die Anzahl der in einem beliebigen Zeitintervall fehlerhaft empfangenen Bits (Bitfehler) geteilt durch die Anzahl der im gleichen Zeitintervall insgesamt empfangenen Bits. Handelt es sich um gespeicherte Bits auf einem Speichermedium, so wird nicht ein definiertes Zeitintervall zugrunde gelegt, sondern eine definierte Speichergröße. Beispiel: Eine Bitfehlerquote von 3·10⁻⁶ bedeutet, dass von 1 Million übertragener oder gespeicherter Bits durchschnittlich 3 Bits falsch sind.

Die Messung zur Ermittlung der Bitfehlerquote auf Übertragungsstrecken wird gewöhnlich mit Hilfe von Testsignalen (also Prüfbitmustern) durchgeführt, die von einem Messgerät gesendet werden.

Bitfehlerwahrscheinlichkeit

Im Gegensatz zur Bitfehlerrate beschreibt die Bitfehlerwahrscheinlichkeit (engl. bit error probability) eine durch theoretische Überlegungen berechnete Wahrscheinlichkeit für das Auftreten eines Bitfehlers. Geschlossene Berechnungen von Bitfehlerwahrscheinlichkeiten sind meist nur für idealisierte Szenarien möglich, werden aber häufig verwendet, um aufwendige Simulationen zu ersetzen und Grenzen der Leistungsfähigkeit von nachrichtentechnischen Systemen zu bestimmen.

Excessive Bit Error Ratio und Signal Degraded

Excessive Bit Error Ratio (auf deutsch: sehr hohe Bitfehlerquote) ist eine Fehlerdefinition, die in der Synchronen Digitalen Hierarchie und der Plesiochronen Digitalen Hierarchie verwendet wird. Die Sekunden, in denen mindestens eine „sehr hohe Bitfehlerquote“ aufgetreten ist, werden gewöhnlich in einem MIB aufgezeichnet und gezählt. Mit solchen Zählern kann die Qualität einer Datenkommunikation während der Benutzungszeit definiert gemessen werden.

Eine ähnliche Definition ist Signal degraded (SD). Die Fehlerschwelle von „Signal degraded“ wird gewöhnlich bei 1 Bitfehler auf 1 Million übertragene Bits erreicht. Für Standleitungen in Deutschland ist der Fehler „Excessive Bit Error Ratio“ das vertragsmäßig festgelegte Kriterium für einen Ausfall der Standleitung.

Verwechslungsmöglichkeiten

Vielfach wird noch der Ausdruck „Bit error rate“ verwendet; das wäre die Anzahl der Bitfehler je Zeiteinheit. Das hat wenig Aussagekraft. Aber sowohl für „bit error rate“ wie für „bit error ratio“, also Bitfehlerquote, wird die Abkürzung „BER“ verwendet. Um Verwechslung zu vermeiden, sollte die Abkürzung BER ganz vermieden werden.

Messverfahren

Das Messen der Bitfehlerquote erfordert eine hochwertige Bezugsinformation bzw. eine verlässliche Bezugsgröße. Das können beispielsweise sein

ein Vergleich einer mitempfangenen Prüfinformation,
eine idealisierte modellhafte Sollinformation,
eine Bewertung des empfangenen Leistungsspektrums,
eine Bewertung gegenüber einem bekannten Prüfsignal, vergleiche den schon genannten Artikel „Pseudozufallsfolgen für Testsignale“.
eine fehlerfreie unabhängige Referenzinformation oder
ein Vergleich über eine hinreichend lange Messdauer mit wiederkehrenden Informationen.

Beispiel

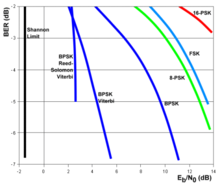
Bitfehlerhäufigkeit als Funktion von Eb/N0

Bezieht man das Signal-Rausch-Verhältnis auf ein Informationsbit, so erhält man das Bitenergie-Rauschleistungsdichte-Verhältnis $\frac{E_b}{N_0}$ , das Verhältnis der für ein Informationsbit aufgewendeten Energie E_b zur spektralen Rauschleistungsdichte N₀. Mit steigendem Rauschen, d.h. abnehmendem Eb/N0, steigt die Bitfehlerquote.

Weiterhin hängt die BER vom Codierverfahren ab: 16-PSK oder 8-PSK besitzen eine höhere Informationsdichte als beispielsweise 2-PSK und benötigen einen höheren Signal-Rauschabstand. Vorwärtsfehlerkorrekturverfahren senken die erforderliche Signalgüte zur sicheren Übertragung eines Datenwortes.

Die Abbildung zeigt für verschiedene leistungsbegrenzte Codierverfahren die Fehlerhäufigkeit in Abhängigkeit von Eb/N0 (dargestellt in dB). Beispielsweise beträgt bei einem Bitfehlerverhältnis von 10⁻⁴ das Verhältnis Eb/N0 für BPSK etwa 8 dB, mit der FEC-Kodierung Faltungscodes decodiert mit dem Viterbi-Algorithmus etwa 4 dB. Eine zusätzliche Reed-Solomon-Kodierung reduziert das minimal benötigte Eb/N0 auf weniger als 3 dB. Die senkrechte Linie in der Abbildung kennzeichnet das Shannon-Limit, das nicht unterschritten werden kann.

Literatur

Herbert Bernstein: Messen mit dem Oszilloskop. Praxisnahes Lernen mit einem PC-Simulationsprogramm, 2. Auflage, Springer Fachmedien, Wiesbaden 2016, ISBN 978-3-658-15100-3.
Karl Steinbuch, W. Weber (Hrsg.): Taschenbuch der Informatik. Band III, Anwendungen und spezielle Systeme der Nachrichtenverarbeitung, Springer Verlag, Berlin / Heidelberg 1974, ISBN 978-3-642-65589-0.
Herbert Bernstein: Informations- und Kommunikationselektronik. De Gruyter Verlag, Oldenburg 2015, ISBN 978-3-11-036029-5.
Peter Gerdsen: Digitale Übertragungstechnik. B. G. Teubner Verlag, Stuttgart 1983, ISBN 978-3-519-00093-8.
Peter Welzel: Datenfernübertragung. Einführende Grundlagen zur Kommunikation offener Systeme, Friedrich Vieweg & Sohn Verlag, Wiesbaden 1986, ISBN 978-3-663-00129-4.

Basierend auf einem Artikel in:

Wikipedia.de