Blockcode

Systematischer Blockcode aus voneinander getrennten Informations- und Prüfsymbolen

Blockcodes sind eine Art der Kanalkodierung der Familie der (fehlererkennenden und) fehlerkorrigierenden Codes. Sie zeichnen sich durch eine feste Blockgröße aus Symbolen eines festen Alphabets $\Sigma$ (bei Binärcodes $\Sigma =\{0,1\}$ ) aus. Einzelne Blocks werden im Gegensatz zu Faltungscodes unabhängig voneinander kodiert und dekodiert.

Wichtige Eigenschaften eines Blockcodes sind die Informationsrate (das Verhältnis aus enthaltener Informationsmenge zur Gesamt-Datenmenge ) sowie seine Korrekturrate (d.h. die Fähigkeit Fehler zu erkennen und/oder zu korrigieren). Beide Eigenschaften beeinflussen einander gegenseitig und spannen eine gemeinsame, unüberwindbare Schranke auf. Durch Optimierung kann man sich der Schranke nähern, erhält aber lange und aufwändig zu dekodierende Codes. Hier hat sich das Kaskadieren von Codes als praktikablere Lösung erwiesen.

Obwohl Blockcodes häufig nicht optimal im Sinne einer minimalen mittleren Codewortlänge sind, schränkt man sich oft auf Blockcodes ein. Eine weitere Spezialisierung stellen lineare Codes und systematische Codes dar.

Aufbau

Aus dem Alphabet $\Sigma$ und der Blockgröße ergeben sich $\Sigma ^{n}$ mögliche Worte, von denen eine Teilmenge ${\mathcal {C}}\subseteq \Sigma ^{n}$ die gültigen Codeworte darstellt. Die Mächtigkeit des Alphabets $\Sigma$ wird mit $q=|\Sigma |$ bezeichnet, sie beträgt im Falle von Binärcodes $q=|\Sigma |=2$ . Die Mächtigkeit des Codes $|{\mathcal {C}}|$ kann bei vielen Codes (bei linearen Codes immer) als $|{\mathcal {C}}|=q^{k}$ mit $k\in \mathbb {N} ^{+}$ geschrieben werden. Diese Codes können bei einer Blockgröße von Symbolen eine Nutzlast $k \leq n$ tragen.

Die Informationrate beträgt $k/n\leq 1$ , die Korrekturrate wird durch den (minimalen) Hamming-Abstand des Codes ${\mathcal {C}}$ limitiert. Der Hamming-Abstand zweier Codeworte $c_{i}$ und $c_{j}$ ist hierbei die Anzahl unterschiedlicher Symbole dieser Codeworte $\Delta (c_{i},c_{j})$ , der (minimale) Hamming-Abstand eines (ganzen) Codes ${\mathcal {C}}$ ist der minimale Hamming-Abstand aller (disjunkten) Codewort-Paare, d.h. $d=\Delta ({\mathcal {C}})\,\,{\overset {\underset {\mathrm {def} }{}}{=}}\,\min _{i\neq j}\,\Delta (c_{i},c_{j})$ . Letztere beschränkt die maximale (zuverlässige) Korrekturleistung auf Symbolfehlern mit $t=\left\lfloor (d-1)/2\right\rfloor$ ein. Bei kaskadierten Korrekturverfahren spielt neben der Fehlerkorrektur auch die Fehlererkennung eine Rolle. Zum einen erkennen Nicht-perfekte Codes eine gewisse Menge an Mehrbit-Fehler mit $t_{\mathrm {Mehrbit} }>t$ , die sie selbst nicht mehr korrigieren können, zum anderen kann man Fehlerkorrektur-Fähigkeiten gegen weitere (garantierte) Fehlererkennungs-Fähigkeiten eintauschen und damit folgende Korrektur-Stufen unterstützen: $r=d-1-t_{\mathrm {benutzt} }$ .

Für Codes haben sich in der Literatur unterschiedliche Notationen etabliert:

$[n,k;d,q]$ oder $[n,k;d]_{q}$ , häufig wird das Semikolon durch ein Komma ersetzt, die eckigen Klammern durch runde Klammern. $q=2$ wird häufig weggelassen, gleiches gilt für das $d=3$ der klassischen Hamming-Codes.
Häufig wird statt (der Anzahl der Nutzsymbole) die Mächtigkeit des Codes $q^{k}=|{\mathcal {C}}|$ , d.h. $(n,q^{k},d)_{q}$ oder der Code selbst angegeben $(n,{\mathcal {C}},d)_{q}$ angegeben, zum Teil wird diese Information in der Art der verwendeten Klammern versteckt.

Im Weiteren wird versucht, dies wie auch die Nutzung von Variablennamen sowohl in diesem Artikel wie auch in verwandten Artikeln konsistent zu halten.

Man bezeichnet allgemein ${\mathcal {C}}$ als einen $(n,{\mathcal {C}};d,q)$ -Code, falls

$\Sigma$ ein Alphabet mit $|\Sigma |=q$ ist,
der Code ${\mathcal {C}}\subseteq \Sigma ^{n}$ ist und
der (minimalen) Hamming-Abstand $d=\Delta ({\mathcal {C}})$ ist.

Betrachtet man lineare Codes, so spricht man von $[n,k;d,q]$ -Codes bzw. $[n,k;d]_{q}$ -Codes, wobei hier die Dimension von ${\mathcal {C}}$ über dem Körper $\mathbb {F} _{q}$ ist. und haben dabei die gleiche Bedeutung wie bei den allgemeinen Blockcodes.

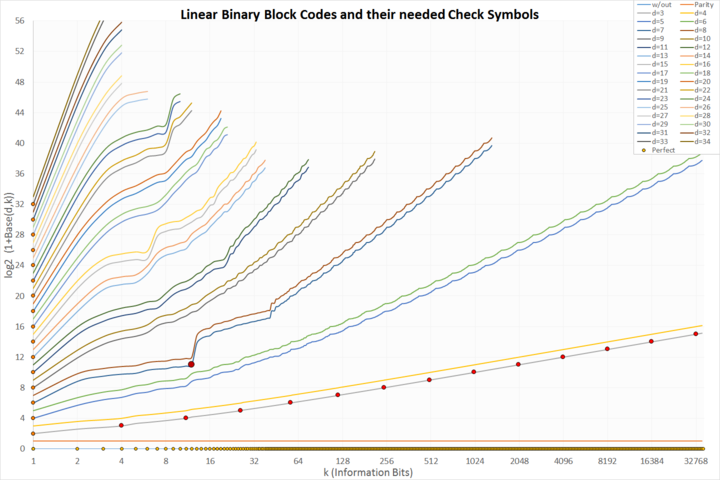
Es gibt zwar theoretische Grenzen (wie die Hamming-Grenze), aber eine andere Frage ist, welche Codes tatsächlich konstruiert werden können. Es ist, als würde man Kugeln in einem eckigen Karton verpacken … Dieses Diagramm zeigt die konstruierbaren Codes die linear und binär sind. Die x-Achse zeigt die Anzahl der geschützten Symbole k und die y-Achse die Anzahl der benötigten Prüfsymbole n-k. Es sind die Grenzen für verschiedene Hamming-Distanzen dargestellt: Von 1 (ungeschützt) bis 34.
Mit Punkten markiert sind perfekte Codes:

hellorange auf der x-Achse: trivial ungeschützte Codes
orange, auf der y-Achse: trivial Wiederholungs-Codes
dunkelorange, auf der Linie für d=3: klassische, perfekte Hamming-Codes
dunkelrot und groß: der einzige perfekte binäre Golay-Code

Man interessiert sich bei gegebenem , und für eine Maximierung der Mächtigkeit des Codes, d.h. für $\max\{|{\mathcal {C}}|:{\mathcal {C}}\,\,{\mathrm {mit} }\,\,\Delta ({\mathcal {C}})\geq d\}$ , da hierbei eine optimale Informationsrate für diese Parameter erzielt wird. Allerdings gibt es günstige Parameter, die zu effizienteren Codes als ihre Nachbarparameter führen. So fordert ein $[23,12;7,2]$ -Code 11 Schutzbits, ein $[27,13;7,2]$ -Code allerdings schon 14. Ein $[41,24;7,2]$ - kommt wie ein $[55,38;7,2]$ -Code mit 17 Schutzbits aus.

Es gibt Abschätzungen, ob Codes möglich sein könnten oder gegen gewisse Prinzipien verstoßen:

Singleton-Schranke (MDS-Code)
Hamming-Schranke (Perfekter Code)
Plotkin-Schranke
Gilbert-Varshamov-Schranke, Johnson-Schranke, Griesmer-Schranke, Bassalygo-Elias-Schranke
Optimaler Code

Schranken weisen darauf hin, ob Codes existieren können, nicht ob sie konstruierbar sind und wirklich existieren.

Typen von Blockcodes

Formal heißt der Code ${\mathcal {C}}\subseteq \Sigma ^{n}$ Blockcode, wobei $\Sigma$ als Alphabet bezeichnet wird und die Länge jedes Codewortes $c \in \mathcal C$ ist.

Triviale Blockcodes sind Codes

die nur ein Wort als Code umfassen: $|{\mathcal {C}}|=1$ . Es lassen sich alle Übertragungsfehler erkennen, aber keine Information übertragen oder
die alle möglichen Worte als Code umfassen: $|{\mathcal {C}}|=|\Sigma |^{n}$ . Es lassen sich keine Übertragungsfehler erkennen, die übertragene Information ist aber maximal.

Bemerkungen:

Der erste Code lässt sich als $[n,0;2n+1,q]$ -Code schreiben. Er hat im klassischen Sinne keine Hamming-Distanz, da es keine Codepaare gibt. Es lassen sich bis zu maximal $t=n$ Symbolfehler im übertragenen Wort korrigieren (das übertragene Codewort ist bekannt), was eine typische Eigenschaft für Codes mit $d=2t+1=2n+1$ ist. Das gleiche gilt für die Anzahl von Codes, die sich eindeutig dekodieren lassen. Die Gleichung $q^{n}={\sum _{i=0}^{\lfloor (d-1)/2\rfloor }(q-1)^{i}{\binom {n}{i}}}$ liefert für $d\geq 2n+1$ das richtige Ergebnis.
Der zweite Code lässt sich als $[n,n;1,2]$ -Code schreiben. Er hat eine Hamming-Distanz von 1.

Lineare Blockcodes sind Codes,
wenn ${\mathcal {C}}$ ein -dimensionaler Untervektorraum von $\Sigma ^{n}$ ist. Es existiert dann eine Basis $g_1, \dots, g_k$ von ${\mathcal {C}}$ . Fasst man diese Basis zu einer Matrix

$G={\begin{pmatrix}g_{1}\\g_{2}\\\vdots \\g_{k-1}\\g_{k}\end{pmatrix}}$

zusammen, erhält man eine Generatormatrix dieses linearen Blockcodes. Die Codeworte erhält man durch Multiplizieren des Eingangssignals mit der Generatormatrix

$c(x)=x\cdot G$

Der Hauptvorteil linearer Code ist die einfache Codierbarkeit und die einfache Decodierbarkeit.

Bemerkungen:

Zur Kodierung eines Codes mit $q^{k}$ Codeworten muss man nur noch Codeworte vorrätig halten. Gleiches gilt für die Dekodierung mit q^n vs. .

Systematische Blockcodes sind Codes,
bei denen die Informationssymbole direkt im Block ablesbar sind (meist am Blockanfang, siehe Abbildung am Anfang des Artikels). Sie können gleichzeitig lineare Blockcodes sein, müssen es aber nicht. Sie sind lineare Blockcodes, wenn neben den Informationssymbolen (die immer linear sind) auch die Prüfsymbole linear sind.

Perfekte Blockcodes sind Codes,
in denen jedes Wort $w\in \Sigma ^{n}$ nur zu genau einem Codewort $c \in \mathcal C$ (und nicht zu mehreren) einen geringsten Hamming-Abstand $d_{w}$ hat. Jedes Wort lässt sich damit eindeutig decodieren. Der Hamming-Code ist ein Beispiel für einen perfekten Code.

Maximum-Distanz-Codes (MDS Codes) sind Blockcodes,

deren Codeworte den größtmöglichen Hamming-Abstand voneinander haben. Beispiele für MDS Codes sind Wiederholungscodes, Paritätscodes und Reed-Solomon-Codes.

Informationsrate von Blockcodes

Die Informationsrate (auch Coderate) gibt an, wie viel Information pro Codewortsymbol im Mittel übertragen wird, sie ist also das Verhältnis von Nachrichtensymbolen zu Codewortsymbolen. Da ein Code Redundanz hinzufügt, gilt allgemein $0\leq R\leq 1$ .

Sei ${\mathcal {C}}\subseteq \Sigma ^{n}$ ein Blockcode und es gelte $q=|\Sigma |$ , das Alphabet habe also verschiedene Elemente. Dann lautet für ${\mathcal {C}}$ die Definition der Informationsrate:

$R={\frac {\log _{q}(|{\mathcal {C}}|)}{\log _{q}(|\Sigma |^{n})}}={\frac {\log _{q}(|{\mathcal {C}}|)}{n}}$ .

Ist z.B. ${\mathcal {C}}$ ein binärer Code mit verschiedenen Codeworten, dann benötigt man $\lceil \log _{2}s\rceil$ Bits, um diese eindeutig zu unterscheiden.

Handelt es sich um einen linearen Code, so ist die Informationsrate:

$R={\frac {\log _{q}(q^{k})}{n}}={\frac {k}{n}}$ .

Beispiele für Blockcodes

Wiederholungscode

Wiederholungscodes sind lineare, systematische $[n,1;n]$ -Blockcodes über einem beliebigen Alphabet, bei denen jedes Nachrichtensymbol n-mal wiederholt wird. Damit hat ein Wiederholungscode die Generatormatrix

$G={\begin{pmatrix}1\cdots 1\end{pmatrix}}$

und eine Informationsrate von $R={\frac {1}{n}}$ .

Paritätscode

Paritätscodes (engl. Single Parity Check (SPC) codes) sind lineare, systematische und binäre Codes, bei denen der Nachricht ein einziges Prüfbit angefügt wird, das sich als XOR-Verknüpfung aller Nachrichtenbits ergibt. Somit hat jedes Codewort eine gerade Anzahl an „1“-Bits. Die Generatormatrix hat folgende Form:

$G={\begin{pmatrix}10\dots 00\,\,1\\01\dots 00\,\,1\\\,\,\,\,\vdots \ddots \vdots \,\,\,\,\,\,\vdots \\00\dots 10\,\,1\\00\dots 01\,\,1\\\end{pmatrix}}$

Sie haben eine Hamming-Distanz von 2 und stellen - $[n,n-1;2,2]$ Blockcodes dar. Sie können einen Fehler erkennen, aber keine Fehler korrigieren. Lineare binäre Blockcodes mit ungeradem Hamming-Abstand $[n,k;2m+1,2]$ lassen sich mit einem zusätzlichen Paritätscode zu einem $[n+1,k;2m+2,2]$ -Code erweitern.

Hadamard-Code

Hadamard Codes sind lineare nicht-systematische Blockcodes $[2^{k},k+1;2^{k-1}]$ . Die Generatormatrix hat eine sehr auffällige Form

$G={\begin{pmatrix}01010101\cdots 10\cdots 01010101\\00110011\cdots 10\cdots 00110011\\00001111\cdots 10\cdots 00001111\\\vdots \\00000000\cdots 01\cdots 11111111\\11111111\cdots 10\cdots 00000000\\\end{pmatrix}}$

Sie haben eine geringe Coderate von $R={\frac {k+1}{2^{k}}}$ , können aber noch Daten aus sehr fehlerbehafteten Signal dekodieren. Daher fanden sie unter anderem in der Mariner 9 Mission Anwendung.

Weitere Beispiele für Blockcodes

Beispiel 1

$(9,\{0,31,227,364,437,474\};5,2)$

Die lauten in der Binärdarstellung:

.........
....#####
.###...##
#.##.##..
##.##.#.#
###.##.#.

Es existiert kein linearer Code dieser Mächtigkeit. Zum einen ist ${\text{log}}_{q}6\not \in \mathbb {N} ^{+}$ , zum anderen sind die größten lineare Code dieser Art ein $[8,2;5,2]$ - und ein $[10,3;5,2]$ -Code. Der Code lässt sich nicht in einen linearen Code umwandeln.

Beispiel 2

$(11,\{0,143,307,444,597,730,870,1001,1130,1253,1369,1494,1599,1712,1804,1923\};5,2)$

Die $|{\mathcal {C}}|=16$ Codeworte lauten in der Binärdarstellung (MSB links):

...........
...#...####
..#..##..##
..##.####..
.#..#.#.#.#
.#.##.##.#.
.##.##..##.
.#####.#..#
#...##.#.#.
#..###..#.#
#.#.#.##..#
#.###.#.##.
##...######
##.#.##....
###....##..
####.....##

Es handelt sich um einen linearen systematischen Code mit der Basis

...#...####
..#..##..##
.#..#.#.#.#
#...##.#.#.

Die 16 Codeworte lassen sich durch eine XOR-Verknüpfung der Basisvektoren erzeugen, deren Informationsbits gesetzt sind (daher linearer Code). Die Informationsbits stellen die linken 4 Bit dar (Bit 10 bis 7), die Schutzbits die rechten 7 Bit (Bit 6 bis 0) (daher systematischer Code).

Beispiel 3

$(8,\{0,7,25,30,42,53,75,84,97,108,114,127,140,147,166,169,176,194,197,216\};3,2)$

Die $|{\mathcal {C}}|=20$ Codeworte lauten in der Binärdarstellung:

........
.....###
...##..#
...####.
..#.#.#.
..##.#.#
.#..#.##
.#.#.#..
.##....#
.##.##..
.###..#.
.#######
#...##..
#..#..##
#.#..##.
#.#.#..#
#.##....
##....#.
##...#.#
##.##...

Es existiert kein linearer Code dieser Mächtigkeit. Auch hier ist zum einen ${\text{log}}_{q}20\not \in \mathbb {N} ^{+}$ , zum anderen sind die größten lineare Code dieser Art ein $[7,4;3,2]$ - und ein $[9,5;3,2]$ -Code. Der Code lässt sich nicht in einen linearen Code umwandeln.

Fehlerkorrektur

Blockcodes können zur Fehlererkennung und Fehlerkorrektur bei der Übertragung von Daten über fehlerbehaftete Kanäle verwendet werden. Dabei ordnet der Sender dem zu übertragenen Informationswort der Länge ein Codewort der Länge zu, wobei $n>k$ . Durch das Hinzufügen der n-k zusätzlichen Symbole entsteht Redundanz und die Informationsrate sinkt; jedoch kann der Empfänger die redundante Information nun dazu nutzen Übertragungsfehler zu erkennen und zu korrigieren.

Verwendet man beispielsweise, im Fall der Binärkodierung, die Zuordnung

Informationswort	Codewort
0	000
1	111

so können empfangene Codewörter mit genau einem Bitfehler korrigiert werden, indem man mit Hilfe einer Mehrheitsfunktion das abweichende Bit umkehrt:

Fehlerhaftes Codewort	Korrigiertes Codewort	Zugeordnetes Informationswort
001	000	0
010	000	0
011	111	1
100	000	0
101	111	1
110	111	1

Sind in diesem Falle jedoch zwei Bits falsch, so wird zwar ein Fehler erkannt, aber fehlerhaft korrigiert. Sind gar drei Bits falsch, so kann nicht einmal mehr ein Fehler erkannt werden.

Schranken

Singleton-Schranke

Die Singleton-Schranke bezeichnet eine obere Schranke für die Mindestdistanz eines Blockcodes der Länge bei Informationswörtern der Länge über einem einheitlichen Alphabet $\Sigma$ .

Sie lautet:

$d\leq n-k+1$

Die Schranke kann auf folgende Art intuitiv klargemacht werden:

Annahme: Alphabet $\Sigma =\{0,\ldots ,q-1\}$
Anzahl der möglichen Informationswörter: $|{\mathcal {I}}|=q^{k}$
Anzahl der Codewörter: $|{\mathcal {C}}|=|{\mathcal {I}}|=q^{k}$
Mindestdistanz:

Streicht man nun in den Codewörtern jeweils die letzten ( d-1 ) der Stellen, so haben die übrigen Codewörter zueinander immer noch mindestens den Hamming-Abstand 1. Bei Streichungen wäre dies nicht mehr gewährleistet. Damit sind immer noch alle Codewörter unterschiedlich, also

$|{\mathcal {C}}'|=|{\mathcal {C}}|=q^{k}$

Deswegen muss auch die Anzahl der durch die Länge $n-(d-1)$ erzeugbaren Wörter $q^{n-d+1}\geq q^{k}$ sein. Stellt man diese Gleichung um, ergibt sich daraus die Singleton-Schranke

$n-d+1\geq k\Leftrightarrow d\leq n-k+1$

Für nicht-lineare Codes gilt entsprechend

$M\leq q^{n-d+1}$ ,

wobei $M=|{\mathcal {C}}|$ .

Codes, die die Singleton-Schranke mit Gleichheit erfüllen, nennt man auch MDS-Codes.

Im Falle der Hamming-Schranke ist $t=\lfloor (d-1)/2\rfloor$ die Anzahl der maximal korrigierbaren Fehler eines Codes mit der Hamming-Distanz .

Die Hamming-Schranke sagt aus, dass

$q^{n}\geq q^{k}{\sum _{i=0}^{t}(q-1)^{i}{\binom {n}{i}}}$ ,

beziehungsweise

$n\geq k+\log _{q}{\sum _{i=0}^{t}(q-1)^{i}{\binom {n}{i}}}$

erfüllt sein muss für einen Code, der mittels Symbolen eines Alphabets $\Sigma$ der Größe eine Nachricht mit der Länge transportiert.

Die Singleton-Schranke ist eine ungenauere Abschätzung als die Hamming-Schranke, die die Größe des Alphabets nicht berücksichtigt. Weiterhin gibt es Unterschiede in der Beziehung zwischen und .

Plotkin-Grenze

In der Kanalcodierung verwendet man Blockcodes, um Fehler in Datenströmen erkennen und korrigieren zu können. Ein Blockcode der Länge über einem -nären Alphabet mit einem Minimalabstand erfüllt die Plotkin-Grenze, auch als Plotkin-Schranke bezeichnet,

$|C|\leq {\frac {d}{d-({\frac {q-1}{q}})\cdot n}}$

dann, wenn der Nenner positiv ist. Somit liefert die Plotkin-Grenze nur dann ein Resultat, wenn hinreichend nahe bei liegt.

Nimmt ein Code die Plotkin-Schranke an, so gilt insbesondere, dass der Abstand zweier beliebiger Codewörter genau ist.

Ist $q\geq 3$ und $|C|=a\cdot q+b$ mit $b<q$ , so gilt sogar die schärfere Beziehung:

$d{|C| \choose 2}\leq n\left({|C| \choose 2}-b{a+1 \choose 2}-(q-b){a \choose 2}\right)$

Beispielsweise liefert die Plotkin-Grenze für q=3 , n=9 und $d=7$ nur $|C|\leq 7$ , die Verschärfung jedoch $|C|\leq 6$ , da sich für a=2 und b=1 ein Widerspruch ergibt.

Sie wurde 1960 von Morris Plotkin veröffentlicht.

Literatur

Rudolf Nocker: Digitale Kommunikationssysteme 1. Grundlagen der Basisbandübertragung, 1. Auflage, Friedrich Vieweg & Sohn Verlag, Wiesbaden 2004, ISBN 978-3-528-03976-9.
Markus Hufschmid: Information und Kommunikation. Grundlagen der Informationsübertragung, Vieweg und Teubner, Wiesbaden 2006, ISBN 3-8351-0122-6.
Bernd Friedrichs: Kanalcodierung. Grundlagen und Anwendungen in modernen Kommunikationssystemen. Springer Verlag, Berlin/ Heidelberg 1995, ISBN 3-540-59353-5.

Basierend auf einem Artikel in:

Wikipedia.de