Bahnachse

Keplerbahnen und Bahnachsen

Bahnachsen sind in der Astronomie die Symmetrieachsen von geschlossenen elliptischen Umlaufbahnen (Keplerbahnen). Die große Halbachse ist die Entfernung der Hauptscheitel vom Mittelpunkt der Ellipse und damit die größte Strecke, die sich vom Mittelpunkt aus in einer Ellipse legen lässt.

Bedeutung für die Bahnberechnung

Nach dem ersten Keplerschen Gesetz läuft ein Himmelskörper nicht um den Mittelpunkt der Ellipse (auf halbe Länge zwischen den Scheiteln), sondern um einen der beiden Brennpunkte. Daher wird seine Bahn im Allgemeinen in einem Koordinatensystem beschrieben, dessen Ursprung im Brennpunkt mit dem Massezentrum liegt (Bahnkoordinatensystem). Der Abstand zum Ursprung wird dann durch den Radiusvektor beschrieben.

Wie sehr sich auf der Umlaufbahn der Abstand des umlaufenden Körpers vom Koordinatenursprung verändert, hängt in erster Linie von der Exzentrizität^[1] der Bahnellipse ab:

der minimale Abstand errechnet sich aus großer Halbachse minus linearer Exzentrizität, $a-r_{\mathrm {min} }$ ,
der Maximalwert aus $a+r_{\mathrm {min} }$ .

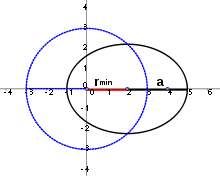
Mit abnehmender Exzentrizität bei unveränderter Halbachse nähern sich der Ellipsenmittelpunkt, in der Zeichnung bei (2|0), und der zweite Brennpunkt, in der Zeichnung bei (4|0), immer weiter dem ersten Brennpunkt (0|0) an. Im Grenzfall $r_{\mathrm {min} }=0$ ergibt sich als Bahn ein Kreis, der die gleiche Bahnachse bzw. Radius hat wie die dargestellte Ellipse (nämlich 3 Längeneinheiten). Auf diesen beiden verwandten Bahnen umkreist ein kleiner Körper eine große Masse im Brennpunkt bei (0|0) nach dem dritten Keplerschen Gesetz mit der gleichen Umlaufzeit.

Einfluss des Baryzentrums

Die keplersche Planetentheorie ist eine Idealisierung, die die Gravitation des kleineren auf den größeren Körper vernachlässigt. In der Realität umkreisen beide einen gemeinsamen Schwerpunkt, in der Himmelsmechanik das Baryzentrum des Systems genannt.

Beispiel der Mondbahn (durchschnittlich):
erdnächster Punkt (Perigäum)	362.102 km
erdfernster Punkt (Apogäum)	404.694 km
Mittelwert (Große Halbachse)	383.398 km
Große Halbachse der Mondbahn	378.739 km
Große Halbachse der Erdbahn	004.659 km

Die letzten beiden Werte beziehen sich auf die Bewegung von Erde und Mond um den Erde-Mond-Schwerpunkt (EMS). Da der Mond etwa 1/81 der Erdmasse besitzt, liegt der EMS durchschnittlich 4700 km vom Erdzentrum entfernt (Bahnachse der Erde um den EMS), also etwa 1700 km unterhalb der Erdoberfläche. Ist der Mond erdfern, so liegt der EMS weiter vom Erdmittelpunkt entfernt, ist der Mond dagegen erdnah, so ist auch der Abstand Erdmittelpunkt–EMS geringer. Diese Schwankung bleibt unter ein paar hundert Kilometern.

Bei den Monden anderer Planeten tritt dieser Unterschied kaum in Erscheinung, da ihre relativen Massen viel geringer sind. Hier kann man als Bahnachse den Mittelwert der beiden Extremwerte nehmen, von denen schon Kepler als „mittlere Entfernung“ sprach.

Auch bei den Planetenbahnen ist der baryzentrische Unterschied minimal – mit Ausnahme der „Riesenplaneten“ Jupiter und Saturn, die etwa 1,0 ‰ und 0,3 ‰ der Sonnenmasse besitzen.

Anmerkungen

↑ In der Mathematik bezeichnet $\epsilon$ die numerische Exzentrizität, in der Astronomie wird sie als angegeben, sie liegt im Intervall . Die lineare Exzentrizität, mathematisch , ein Längenmaß, z.B. in Kilometern oder Astronomischen Einheiten, bezeichnet den Abstand $r_\mathrm{min}$ zwischen Brennpunkt und Mittelpunkt der Ellipse.

Basierend auf einem Artikel in:

Wikipedia.de