Simpliziale Homologie

Die Simpliziale Homologie ist in der Algebraischen Topologie, einem Teilgebiet der Mathematik, eine Methode, die einem beliebigen Simplizialkomplex eine Folge abelscher Gruppen zuordnet. Anschaulich gesprochen zählt sie die Löcher unterschiedlicher Dimension des zugrunde liegenden Raumes.

Simplizialkomplexe

Ein simplizialer Komplex ist eine Menge von (durch ihre Eckpunkte eindeutig bestimmten) Simplizes, so dass jede Seitenfläche eines der Simplizes wieder in dieser Menge liegt. Einfache Beispiele sind Polygone und Polyeder. Nach einem Satz der Topologie kann man jede differenzierbare Mannigfaltigkeit triangulieren, also als einen simplizialen Komplex (SK) auffassen.

Simpliziale Homologie

Zu einem Simplizialkomplex betrachten wir für $n=0,1,2,\ldots$ die freie abelsche Gruppe über der Menge der -Simplizes des simplizialen Komplexes $C_{n}(K)$ .

Elemente von $C_{n}(K)$ sind also formale Summen der Form

$\sum _{i=1}^{r}a_{i}\sigma _{i}$

mit $a_{i}\in \mathbb{Z }$ und $\sigma _{i}$ ein -Simplex von . Dabei wird gefordert, dass $\sigma _{i}=-\sigma _{j}$ gilt, wenn die Simplizes $\sigma _{i}$ und $\sigma _{j}$ umgekehrte Orientierung besitzen.

Die "Randabbildung" $\partial \colon C_{n}(K)\rightarrow C_{n-1}(K)$ bilde jeden Simplex auf die alternierende Summe seiner Seitenflächen ab, das heißt

$\partial ([v_{0},\dots ,v_{n}]):=\sum _{i=0}^{n}(-1)^{i}[v_{0},\ldots ,{\hat {v_{i}}},\ldots ,v_{n}]\,,$

wobei ${\hat {v}}_{i}$ bedeutet, dass $v_{i}$ ausgelassen wird. Die alternierenden Vorzeichenfaktoren können auch als „geometrische Orientierungszahlen“ interpretiert werden.

Diese auf den Erzeugern von $C_{n}(K)$ definierte Randabbildung setzt sich durch lineare Fortsetzung

$\partial (\sum _{i=1}^{r}a_{i}\sigma _{i})=\sum _{i=1}^{r}a_{i}\partial (\sigma _{i})$

eindeutig zu einer Abbildung $\partial :C_{n}(K)\rightarrow C_{n-1}(K)$ fort. Man rechnet leicht nach, dass

$\partial \circ \partial =0$

gilt. $(C_{*}(K),\partial )$ ist also ein Kettenkomplex.

Die Homologie dieses Kettenkomplexes heißt die simpliziale Homologie von und wird mit $H_{*}(K)$ bezeichnet.

Beispiel

Rechenbeispiel

Dreieck

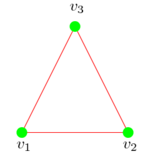
Wir wollen die Homologiegruppen des Dreiecks (bestehend aus drei 0-Simplizes $v_{1},v_{2},v_{3}$ und den drei sie verbindenden 1-Simplizes, keinem 2-Simplex und keinen höherdimensionalen Simplizes) berechnen.

Nach Definition des Randoperators ist $\partial _{0}([v_{i}])=0$ , also:

$\mathrm {ker} (\partial _{0})=C_{0}=\{a_{1}[v_{1}]+a_{2}[v_{2}]+a_{3}[v_{3}]|a_{1},a_{2},a_{3}\in \mathbb {Z} \}\cong \mathbb {Z} \oplus \mathbb {Z} \oplus \mathbb {Z}$

d.h. alle 0-Ketten sind im Kern.

Für eine 1-Kette $c_{1}=b_{1}[v_{1},v_{2}]+b_{2}[v_{2},v_{3}]+b_{3}[v_{3},v_{1}]$ ist

$\partial _{1}(c_{1})=(b_{3}-b_{1})[v_{1}]+(b_{1}-b_{2})[v_{2}]+(b_{2}-b_{3})[v_{3}]$

Daraus erhält man

$\mathrm {Im} (\partial _{1})=\{(b_{3}-b_{1})[v_{1}]+(b_{1}-b_{2})[v_{2}]+(b_{2}-b_{3})[v_{3}]|b_{1},b_{2},b_{3}\in \mathbb {Z} \}$ ,

eine 0-Kette $c_{0}=a_{1}[v_{1}]+a_{2}[v_{2}]+a_{3}[v_{3}]$ gehört also genau dann zum Bild von $\partial _{1}$ , wenn

$a_{1}=b_{3}-b_{1}$

$a_{2}=b_{1}-b_{2}$

$a_{3}=b_{2}-b_{3}$ ,

also genau dann, wenn $a_{1}+a_{2}+a_{3}=0$ . Daraus folgt

$H_{0}(S)\cong (\mathbb {Z} \oplus \mathbb {Z} \oplus \mathbb {Z} )/(a_{1}+a_{2}+a_{3}=0)\cong \mathbb {Z}$

Zur Berechnung der ersten Homologiegruppe: Für eine 1-Kette

$c_{1}=b_{1}[v_{1},v_{2}]+b_{2}[v_{2},v_{3}]+b_{3}[v_{3},v_{1}]$

ist $\partial _{1}(c_{1})=0$ genau dann, wenn $b_{1}=b_{2}=b_{3}$ , also

$\mathrm {ker} (\partial _{1})=\{b[v_{1},v_{2}]+b[v_{2},v_{3}]+b[v_{3},v_{1}]|b\in \mathbb {Z} \}\cong \mathbb {Z} .$

Weil es keine 2-Simplizes gibt, sind Kern und Bild von $\partial _{2}$ trivial, $\mathrm {ker} (\partial _{2})=\mathrm {Im} (\partial _{2})=0$ . Damit erhalten wir:

$H_{1}(S)=\mathrm {ker} (\partial _{1})/\mathrm {Im} (\partial _{2})=\mathrm {ker} (\partial _{1})\cong \mathbb {Z}$

$H_{2}(S)=\mathrm {ker} (\partial _{2})/\mathrm {Im} (\partial _{3})\cong 0$

und trivialerweise $H_{i}(S)\cong 0$ für alle $i>2$ .

Weitere Beispiele

Es gelten:

Ist der simpliziale Komplex, der das Dreieck mit Inhalt trianguliert. Das heißt der Komplex wie oben, nur zusätzlich mit dem 2-Simplex. Dann ergibt sich $H_{0}(K)=\mathbb {Z} ,\,H_{1}(K)=H_{2}(K)=\ldots =0$
Für den 2-Torus $T=S^{1}\times S^{1}$ gilt $H_{1}(T)=\mathbb {Z} ^{2},\,H_{2}(T)=\mathbb {Z}$ und $H_{i}(T)=0$ für $i>2$ .
Für die Kleinsche Flasche gilt $H_{1}(K)=\mathbb {Z} \oplus \mathbb {Z} /2\mathbb {Z}$ und $H_{i}(K)=0$ für $i\geq 2$ .
Es gilt $H_{1}(\mathbb {R} P^{2})=\mathbb {Z}$ und $H_{i}(\mathbb {R} P^{2})=0$ für alle $i\geq 2$ .
Sei ein simplizialer Komplex mit $n\in \mathbb {N}$ Zusammenhangskomponenten, dann gilt $H_{0}(K)=\mathbb {Z} ^{n}$ .

Funktorialität

Simpliziale Abbildungen

Eine simpliziale Abbildung $f\colon K\to L$ induziert eine Kettenabbildung

$f_{*}:C_{*}(K)\rightarrow C_{*}(L)$

durch

$f_{*}(\sum _{i=1}^{r}a_{i}\sigma _{i})=\sum _{i=1}^{r}a_{i}f(\sigma _{i})$

und wegen $df=fd$ eine wohldefinierte Abbildung

$f_{*}:H_{*}(K)\rightarrow H_{*}(L)$ .

Stetige Abbildungen

Sei

$f:\vert K\vert \to \vert L\vert$

eine stetige Abbildung zwischen den Geometrischen Realisierungen zweier Simplizialkomplexe und . Wir bezeichnen mit $Bd(K)$ die baryzentrische Unterteilung von und mit $Bd^{n}(K)$ die -fach iterierte baryzentrische Unterteilung. Es gilt $\vert Bd^{n}(K)\vert =\vert K\vert$ .

Nach dem simplizialen Approximationssatz gibt es ein $n\in \mathbb {N}$ , so dass $f:\vert Bd^{n}(K)\vert \to \vert L\vert$ eine simpliziale Approximation

$g:Bd^{n}(K)\rightarrow L$

besitzt.

Dann wird

$f_{*}:H_{*}(K)\rightarrow H_{*}(L)$

definiert als die Verknüpfung von $g_{*}$ mit dem kanonischen Isomorphismus $H_{*}(K)\to H_{*}(Bd^{n}(K))$ . Man kann zeigen, dass der so definierte Homomorphismus $f_{*}$ unabhängig von der Wahl der simplizialen Approximation ist.

Simpliziale Homologie mit Koeffizienten

Für eine abelsche Gruppe und einen Simplizialkomplex definiert man

$C_{*}(K,G)=C_{*}(K)\otimes _{\mathbb {Z} }G$ ,

Elemente von $C_{n}(K,G)$ sind also formale Summen der Form $\textstyle \sum _{i=1}^{r}a_{i}\sigma _{i}$ mit $a_{i}\in G$ und $\sigma _{i}$ ein -Simplex in . Der Randoperator setzt sich fort mittels

$d(\sum _{i=1}^{r}a_{i}\sigma _{i})=\sum _{i=1}^{r}a_{i}d\sigma _{i}$ .

Die Homologie mit Koeffizienten in G

$H_{*}(X,G)$

ist definiert als die Homologie des Kettenkomplexes $(C_{*}(X,G),d)$ .

Simpliziale versus Singuläre Homologie

Die simpliziale Homologie eines Simplizialkomplexes ist isomorph zur singulären Homologie seiner geometrischen Realisierung:

$H_{*}(K,G)=H_{*}(\vert K\vert ,G)$ .

Basierend auf einem Artikel in:

Wikipedia.de