Fixpunktfreie Permutation

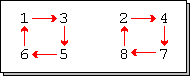
Graph einer fixpunktfreien Permutation der Zahlen von 1 bis 8. Durch die Permutation wird keine der Zahlen festgehalten.

Eine fixpunktfreie Permutation oder Derangement (von französisch déranger „durcheinanderbringen“) ist in der Kombinatorik eine Permutation der Elemente einer Menge, sodass kein Element seine Ausgangsposition beibehält. Die Anzahl möglicher fixpunktfreier Permutationen einer Menge mit Elementen wird durch die Subfakultät {!}n angegeben. Für wachsendes strebt innerhalb der Menge der Permutationen von Elementen der Anteil der fixpunktfreien Permutationen sehr schnell gegen den Kehrwert der eulerschen Zahl . Sollen in einer Permutation manche der Elemente an ihrem alten Platz verbleiben, spricht man von einem partiellen Derangement, deren Anzahl durch die Rencontres-Zahlen ermittelt werden kann.

Ausgangsproblem

Beim Treize-Spiel gewinnt der Spieler, wenn bei 13 durchmischten Spielkarten einer Farbe (untere Reihe) mindestens eine Karte in der richtigen Reihenfolge (obere Reihe) auftritt, hier die Zehn.

Der französische Mathematiker Pierre Rémond de Montmort stellte Anfang des 18. Jahrhunderts in seinem Buch Essai d’analyse sur les jeux de hazard ein Spiel namens Treize („Dreizehn“) vor, das in vereinfachter Form wie folgt beschrieben werden kann:

Ein Spieler mischt einen Satz von 13 Spielkarten einer Farbe und legt ihn als Stapel vor sich hin. Nun deckt er die Karten der Reihe nach auf, wobei er jede Karte gemäß der Reihenfolge As, Zwei, Drei bis König aufruft. Sollte irgendwann die aufgerufene Karte mit der aufgedeckten Karte übereinstimmen, so gewinnt er das Spiel; trifft dies bei keiner der 13 Karten zu, verliert er.

Nun stellt de Montmort sich die Frage nach der Wahrscheinlichkeit, mit der der Spieler das Spiel gewinnt. In der ersten Auflage seines Buchs von 1708 gibt de Montmort zwar das korrekte Ergebnis an, allerdings ohne genauere Herleitung. In der zweiten Auflage von 1713 stellt er dann zwei Beweise vor, einen eigenen, der auf einer rekursiven Darstellung beruht, und einen weiteren aus einem Briefwechsel mit Nikolaus I Bernoulli, der auf dem Inklusions-Exklusions-Prinzip basiert. De Montmort zeigt weiter, dass die Gewinnwahrscheinlichkeit sehr nahe an dem Wert von $1-e^{{-1}}\approx 0{,}6321$ liegt. Vermutlich stellt dies die erste Verwendung der Exponentialfunktion in der Wahrscheinlichkeitstheorie dar.

Ohne die Vorarbeiten zu kennen, analysierte Leonhard Euler 1753 ein verwandtes Glücksspiel namens Rencontre („Wiederkehr“), das folgendermaßen abläuft:

Zwei Spieler besitzen jeweils ein vollständiges Kartenspiel mit 52 Karten. Sie mischen ihre Karten und legen diese als Stapel vor sich ab. Nun ziehen beide Spieler gleichzeitig immer wieder die oberste Karte von ihrem Stapel. Erscheint zu irgendeinem Zeitpunkt zweimal die gleiche Karte, so gewinnt der eine Spieler, andernfalls der andere.

Wiederum stellt sich die Frage nach der Gewinnwahrscheinlichkeit. Euler leitet die Lösung mit Hilfe weiterer Rekurrenzformeln her, wobei er annehmen darf, dass nur einer der Spieler seine Karten mischt und der andere Spieler seine Karten in einer vorgegebenen Reihenfolge aufdeckt. Weitere Varianten und Verallgemeinerungen der Fragestellung wurden unter anderem von de Moivre, Lambert und Laplace untersucht.

In modernen Lehrbüchern zur Kombinatorik wird das Problem häufig als „Problem der vertauschten Hüte“ (auch Mäntel, Koffer, Briefe oder ähnliches) in etwa so formuliert:

Bei einem Empfang geben Gäste ihre Hüte an der Garderobe ab. Die Garderobenfrau ist an diesem Abend jedoch sehr zerstreut und gibt beim Verlassen jedem Gast einen zufällig gewählten Hut zurück. Wie groß ist die Wahrscheinlichkeit, dass mindestens ein Gast den richtigen Hut erhält?

Die drei mathematischen Probleme sind zueinander äquivalent und können durch das Studium fixpunktfreier Permutationen gelöst werden.

Definition

Ist $S_{n}$ die symmetrische Gruppe aller Permutationen der Menge $\{1,\ldots ,n\}$ , dann heißt eine Permutation $\pi = ( \pi(1), \pi(2), \ldots , \pi(n) ) \in S_n$ fixpunktfrei, wenn

$\pi(i) \neq i$

für alle $i=1,\ldots ,n$ gilt. Eine fixpunktfreie Permutation ist damit eine Permutation, bei der kein Element seine Ausgangsposition beibehält, das heißt, es tritt kein Zyklus der Länge eins auf. Bezeichnet $D_{n}$ die Menge aller fixpunktfreien Permutationen in $S_{n}$ und $d_{n}=|D_{n}|$ deren Anzahl, dann entspricht der Anteil

$p_{n}={\frac {|D_{n}|}{|S_{n}|}}={\frac {d_{n}}{n!}}$ .

nach der Laplace-Formel gerade der Wahrscheinlichkeit für das Auftreten einer fixpunktfreien Permutation, wenn man annimmt, dass alle möglichen Permutationen in $S_{n}$ gleich wahrscheinlich sind. Allgemeiner können auch Permutationen beliebiger endlicher Mengen, beispielsweise Alphabete, betrachtet werden, zur Analyse der mathematischen Eigenschaften kann man sich jedoch auf die ersten natürlichen Zahlen beschränken.

Beispiele

Die neun fixpunktfreien Permutationen von vier Elementen sind hervorgehoben

Ein Fixpunkt einer Permutation ist dadurch charakterisiert, dass in ihrer Zweizeilenform zweimal die gleiche Zahl untereinander steht. Die einzige Permutation in $S_{1}$

$\begin{pmatrix} 1 \\ 1 \end{pmatrix}$

hat einen Fixpunkt und es gilt damit $d_{1}=0$ und $p_{1}=0$ . Die beiden Permutationen in $S_{2}$ sind

${\begin{pmatrix}1&2\\1&2\end{pmatrix}}$ und ${\begin{pmatrix}1&2\\2&1\end{pmatrix}}$ ,

wobei die erste zwei Fixpunkte hat und die zweite keinen. Es gilt also $d_{2}=1$ und $p_{2}={\tfrac 12}$ . Von den sechs Permutationen in $S_{3}$

${\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}},{\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}},{\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}},{\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}},{\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}$ und ${\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}$

sind nur die vierte und fünfte fixpunktfrei, es gilt also $d_{3}=2$ und $p_{3}={\tfrac 26}={\tfrac 13}$ .

In S_0 besteht die Trägermenge aus der leeren Menge mit der einzigen Permutation darin, die leere Menge auf die leere Menge abzubilden. Da aus der leeren Menge kein Element ausgewählt werden kann, ist diese Permutation fixpunktfrei und es gilt $d_{0}=1$ und $p_{0}=1$ .

Anzahl

	fixpunktfreie Permutationen	alle Permutationen	Anteil
0	1	1	1
1	0	1	0
2	1	2	0,5
3	2	6	0,33333333…
4	9	24	0,375
5	44	120	0,36666666…
6	265	720	0,36805555…
7	1.854	5.040	0,36785714…
8	14.833	40.320	0,36788194…
9	133.496	362.880	0,36787918…
10	1.334.961	3.628.800	0,36787946…

Die Anzahl der fixpunktfreien Permutationen in $S_{n}$ lässt sich mit Hilfe der Subfakultät durch

$d_{n}={!}n=n!\cdot \sum _{{k=0}}^{n}{\frac {(-1)^{k}}{k!}}$ (Folge

A000166 in OEIS)

ausdrücken. Der Anteil der fixpunktfreien Permutationen in $S_{n}$ ist entsprechend

$p_{n}={\frac {{!}n}{n!}}=\sum _{{k=0}}^{n}{\left(-1\right)^{k} \over k!}$ .

Die Anzahl der fixpunktfreien Permutationen $d_{n}$ und ihr Anteil an der Gesamtzahl der Permutationen $p_{n}$ sind für n=0 bis in nebenstehender Tabelle zusammengefasst.

Für $n\geq 4$ liegt damit der Anteil der fixpunktfreien Permutationen bei etwa 37 % (daher auch 37%-Regel). Asymptotisch gilt für diesen Anteil

$\lim _{{n\to \infty }}p_{n}=\sum _{{k=0}}^{\infty }{\frac {(-1)^{k}}{k!}}={\frac {1}{e}}$ ,

wobei die eulersche Zahl ist.

Herleitungen

Herleitung über das Inklusions-Exklusions-Prinzip

Nach dem Prinzip von Inklusion und Exklusion ergibt sich die Mächtigkeit der Vereinigung dreier Mengen $|A\cup B\cup C|$ aus der Summe der Mächtigkeiten der einzelnen Mengen $|A|+|B|+|C|$ minus der Summe der Mächtigkeiten der Schnittmengen von je zwei Mengen $|A\cap B|+|A\cap C|+|B\cap C|$ plus der Mächtigkeit der Schnittmenge der drei Mengen $|A\cap B\cap C|$ .

Bezeichnet

$A_{i}=\{\pi \in S_{n}\mid \pi (i)=i\}$

die Menge der Permutationen, die einen Fixpunkt an der Stelle aufweisen, dann hat die Menge der fixpunktfreien Permutationen die Darstellung

$D_{n}=S_{n}\setminus (A_{1}\cup \ldots \cup A_{n})$ .

Damit ist die Anzahl der fixpunktfreien Permutationen durch

$d_{n}=n!-|A_{1}\cup \ldots \cup A_{n}|$

gegeben. Nach dem Prinzip von Inklusion und Exklusion gilt nun für die Mächtigkeit einer Vereinigungsmenge

$|A_{1}\cup \ldots \cup A_{n}|=\sum _{{k=1}}^{n}(-1)^{{k-1}}\sum _{{1\leq i_{1}<\ldots <i_{k}\leq n}}\left|A_{{i_{{1}}}}\cap \cdots \cap A_{{i_{k}}}\right|$ .

Jede der Schnittmengen $|A_{{i_{1}}}\cap \ldots \cap A_{{i_{k}}}|$ besteht aus den Permutationen mit mindestens den Fixpunkten $i_{1},\ldots ,i_{k}$ und demnach gilt

$|A_{{i_{1}}}\cap \ldots \cap A_{{i_{k}}}|=(n-k)!$ .

Nachdem es ${\tbinom {n}{k}}$ Möglichkeiten gibt, Fixpunkte auszuwählen, erhält man so

$|A_{1}\cup \ldots \cup A_{n}|=\sum _{{k=1}}^{n}(-1)^{{k-1}}{\binom nk}(n-k)!=\sum _{{k=1}}^{n}(-1)^{{k-1}}{\frac {n!}{k!}}$

und weiter

$d_{n}=n!-\sum _{{k=1}}^{n}(-1)^{{k-1}}{\frac {n!}{k!}}=n!\cdot \sum _{{k=0}}^{n}{\frac {(-1)^{k}}{k!}}$ .

Herleitung über Rekurrenzen

${\begin{pmatrix}1&\,2\,&3&\cdots &n\\2&\;1\;&\neq \!\!3&\cdots &\neq \!\!n\end{pmatrix}}$

${\begin{pmatrix}1&2&3&\cdots &n\\2&\neq \!\!1&\neq \!\!3&\cdots &\neq \!\!n\end{pmatrix}}$

Bei der Herleitung sind zwei Fälle zu unterscheiden: ist $\pi (1)=j$ , dann kann entweder $\pi(j) = 1$ sein (oben) und es verbleiben $n-2$ Bedingungen oder es ist $\pi (j)\neq 1$ (unten), dann verbleiben n-1

Bedingungen. Im Beispiel ist j=2

Ist $\pi \in D_{n}$ mit $n\geq 3$ eine fixpunktfreie Permutation, dann gilt per Definition $\pi (1)\neq 1$ . Nun werden die folgenden zwei Fälle unterschieden:

Befindet sich die Zahl an der Stelle $j=\pi (1)$ , dann können die übrigen Zahlen auf $d_{{n-2}}$ Möglichkeiten fixpunktfrei auf die verbleibenden Plätze verteilt werden.
Ansonsten betrachtet man die Menge $\{1,\ldots ,n\}\setminus \{j\}$ . Diese Zahlen müssen nun die Positionen $2,3,\ldots ,n$ einnehmen, sodass keine der Zahlen festbleibt und zudem die nicht an der Stelle steht. Die Anzahl der Möglichkeiten dies zu erreichen ist gerade $d_{{n-1}}$ .

Nachdem es n-1 mögliche Werte für gibt, folgt daraus die lineare Rekurrenz

$d_{n}=(n-1)(d_{{n-1}}+d_{{n-2}})$

mit $d_{1}=0$ und $d_{2}=1$ . Diese Rekurrenz lässt sich nun zu

$d_{n}-nd_{{n-1}}=-(d_{{n-1}}-(n-1)d_{{n-2}})$ .

umformen. Mit der Ersetzung $b_{n}=d_{n}-nd_{{n-1}}$ erkennt man $b_{n}=-b_{{n-1}}$ , also b_n = (-1)^n , und damit

$d_{n}=nd_{{n-1}}+(-1)^{n}$ .

Die explizite Summenformel kann dann durch vollständige Induktion verifiziert werden:

$d_{n}=n!\cdot \sum _{{k=0}}^{n}{\frac {(-1)^{k}}{k!}}=n!\cdot \sum _{{k=0}}^{{n-1}}{\left(-1\right)^{k} \over k!}+n!\cdot {\frac {(-1)^{n}}{n!}}=nd_{{n-1}}+(-1)^{n}$

wobei $d_{2}=2({\tfrac 12}-{\tfrac 11}+{\tfrac 11})=2\cdot d_{1}+(-1)^{2}$ .

Partielle Derangements

Rencontres-Zahlen *d_n,k*
${}_{n}\!\diagdown \!\!{}^{k}$	0	1	2	3	4	5	Summe
0	1						1
1	0	1					1
2	1	0	1				2
3	2	3	0	1			6
4	9	8	6	0	1		24
5	44	45	20	10	0	1	120

Sollen in einer Permutation $\pi \in S_{n}$ genau Zahlen an ihrem Platz verbleiben, so spricht man von einem unvollständigen oder partiellen Derangement. So sind beispielsweise die drei partiellen Derangements in $S_{3}$ , bei der genau eine Zahl an ihrem Platz bleibt

${\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}},{\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}$ und ${\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}}$ .

Bezeichnet nun $D_{n,k}$ die Menge der partiellen Derangements in $S_{n}$ bei denen genau Zahlen an ihrem Platz verbleiben, dann wird die Anzahl $d_{{n,k}}=|D_{{n,k}}|$ durch die Rencontres-Zahlen

$d_{{n,k}}={!}(n-k){\binom nk}={\frac {n!}{k!}}\cdot \sum _{{i=0}}^{{n-k}}{\left(-1\right)^{i} \over i!}$

angegeben (Folge A008290 in OEIS). Als Spezialfall für k=0 erhält man mit $D_{n}=D_{{n,0}}$ die Menge der fixpunktfreien Permutationen und mit $d_{n}=d_{{n,0}}$ die Subfakultät.

Anwendungen

Vertauschung von Buchstaben im Walzensatz der ENIGMA

Die deutsche Schlüsselmaschine ENIGMA, die während des Zweiten Weltkriegs zum Einsatz kam, führte konstruktionsbedingt fixpunktfreie (und selbstinverse) Permutationen durch. Eine spezielle Walze, nämlich die ganz links liegende Umkehrwalze, bewirkte, dass der Strom den Walzensatz zweimal durchfloss, einmal in Hinrichtung und einmal in Rückrichtung. Dadurch konnte ein Buchstabe nicht mehr in sich selbst verschlüsselt werden, was zwar die Konstruktion und Bedienung der Maschine vereinfachte, da Verschlüsselung und Entschlüsselung hierdurch gleich waren, zugleich allerdings eine signifikante kryptographische Schwächung bewirkte.

Das Wichteln ist ein vorweihnachtlicher Brauch, bei dem eine Gruppe von Personen auf zufällige Weise Geschenke austauscht. Nimmt man dabei an, dass sich keine Person selbst beschenkt, kann der Austausch der Geschenke mathematisch als fixpunktfreie Permutation der Personen beschrieben werden.

Literatur

Martin Aigner: Diskrete Mathematik. Vieweg, 2006, ISBN 3-8348-0084-8.
Albrecht Beutelspacher, Marc-Alexander Zschiegner: Diskrete Mathematik für Einsteiger. Springer, 2007, ISBN 3-8348-9182-7.
Norbert Henze: Stochastik für Einsteiger. 10. Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-03076-6.
Herbert Kütting, Martin J. Sauer: Elementare Stochastik: Mathematische Grundlagen und didaktische Konzepte. Springer, 2011, ISBN 3-8274-2759-2.
Matthias Löwe, Holger Knöpfel: Stochastik – Struktur im Zufall. Oldenbourg, 2011, ISBN 3-486-70676-4.

Basierend auf einem Artikel in:

Wikipedia.de