Shockley-Gleichung

Die Shockley-Gleichung, benannt nach William B. Shockley, beschreibt die Strom-Spannungs-Kennlinie einer Halbleiterdiode.

Sie lautet nach Wagner:

Kennlinie einer 1N4001-Diode (gilt für 1N4001 bis 1N4007)

$I_{\text{D}}=I_{\text{S}}(T)\,\left(\exp \left({\frac {U_{\text{F}}}{n\,U_{\text{T}}}}\right)-1\right)$

mit

dem Strom $I_{{\text{D}}}$ durch die Diode
dem temperaturabhängigen Sättigungssperrstrom (kurz Sperrstrom) $I_{{\text{S}}}(T)\approx {10^{{-12}}\dots 10^{{-6}}\;{\mathrm {A}}}$
der Anoden-Kathoden-Spannung oder Flussspannung $U_{{\text{F}}}$
dem Emissionskoeffizient $n\approx 1\dots 2$
der Temperaturspannung bei 20 °C
- der absoluten Temperatur
- der Boltzmannkonstante $k_{\mathrm {B} }$
- der Elementarladung .

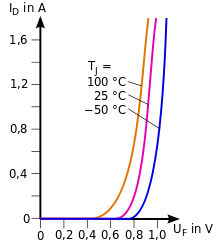
Mit steigender Temperatur steigt auch der Strom durch die Diode; zwar sinkt der Wert der Exponentialfunktion wegen steigender Temperaturspannung, aber dies wird überkompensiert durch die starke Erhöhung des Sperrstroms mit der Temperatur.

In Durchlassrichtung, also für positive Spannung $U_{{\text{F}}}$ , wächst die Exponentialfunktion für Werte von $U_{{\text{F}}}$ , die größer als $n\ U_{{\text{T}}}$ sind, stark an. Damit erhält man für die Shockley-Gleichung in guter Näherung:

$I_{\text{D}}\approx I_{\text{S}}(T)\,\cdot \exp \left({\frac {U_{\text{F}}}{n\,U_{\text{T}}}}\right)$

Für $U_{\text{F}}>n\cdot 120\,\mathrm {mV}$ weicht diese Näherung um weniger als 1 % vom theoretischen Wert ab, für $U_{\text{F}}>n\cdot 180\,\mathrm {mV}$ um weniger als 1 ‰. Wie man an den Kennlinien sieht, ist die tatsächliche Spannung deutlich höher.

Die Shockley-Gleichung beschreibt das Großsignalverhalten, also die physikalisch messbaren Größen einer Diode. Im Kleinsignalverhalten approximiert man die Gleichung durch eine lineare Näherung in der Umgebung eines gewählten Arbeitspunktes.

Basierend auf einem Artikel in:

Wikipedia.de