
Restwelligkeit
Wenn eine Gleichspannung aus sinusförmiger Wechselspannung durch Gleichrichtung entstehen soll, so entsteht immer eine Mischspannung aus Gleich- und überlagerter Wechselspannung. Einfache Schaltungen zur Verminderung des Wechselanteils verwenden einen Glättungskondensator oder eine Glättungsdrossel, oft beides zusammen. Die Tatsache, dass trotz Glättung noch ein (dann meistens unerwünschter) Wechselspannungsanteil bestehen bleibt, wird mit Restwelligkeit bezeichnet. Auch geregelte Netzteile und Schaltnetzteile haben eine, wenn auch wesentlich geringere, Restwelligkeit.
Definitionen
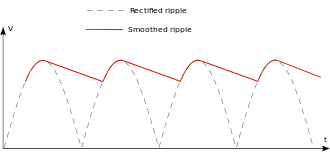
Die nachfolgenden Definitionen gelten in gleicher Weise für elektrische Spannung und Stromstärke. Zur Vereinfachung beschränkt sich dieser Text auf die Spannung.
Eine Mischgröße
setzt sich zusammen aus einem Gleichanteil und einem Wechselanteil
Zur quantitativen Beschreibung des Wechselanteils gibt die hierzu maßgebliche Norm DIN 40110-1 („Wechselstromgrößen“; März 1994) drei Größenverhältnisse an:
- Schwingungsgehalt als Verhältnis Effektivwert
des Wechselanteils
zu Effektivwert der gesamten Mischgröße
- Welligkeit als Verhältnis Effektivwert des Wechselanteils zu Betrag
des Gleichwertes
- Schwankungswelligkeit (Riffelfaktor) als Verhältnis
Schwingungsbreite oder Spitze-Tal-Wert
(früher Spitze-Spitze-Wert
) zu Betrag des Gleichwertes
Der Schwingungsgehalt kann Werte von 0 (bei Gleichspannung) bis 1
(Wechselspannung) bzw. 0 … 100 % annehmen.
Die Welligkeit und die
Schwankungswelligkeit liegen im Bereich 0 (Gleichspannung) … ∞
(Wechselspannung).
Gelegentlich wird statt der Welligkeit
auch ihr logarithmisches
Maß
angegeben.
Nicht in dieser Norm genannt wird die Restwelligkeit .
Sie wird definiert als
Darin ist der Formfaktor
das Verhältnis Effektivwert zu Gleichrichtwert
wobei im vorliegenden Zusammenhang (Spannung ohne Vorzeichenwechsel)
Gleichrichtwert dasselbe ist wie Betrag des Gleichwertes. Mit
stimmt nach elementarer Umrechnung die Definition der Restwelligkeit mit der
oben gegebenen Definition der Welligkeit überein.
Als Kenngröße für die Restwelligkeit wird teilweise nur der Wechselanteil
angegeben als Effektivwert
oder Spitze-Tal-Wert
.
Solche Angaben erfolgen in Millivolt oder Volt.
Literatur
- Andreas Friesecke: Die Audio-Enzyklopädie. Ein Nachschlagewerk für Tontechniker, 2. Auflage, Walter De Gruyter GmbH, Berlin 2014, ISBN 978-3-11-034013-6.
- Theodor Wasserrab: Schaltungslehre der Stromrichtertechnik. Springer Verlag Berlin/Göttingen/Heidelberg, Berlin 1962.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.01. 2024